期望总结

终于理解了一点期望。
定义E(X)：X表示一个随机变量，xi为X的若干种取值，pi表示X取xi的概率。
则E(X)=xi×pi之和。
性质：
E(C)=C （显然，C为常数，仅有一种取值）。

E(X+Y)=E(X)+E(Y) （不要求X和Y独立）。

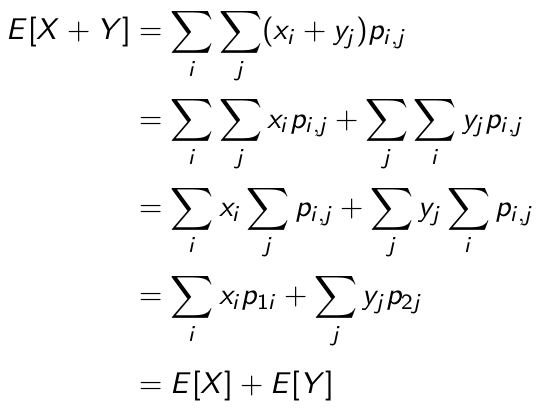
因为不管X，Y是否独立，根据定义，pi1+pi2+....+pim始终等于1，同理，p1j+p2j+....+pnj始终等于1。
这里的X+Y的取值就是X的每一种情况与Y的每一种情况的取值之和。
E(XY)=E(X)*E(Y) （要求X和Y独立）

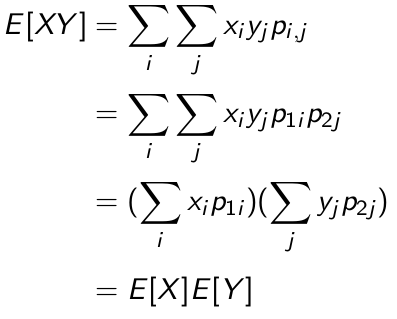
只有X，Y独立时，pij才等于pxi*pyj。
这里的X+Y的取值就是X的每一种情况与Y的每一种情况的取值之积。
证明的本质是用乘法分配律。

连续的还没懂。