点分治总结
点分治
点分治就是基于点的分治。
方法如下:dfs遍历整棵树,在遍历到点u时,考虑LCA为u的点对组成的路径,方法如下:
依次考虑u的所有子节点v,对这些v的子树进行遍历,并考虑每个点与之前遍历的点组成的路径。
这种方法的时间复杂度为\(O(子树大小之和)\)。
但这样对一些极限数据会超时(例如一条链的情况),可能退化到\(O(n^2)\)。
考虑优化:
因为每次考虑点对,都是在以u为根的子树中考虑,与其它节点无关(其他点对的LCA不可能是u)。
所以每次dfs到u时,在处理完u为根的点对后,接下来要考虑u的子节点v,v的子树就相当于是一棵独立的树,所以对于这棵独立的树的dfs可以从任意节点开始继续搜索。为了让效率尽量高,我们应当选取树的重心作为根。
可以证明,这样的最坏时间复杂度为\(O(nlogn)\)
树的重心也叫树的质心。对于一棵树n个节点的无根树,找到一个点,使得把树变成以该点为根的有根树时,最大子树的结点数最小。换句话说,删除这个点后最大连通块(一定是树)的结点数最小。
如图:
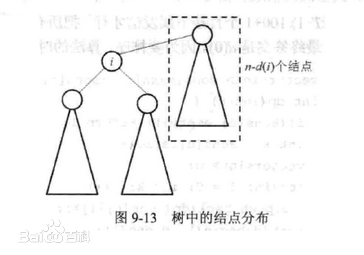
找重心可以一遍dfs得出。
例题1
洛谷P4149 [IOI2011]Race
求树中长度为K,且经过边数最少的路径。\((K \leq 10^6)\)
思路:
开一个数组,记录长度为\(i\)的路径的最少边数,遍历到长度为\(i\)的路径时,查询长度为\(K-i\)的路径。
清数组不能暴力,要开一个栈,记录所有修改,再针对这些修改清空。
代码
#include <stdio.h>
int fr[200010],ne[400010];
int v[400010],w[400010],bs=0;
void addb(int a,int b,int c)
{
v[bs]=b;
w[bs]=c;
ne[bs]=fr[a];
fr[a]=bs;
bs+=1;
}
int mi,wz,dx[200010];
bool bk[200010]={0};
void getroot(int u,int f,int sl)
{
dx[u]=1;
int ma=-1;
for(int i=fr[u];i!=-1;i=ne[i])
{
if(v[i]==f||bk[v[i]])
continue;
getroot(v[i],u,sl);
if(dx[v[i]]>ma)
ma=dx[v[i]];
dx[u]+=dx[v[i]];
}
if(sl-dx[u]>ma)
ma=sl-dx[u];
if(ma<mi)
{
mi=ma;
wz=u;
}
}
int zx[1000010],xg[200010],cd[200010],gs,K,jg,inf=99999999;
void dfs2(int u,int f,int jl,int b)
{
if(jl<=K)
{
xg[gs]=jl;
cd[gs++]=b;
if(zx[K-jl]+b<jg)
jg=zx[K-jl]+b;
}
else
return;
for(int i=fr[u];i!=-1;i=ne[i])
{
if(v[i]==f||bk[v[i]])
continue;
dfs2(v[i],u,jl+w[i],b+1);
}
}
void solve(int u)
{
gs=0;
for(int i=fr[u];i!=-1;i=ne[i])
{
if(bk[v[i]])
continue;
int la=gs;
dfs2(v[i],u,w[i],1);
for(int i=la;i<gs;i++)
{
if(cd[i]<zx[xg[i]])
zx[xg[i]]=cd[i];
}
}
for(int i=0;i<gs;i++)
{
if(xg[i]==K&&zx[xg[i]]<jg)
jg=zx[xg[i]];
zx[xg[i]]=inf;
}
}
int dfs3(int u,int f)
{
int rtn=1;
for(int i=fr[u];i!=-1;i=ne[i])
{
if(v[i]!=f&&!bk[v[i]])
rtn+=dfs3(v[i],u);
}
return rtn;
}
void dfs1(int u)
{
bk[u]=true;
solve(u);
for(int i=fr[u];i!=-1;i=ne[i])
{
if(bk[v[i]])
continue;
mi=inf;
getroot(v[i],u,dfs3(v[i],u));
dfs1(wz);
}
}
int main()
{
int n;
scanf("%d%d",&n,&K);
for(int i=0;i<n;i++)
fr[i]=-1;
for(int i=0;i<n-1;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
addb(a,b,c);
addb(b,a,c);
}
jg=mi=inf;
for(int i=0;i<=1000000;i++)
zx[i]=inf;
getroot(0,-1,n);
dfs1(wz);
if(jg==inf)
printf("-1");
else
printf("%d",jg);
return 0;
}
例题2
[BJOI2017]树的难题
将每个点的子树按颜色排序,并使用线段树维护最大权值。
时间复杂度\(O(n\log ^2n)\)
\(n\leq2*10^5\),时限2秒,会卡常。
考虑如下常数优化:
由于边权为1,所以计算每棵子树时,最大的长度就是这个节点到叶子结点的最长链长度(设为m)。
在计算时,将线段树重建,范围为0~m。
这样,查询时的复杂度就会小一些,变成\(O(\log m)\)。
并且无需在最后清空线段树,直接重建时清空就行了。
这样就能过了。
代码:
#include <stdio.h>
#include <stdlib.h>
int fr[200010],ne[400010],n;
int v[400010],w[400010],bs=0;
int C[200010];
int inf=999999999;
#define re register
inline int max(int a,int b)
{
return a>b?a:b;
}
void addb(int a,int b,int c)
{
v[bs]=b;
w[bs]=c;
ne[bs]=fr[a];
fr[a]=bs;
bs+=1;
}
struct SXds
{
int zd[800010],sz[200010];
void jianshu(re int i,re int l,re int r)
{
zd[i]=-inf;
if(l+1==r)
{
sz[l]=-inf;
return;
}
int m=(l+r)>>1;
jianshu(i<<1,l,m);
jianshu((i<<1)|1,m,r);
}
void pushup(int i)
{
zd[i]=zd[(i<<1)|1];
if(zd[i<<1]>zd[i])
zd[i]=zd[i<<1];
}
void xiugai(re int i,re int l,re int r,re int j,re int x)
{
if(l+1==r)
{
zd[i]=sz[j]=x;
return;
}
re int m=(l+r)>>1;
if(j<m)
xiugai(i<<1,l,m,j,x);
else
xiugai((i<<1)|1,m,r,j,x);
pushup(i);
}
int chaxun(re int i,re int l,re int r,re int L,re int R)
{
if(r<=L||R<=l)
return -inf;
if(L<=l&&r<=R)
return zd[i];
re int m=(l+r)>>1;
re int t1=chaxun(i<<1,l,m,L,R),t2=chaxun((i<<1)|1,m,r,L,R);
if(t2>t1)
t1=t2;
return t1;
}
};
SXds xt,bt;
bool bk[200010];
int dfs1(re int u,re int f)
{
int rt=1;
for(re int i=fr[u];i!=-1;i=ne[i])
{
if(v[i]!=f&&!bk[v[i]])
rt+=dfs1(v[i],u);
}
return rt;
}
int mi=inf,wz;
int dfs2(re int u,re int f,re int si)
{
int zd=-1,rt=1;
for(re int i=fr[u];i!=-1;i=ne[i])
{
if(v[i]!=f&&!bk[v[i]])
{
int t=dfs2(v[i],u,si);
rt+=t;
if(t>zd)
zd=t;
}
}
if(si-rt>zd)
zd=si-rt;
if(zd<mi)
{
mi=zd;
wz=u;
}
return rt;
}
int st[200010],qz[200010],cd[200010],tp=0,jg=-inf,cl,cr;
struct SPx
{
int z,u;
};
SPx px[200010];
int cmp(const void*a,const void*b)
{
return ((SPx*)a)->z-((SPx*)b)->z;
}
int zc;
void dfs5(int u,int f,int sd)
{
if(sd>zc)
zc=sd;
for(int i=fr[u];i!=-1;i=ne[i])
{
if(v[i]!=f&&!bk[v[i]])
dfs5(v[i],u,sd+1);
}
}
void dfs3(re int u,re int f,re int co,re int la,re int he,re int jl)
{
qz[u]=he+C[la];
cd[u]=jl;
st[tp++]=u;
re int t=xt.chaxun(1,0,zc,cl-jl,cr-jl+1)+he-C[co]+C[la];
if(t>jg)
jg=t;
t=bt.chaxun(1,0,zc,cl-jl,cr-jl+1)+he+C[la];
if(t>jg)
jg=t;
for(re int i=fr[u];i!=-1;i=ne[i])
{
if(v[i]!=f&&!bk[v[i]])
dfs3(v[i],u,co,w[i],(w[i]==la?he:he+C[la]),jl+1);
}
}
void solve(int u)
{
re int sl=0;
for(re int i=fr[u];i!=-1;i=ne[i])
{
if(!bk[v[i]])
{
px[sl].u=v[i];
px[sl++].z=w[i];
}
}
qsort(px,sl,sizeof(SPx),cmp);
tp=0;
re int la,lx=0;
zc=-inf;
dfs5(u,-1,0);
zc+=1;
xt.jianshu(1,0,zc);
bt.jianshu(1,0,zc);
bt.xiugai(1,0,zc,0,0);
for(re int i=0;i<sl;i++)
{
la=tp;
if(i>0&&px[i].z!=px[i-1].z)
{
for(re int j=lx;j<tp;j++)
{
xt.xiugai(1,0,zc,cd[st[j]],-inf);
if(qz[st[j]]>bt.sz[cd[st[j]]])
bt.xiugai(1,0,zc,cd[st[j]],qz[st[j]]);
}
lx=tp;
}
dfs3(px[i].u,u,px[i].z,px[i].z,0,1);
for(int j=la;j<tp;j++)
{
if(qz[st[j]]>xt.sz[cd[st[j]]])
xt.xiugai(1,0,zc,cd[st[j]],qz[st[j]]);
}
}
}
void dfs4(int u)
{
bk[u]=true;
solve(u);
for(int i=fr[u];i!=-1;i=ne[i])
{
if(!bk[v[i]])
{
mi=inf;
int si=dfs1(v[i],u);
dfs2(v[i],u,si);
dfs4(wz);
}
}
}
int main()
{
int m;
scanf("%d%d%d%d",&n,&m,&cl,&cr);
for(int i=1;i<=n;i++)
fr[i]=-1;
for(int i=1;i<=m;i++)
scanf("%d",&C[i]);
for(int i=0;i<n-1;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
addb(a,b,c);
addb(b,a,c);
}
mi=inf;
dfs2(1,-1,n);
dfs4(wz);
printf("%d",jg);
return 0;
}



