后缀自动机总结
概念
后缀自动机,是一个能识别一个字符串的所有后缀的自动机。
考虑一种最简单的实现:
将一个字符串的所有后缀插入到一棵trie中。
如图:
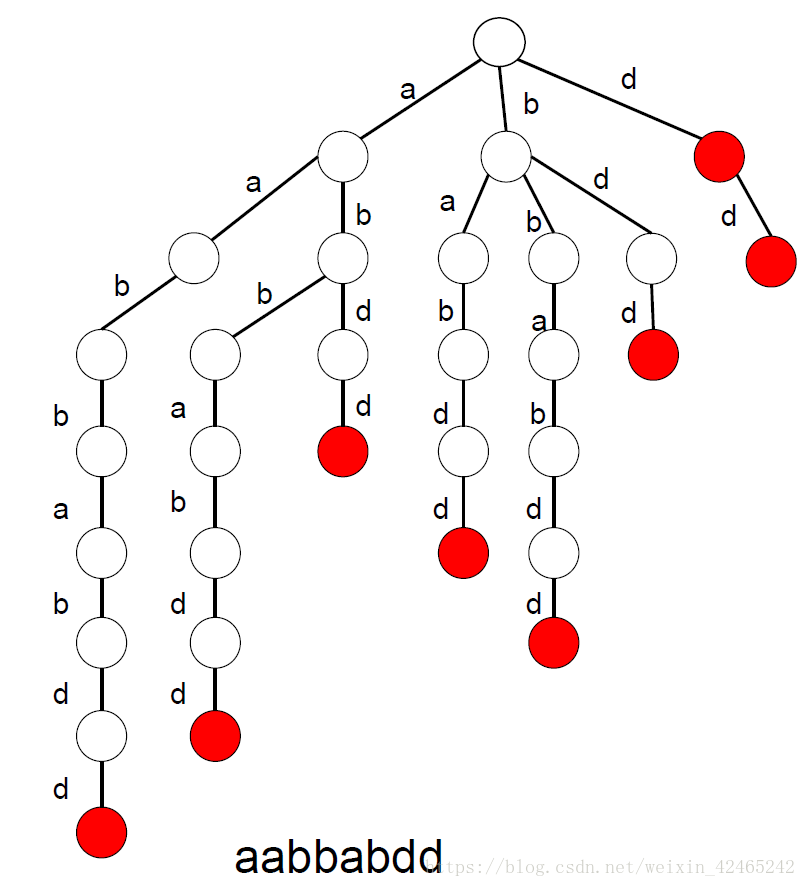
可以发现后缀树每个点对应一个后缀集合,每个点对应的后缀集合是这个点子树中所有结束节点所表示的后缀的集合。
把每个点对应的后缀集合称为righ(x)
由于一个字符串的本质不同子串是\(O(n^2)\)级别的,因此后缀树的节点数是\(O(n^2)\)级别的。
考虑优化:
首先,给每个结点添加trs指针,表示在一个字符串前加一个字符能转移到的结点。
pre指针表示在前面去掉一个字符转移到的节点。
如图:
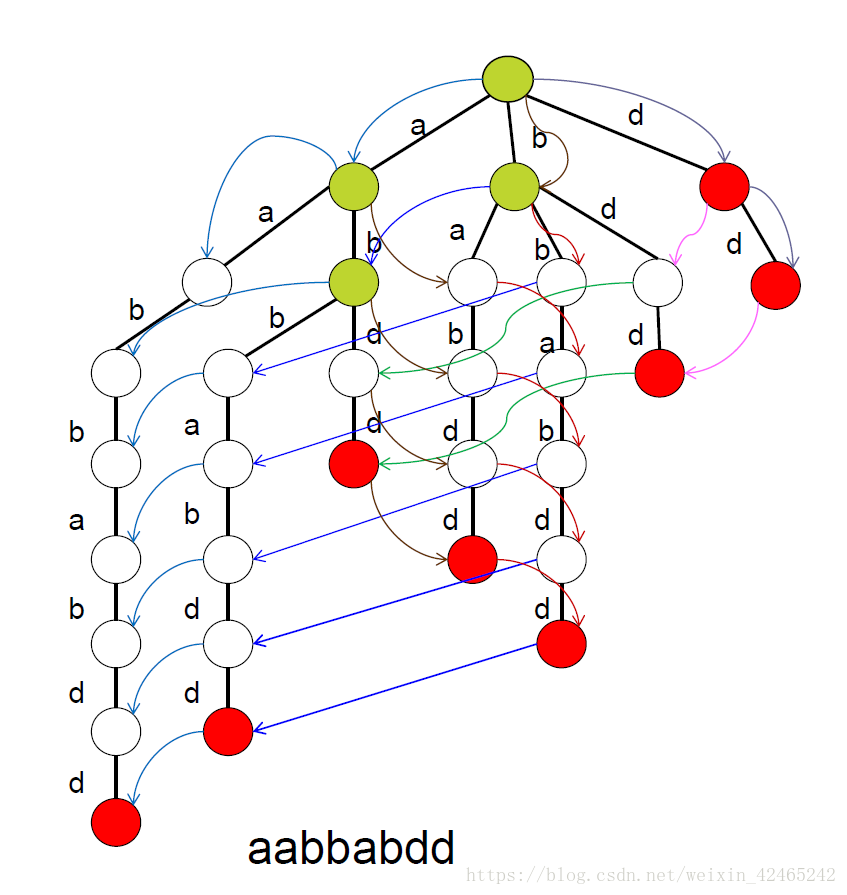
结束节点用红色标出,有一个以上儿子的节点用绿色标出,即使根只有一个儿子也将根标记为绿色。
我们把所有白点以及他的指针压缩到下面最近的一个有色点,这样我们就得到了这个串的后缀自动机。
红点的pre一定是红点,因为后缀的前面去掉一个字符后仍然是后缀。
绿点的pre一定是绿点,因为原来有一个分支,去掉后仍然有分支。
所以,白点的trs一定是白点。
可以发现,每个有色点和上面一段白点trs的存在性是相同的。并且这些白点trs到达的结点在压缩之后都相同。
所以,在匹配过程中,这些白点就可以看作相同的,压缩为一个点后不会对结果产生影响。
可以理解为白点仍然存在,只不过为了节省空间,被隐藏了。(也可以了理解为建出红点的虚树)。
可以发现,红点有n个,绿点相当于每次把若干个红点集合合并,最多合并n次就会变成一个集合。
所以压缩之后点数是\(O(n)\)的。可以证明,边数也是\(O(n)\)的。
其实就是暴力后缀trie的每个后缀的虚树。
现在考虑如何构造这个后缀自动机。
对于每个结点,保存它在压缩后的树中的父结点,它对应串的长度 (只保留这一段被压缩的点中,最下面的点(即有色点)的长度),以及它的trs。
下文中的“对应的字符串”均指这一段被压缩的点中,最下面的点对应的字符串。
构造
使用增量构造法:假设当前已经建出了关于字符串S的后缀自动机,考虑构建关于字符串cS的后缀自动机。
设last为上一次构造的结尾,np为当前构造后的结尾。
分三种情况讨论:
情况1:
根不存在为c的儿子。
这种情况,说明若将cS插入后缀树,将变为如下情况:
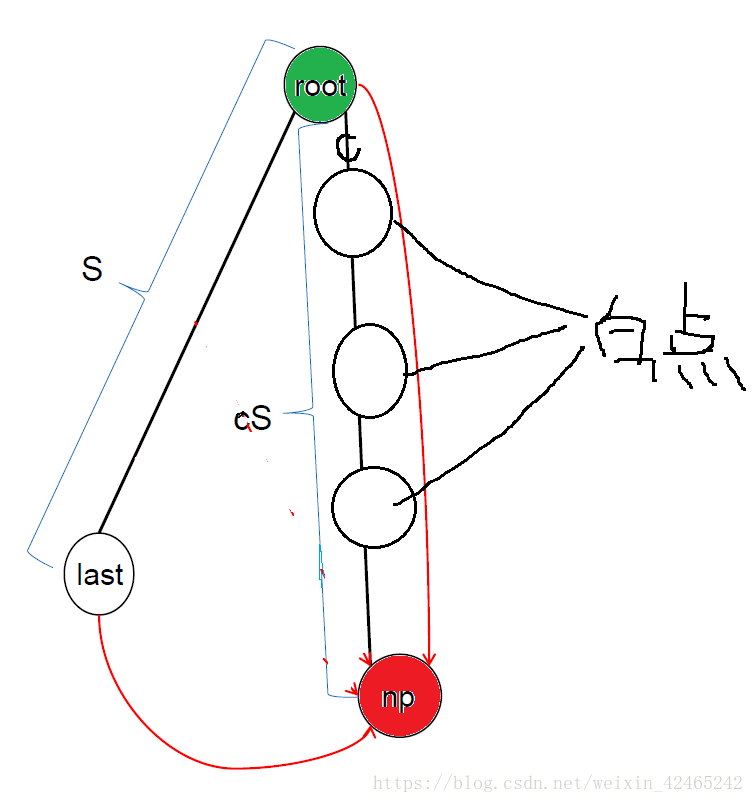
添加trs指针后:
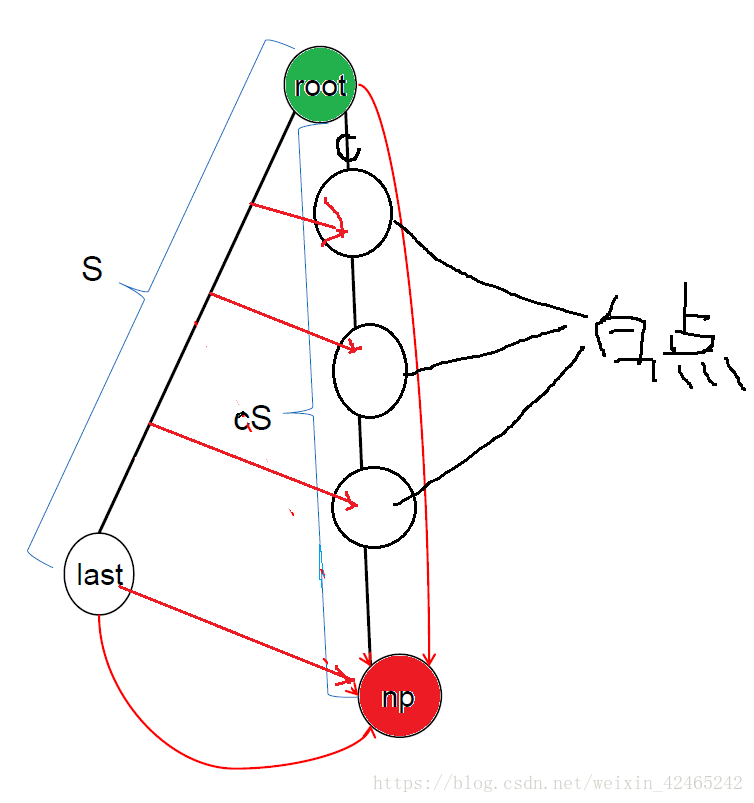
压缩后:
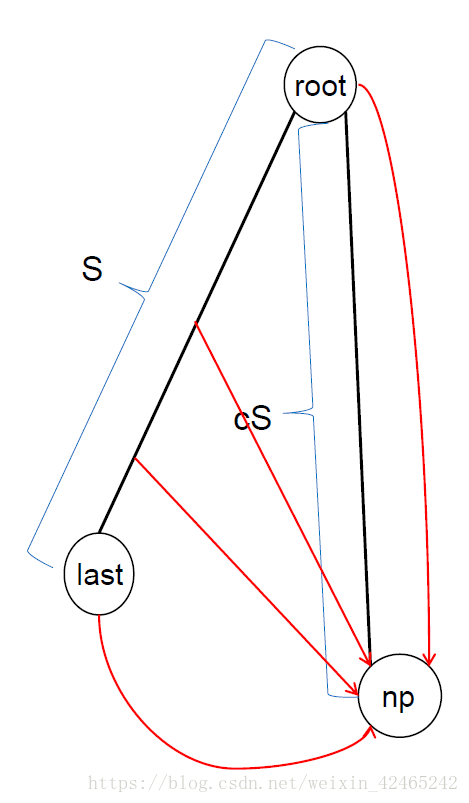
(这里忽略的点的颜色)
就是说,如果根不存在为c的儿子,即last及他的祖先中没有trs( c )的指针,那么可以直接给根加一个np的儿子。
对于trs指针,只需要把last到根的所有trs( c )赋成np就行了。
情况2:
根存在为c的儿子。
找到last第一个存在trs( c )的祖先p(一定存在这样的祖先,因为根存在trs( c )),然后将从last到p以下的部分的trs( c )赋成np。(原因同情况1,因为这些trs( c )在p下面,np上面,这些点一定是白点,压缩后都会变成np)。
设q=trs(p,c),此时有两种情况:
1
\(len[q]=len[p]+1\)
如图:
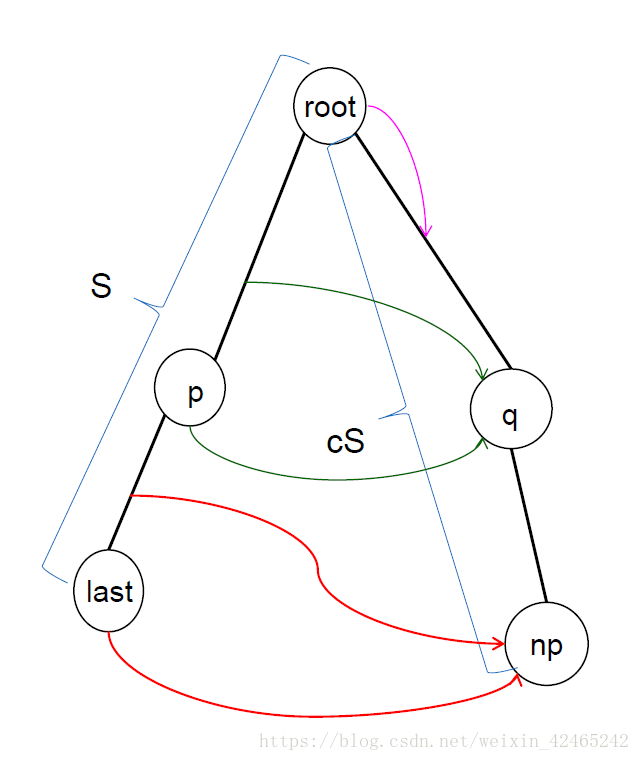
说明q是一个有色点,即q对应的字符串是cp。由于p是last的祖先,所以p是S的前缀,所以cp是cS的前缀。所以root到q是np的一个前缀。
因此只需要把np接在q的下面,对于trs指针无需做其他修改。
2
\(len[q]!=len[p]+1\)
这说明,q对应的字符串并不是cp,而cp是一个被压缩到q上的白点。
设这个白点为nq,则q变为nq的儿子。
现在,root到q不是np的一个前缀。
证明:假设root到q是np的一个前缀,那q的pre一定在last到p的路径上,由于last到p以下的点没有trs( c ),所以假设不成立。
所以,root到q不是np的一个前缀。
因此nq是一个分叉点(绿点)。需要把这个点新建出来。
nq的父亲指向q原来的父亲,q和np的父亲指向nq。
此时trs(p,c)应指向nq,并且p祖先的trs( c )如果原来指向q,现在应指向nq。
原因:既然trs(p,c)指向q,所以p祖先的trs( c )指向的应该是q的祖先。
若p祖先的trs( c )原来指向q,说明它实际指向q上面的一个白点(且原来下面最近的一个有色点是q)。
新建nq后,这个白点下面最近的一个有色点就变为了nq,所以现在应指向nq。
并且,trs( c )原来指向q的p的祖先,一定是一段连续的节点。
因为trs( c )!=q,就说明下面又出现了一个新的有色点,而再往祖先走,下面还有这个有色点,所以trs( c )不可能变为q。
新建nq后,这个白点下面最近的一个有色点就变为了nq。
所以这些trs现在应指向nq。
因为nq原来是一个q的白点,因此nq的trs与q相同。只需要将q的trs赋给nq。
如图:
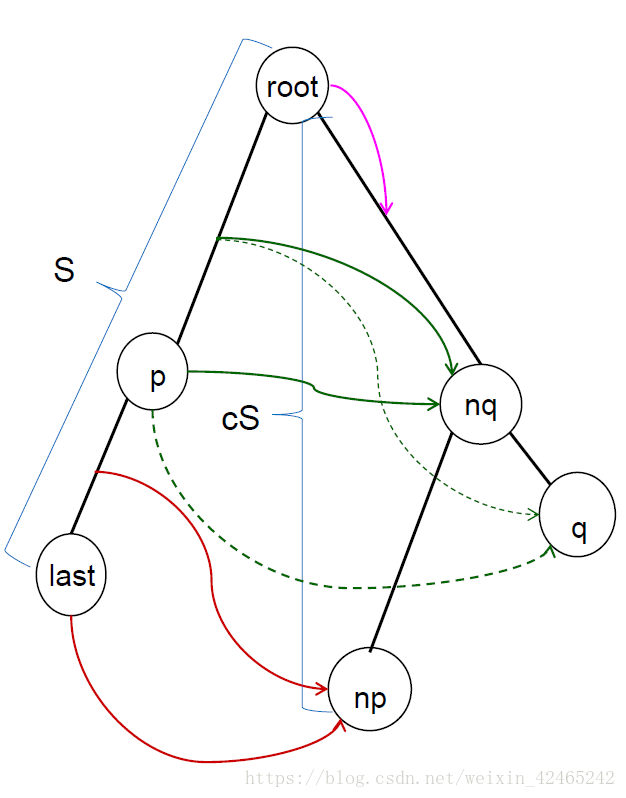
代码:
void insert(int c)
{
int np=++sl,p=la;
len[np]=len[la]+1,la=np;
while(p!=0&&trs[p][c]==0)
{
trs[p][c]=np;
p=fa[p];
}
if(p==0)//情况1
fa[np]=1;
else
{
int q=trs[p][c];
if(len[q]==len[p]+1)//情况2
fa[np]=q;
else//情况3
{
int nq=++sl;
len[nq]=len[p]+1;
fa[nq]=fa[q];
fa[np]=fa[q]=nq;
for(int i=0;i<26;i++)
trs[nq][i]=trs[q][i];
while(p!=0&&trs[p][c]==q)//一定是区间
{
trs[p][c]=nq;
p=fa[p];
}
}
}
red[np]=true;//标记为后缀树上的红点
}
使用方法
对于这种建树方法,在建树时要从前向后,查询时也从前向后,相当于建一个反串的后缀自动机。
同时注意点数要开到二倍。
按照定义,走trs指针相当于在前面添加一个字符,走fa指针相当于在后面去掉一些字符(压缩的原因)。
因为建的是反串的后缀自动机,所以走trs指针相当于在后面添加一个字符,走fa指针相当于在前面去掉一些字符。
所以,子串能够匹配的集合求法:在fa数组构成的树上,进行遍历,right集合就是子树中红点的集合。
因为在fa数组构成的树上向子树中走,就相当于在前面添加字符,而红点其实对应前缀的集合(因为是反串)。
由于有时求的是所有匹配的信息(即子树信息),因此经常与线段树合并,或DFS序+线段树一起使用
定位子串的快速算法:倍增定位,方法如下:
先找到子串的前缀的位置,再走fa边,就是不停的在前面去掉字符,直到找到子串。
这个过程可以基于长度,树上倍增实现。
fa构成的树:
注意:有时,使用此树时在建树时要从后向前,建原串的后缀自动机。
优点:是一棵树,会方便一些操作。
缺点:有压缩,一条边上有很多字符,比较麻烦。
trs构成的DAG:
优点:没有压缩,容易实现某些操作。
缺点:是DAG,一些操作难以实现。
后缀自动机,在匹配等概念上,把所有子串分为了\(O(n)\)种,每种子串有多个,但在匹配等意义上相同,可以方便的快速枚举所有子串。
广义后缀自动机
如果有多个串,可以在其中添加分隔符实现(但比较费空间)。
如果这种方法不能使用,可以使用广义后缀自动机。
广义后缀自动机和普通自动机的区别体现在如果带插入的串已经存在时的处理。
当待插入串不存在时广义后缀自动机和普通自动机处理方法相同。
并且广义后缀自动机在插入每个串前需要把last赋为1。
int insert(int c)
{
if(trs[la][c])
{
int p=la,q=trs[p][c];
if(len[q]==len[p]+1)
la=q;
else
{
int nq=++sl;
fa[nq]=fa[q];la=nq;
fa[q]=nq;len[nq]=len[p]+1;
for(int i=0;i<26;i++)
trs[nq][i]=trs[q][i];
while(p!=0&&trs[p][c]==q)
{
trs[p][c]=nq;
p=fa[p];
}
}
}
else //同普通后缀自动机
}
例题
例题1
【模板】后缀自动机
建出后缀自动机,求出right集合大小,用len*size更新结果即可。
代码:
#include <stdio.h>
#include <stdlib.h>
int fa[2000010],trs[2000010][26],len[2000010],sl=1,la=1;
int fr[2000010],ne[2000010],qz[2000010];
int v[2000010],bs=0;
bool red[2000010];
void addb(int a,int b)
{
v[bs]=b;
ne[bs]=fr[a];
fr[a]=bs;
bs+=1;
}
void insert(int c)
{
int np=++sl,p=la;
len[np]=len[la]+1,la=np;
while(p!=0&&trs[p][c]==0)
{
trs[p][c]=np;
p=fa[p];
}
if(p==0)
fa[np]=1;
else
{
int q=trs[p][c];
if(len[q]==len[p]+1)
fa[np]=q;
else
{
int nq=++sl;
len[nq]=len[p]+1;
fa[nq]=fa[q];
fa[np]=fa[q]=nq;
for(int i=0;i<26;i++)
trs[nq][i]=trs[q][i];
while(p!=0&&trs[p][c]==q)
{
trs[p][c]=nq;
p=fa[p];
}
}
}
red[np]=true;
}
int si[2000010];
int dfs(int u)
{
if(red[u])
si[u]=1;
for(int i=fr[u];i!=-1;i=ne[i])
si[u]+=dfs(v[i]);
return si[u];
}
char ch[1000010];
int main()
{
scanf("%s",ch);
for(int i=0;ch[i]!=0;i++)
insert(ch[i]-'a');
for(int i=1;i<=sl;i++)
fr[i]=-1;
for(int i=1;i<=sl;i++)
addb(fa[i],i);
dfs(1);
long long ma=0;
for(int i=1;i<=sl;i++)
{
if(si[i]>1)
{
long long t=len[i];
t*=si[i];
if(t>ma)
ma=t;
}
}
printf("%lld",ma);
return 0;
}
例题2
例题3
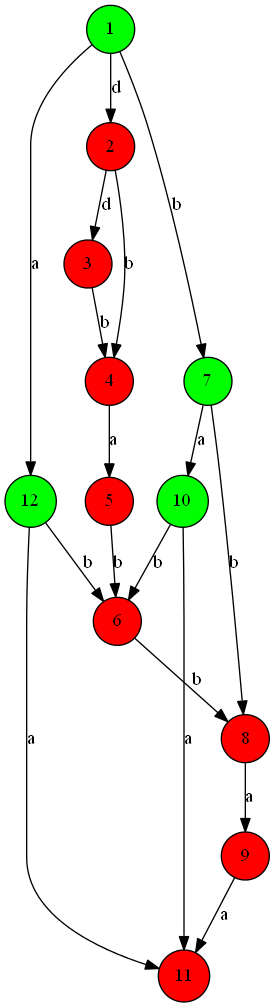
后缀自动机图例:
ddbabbaa: