ABC G Ex 简要题解

ABC212G Power Pair

推柿子题

\(\sum\limits_{x}^{P-1}\sum\limits_{y}^{P-1} \exists n \in \mathbb{N}\ x^n \equiv y(\bmod P)\)

\(1+\sum\limits_{x=1}^{P-1}\sum\limits_{y=1}^{P-1} \exists n \in \mathbb{N}\ x^n \equiv y(\bmod P)\)

考虑模 \(P\) 意义下的原根 \(g\) ,有 \(x=g^a,y=g^b\)

\(1+\sum\limits_{x=1}^{P-1}\sum\limits_{y=1}^{P-1} g^{an} \equiv g^{b} (\bmod P)\)

\(1+\sum\limits_{x=1}^{P-1}\sum\limits_{y=1}^{P-1} an \equiv b (\bmod P-1)\)

这个可以看成一个长度为 \(P-1\) 的环，我每次在上面走 \(a\) 步，求 \(b\) 的数量，这个是 \(\frac{P-1}{\gcd(a,P-1)}\) 个。

\(1+\sum\limits_{a=1}^{P-1}\frac{P-1}{\gcd(a,P-1)}\)

\(1+\sum\limits_{d|(P-1)} \frac{P-1}{d}\sum\limits_{a=1}^{P-1}[\gcd(a,P-1)=d]\)

\(1+\sum\limits_{d|(P-1)} \frac{P-1}{d}\varphi(\frac{P-1}{d})\)

现在就可以求了

\(1e12\) 以内的约数数最多的数有 \(6720\) 个约数，跑不满

code

ABC212H Nim Counting

可以说只要会 \(FWT\) 就可以切

题意：给定长度为 \(K\) 的数组 \(A\) ，给定 \(N\) ，现在你要选择有 \([1,N]\) 堆石子，每一堆石子的数量 \(\in A\) ，现在玩 \(nim\) 游戏，求先手获胜的局面有多少种

其实就是满足在 \(x^a \times x^b=x^{a\ xor \ b}\) 下求 \([x^t]\sum\limits_{i=1}^{n}(f(x))^i\) 其中 \(t \in [1,值域]\)

因为 \(FWT(A+B)=FWT(A)+FWT(B),FWT(A\ xor \ B)=FWT(A) \times FWT(B)\)

所以可以首先先 \(FWT\) ,然后对 \(FWT\) 的每一项做 \(\sum\limits_{i=1}^{n}{a_x}^i=\frac{{a_x}^{n+1}-a}{a-1}\)，然后 \(IFWT\)

code

ABC213G Connectivity 2

小清新计数题

看数据范围考虑状压

设 \(f_S\) 表示现在与一联通的子图点集是 \(S\) 的方案数，转移发现不好转移，所以正难则反，用总数减去不合法

code（这里 \(f\) 为了卡常没有点 \(1\)

ABC214G Three Permutations

个人感觉非常困难

详细写了题解

ABC214H Collecting

洛谷题解全是扯淡的

首先发现可以直接建图流，但是这样时间复杂度是 \(O(nmk)\) 的，\(\%114514\) 过不了，考虑优化

发现有一个东西是 \(Dijsktra\) 求最小费用流，时间复杂度是 \(O(nm+km\log m)\) 的，时间复杂度瓶颈在一开始要求一遍 \(spfa\) ，考虑怎么建出来图没有负权边，之前的建图要建负权边是因为我要求的是最大费用最大流，发现这玩意就是最小浪费代价最大流，这玩意要怎么弄呢，首先缩点成为一个 \(dag\) ，按 \(dag\) 层数标号，我要是从一个编号为 \(i\) 的点到一个编号为 \(j\) 点的话中间的肯定选不上，要是走到这里就不走了说明后面的全选不了，这样就可以做了

code

ABC215G Colorful Candies 2

挺傻逼的一道题

但是我降智没想出来/ng

退役算了/cf

假设现在有 \(m\) 种颜色，你选 \(x\) 个球，那么选颜色 \(i\) 的概率就是 \(\frac{{n \choose x} - {n-sum_i \choose x}}{n \choose x}\)

这样就可以 \(O(n^2)\) 了

然后发现本质不同的 \(sum_i\) 个数时 \(\sqrt n\) 级别的，所以可以 \(O(n\sqrt n)\) 做了

ABC215H Cabbage Master

学习到的很多

很容易联想到二分图，每一个球是左部点，每一个盒子是右部点（当然做的时候不用建出来，不然就寄了，所以下面说的左部点都是对于颜色，右部点都是对于盒子），求完美匹配

考虑霍尔定理

\(n<=20\) 可以直接枚举，但是发现右部点的权值不好算，所以可以改一下枚举的定义，即我选了一些右部点，他们所有可达的左部点集合为 \(S\) ，这样就可以 \(FWT\) 算右部点权值了

假设现在我选的左部点权值是 \(x\) ，右部点权值是 \(y\) ,第一问答案就是 \(cnt=min\{y-x+1\}\)

将不用删点特判掉之后考虑求方案数

当一个左部点集合 \(S\) 删去 \(cnt\) 个点时没有完美匹配当且仅当 \(\exists \ T \ S \in T\) 且 \(T\) 的 \(y-x+1=cnt\) ，为了不算重，我们钦定 \(S\) 里面包含的颜色都至少被删去一个球。

至于怎么求，考虑容斥

先提前算出不钦定的值，然后外层枚举现在处理到第几个颜色，内层枚举集合 \(S\) 现在等于时颜色编号小于 \(S\) 的都已经钦定选了，然后你减去把现在枚举的颜色去掉的 \(dp\) 值，仔细想想发现很正确

code

ABC219H Candles

可能？是套路题

但是我不会/ng

因为我不能记时间，所以可以考虑费用提前计算

首先先思考假如蜡烛可以燃烧到负数，发现这就是 P1220 关路灯 ，但是现在不能燃烧到负数，也就是 \(\max(0,a_i)\) ，于是就有一个思路就是在第 \(i\) 根蜡烛的时候把 \(a_i\) 和 \(0\) 都转移一遍，因为是取 \(\max\) ，所以最后答案是正确的

现在我不知道有多少蜡烛是没到就会燃尽，所以我区间 \(dp\) 多记一维表示当前区间外有 \(i\) 根蜡烛未燃尽，这样就可以实现上述转移了

设 \(f_{l,r,i,0/1}\) 表示在区间 \([l,r]\) ，区间外有 \(i\) 根蜡烛在燃烧，现在在 左/右 端点时的燃烧掉的最小值

\(f_{l,r+1,i,0}=\min\{f_{l,r,i,0/1}+i \times dist+a_{r+1},f_{l,r,i+1,0/1}+i \times dist\}\) 其他转移同理

\(\min\) 中前面的就是 \(r+1\) 的熄灭了，后面的时没熄灭的

code

ABC230G GCD Permutation

糗大了，做法是个傻逼玩意

直接推柿子。

题目要求：

\[\sum_{i=1}^{n}\sum_{j=i}^{n}[\gcd(i,j)\neq1][\gcd(P_i,P_j)\neq1] \]

有 \(\gcd​\) ，考虑莫比乌斯反演，发现莫比乌斯反演好像只能做 \(\gcd(i,j)=1​\) ，所以先推一下 \(\sum\limits_{i=1}^{n}\sum\limits_{j=i}^{n}[\gcd(i,j)=1][\gcd(P_i,P_j)=1]​\) 其实是我一开始看错题了。

首先将 \([\gcd(i,j)=1]​\) 莫比乌斯反演一下：

\[\begin{eqnarray} &\sum_{i=1}^{n}&\sum_{j=i}^{n}[\gcd(i,j)=1][\gcd(P_i,P_j)=1] \\ =&\sum_{d=1}^{n}&\mu(d)\sum_{d\mid i}^{n}\sum_{d\mid j}^{n}[\gcd(P_i,P_j)=1][i \le j] \\ \end{eqnarray} \]

然后将 \([\gcd(P_i,P_j)=1]\) 反演一下：

\[\begin{eqnarray} &\sum_{d=1}^{n}&\mu(d)\sum_{k=1}^{n}\mu(k)\sum_{d\mid i,k\mid P_i}^{n}\sum_{d\mid j,k \mid P_j}^{n}[i \le j] \\ =&\sum_{d=1}^{n}&\mu(d)\sum_{k=1}^{n}\mu(k)\ \frac{sum(d,k) (sum(d,k)+1)}{2} \\ \end{eqnarray} \]

其中 \(sum(d,k)\) 表示 \(d \mid i,k \mid P_i\) 的 \(i\) 的个数。

不难发现对于每一个数 \(i\) 最多只会对 \(sum\) 数组贡献 \(\log^2\) 次，因为约数个数是 \(\log\) 级别的，所以时间复杂度 \(O(n\log^2 n)\)。

现在已经会做 \(\sum\limits_{i=1}^{n}\sum\limits_{j=i}^{n}[\gcd(i,j)=1][\gcd(P_i,P_j)=1]\) ，考虑怎么转化回题目本身，考虑莫比乌斯反演的本质是依靠 \(\sum\limits_{d \mid n}\mu(d)=[n=1]\) 这个柿子搞的，现在我们要求的是跟这个正好相反的柿子，也就是说只要构造出来一个函数 \(\xi(i)\) 满足 \(\sum\limits_{d \mid n}\xi(d)=[n\neq1]\) 就可以了，这个很好构造，考虑 \(\mu\) 的定义：

\[\mu(i) = \begin{cases} 1 \quad n = 1 \\ 0 \quad \text{ $i$ 含有质因子平方}\\ (-1)^k \quad \text{ $k$ 为 $i$ 的质因子个数} \end{cases} \]

首先因为 \(n=1\) 时要求 \(\xi(n)=0\) ，所以：

\[\xi(i) = \begin{cases} 0 \quad n = 1 \\ \end{cases} \]

然后考虑为什么当 \(n\neq1\) 时 \(\mu(i)=0\) ，假设 \(n\) 有 \(k\) 个质因子，根据定义 \(\sum\limits_{d\mid n}^{n}\mu(d)=\sum\limits_{i=0}^{k}(-1)^i{k \choose i}\) ，因为有平方因子贡献为 \(0\) ，所以直接枚举有几个因子就可以了。

把平方质因子搞掉这个性质很好，我们可以借鉴过来，也就是我们还是不要平方因子，现在的规则就是：

\[\xi(i) = \begin{cases} 0 \quad n = 1 \\ 0 \quad \text{ $i$ 含有平方因子}\\ \end{cases} \]

现在就是只要构造出 \(f_i​\) 满足 \(\sum\limits_{i=1}^{k}f_i{k \choose i}=1​\) 就可以了，还是借鉴莫比乌斯函数，发现 \(\sum\limits_{i=1}^{k}(-1)^k{k \choose i}=-1​\) ，所以我们直接取反就好了。

也就是现在的规则是：

\[\xi(i) = \begin{cases} 0 \quad n = 1 \\ 0 \quad \text{ $i$ 含有质因子平方}\\ (-1)^{k-1} \quad \text{ $k$ 为 $i$ 的质因子个数} \end{cases} \]

现在我们已经构造出 \(\xi\) 了，只要将上面推出来的柿子中的 \(\mu\) 换成 \(\xi​\) 就好了。

code

ABC298Ex - Sum of Min of Length

挺神秘的一道题

题意：给你一棵树，多次询问，每次询问给定两个点 \(x,y\)，求 \(\sum\limits_{u=1}^{n} \min(dist(u,x),dist(u,y))\)

如果只有一个点发现非常好求，直接换根 \(dp\) 就好了，现在考虑两个点怎么做

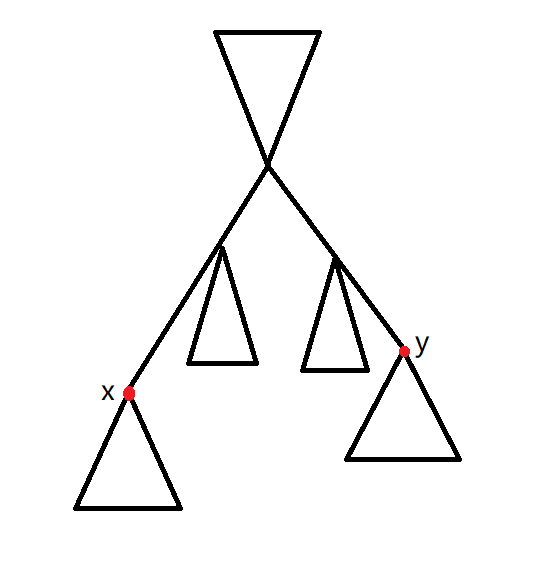
首先肯定是要找出 \(u\) 到 \(v\) 的中点 \(mid\) 的

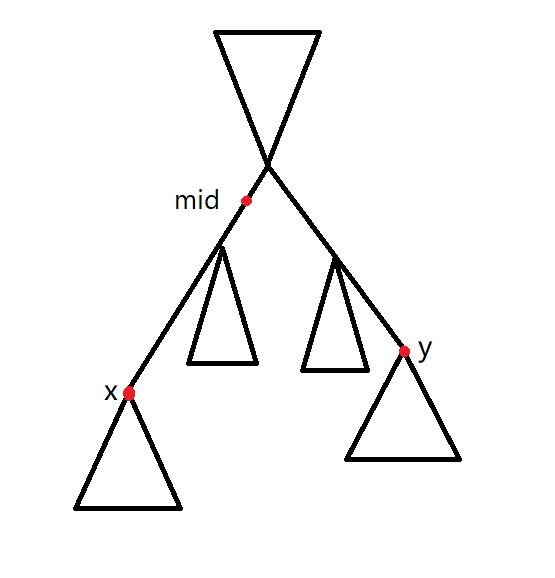
其中以 \(mid\) 为子树的点肯定是到 \(u\) , 而剩下的节点是到 \(v\)

现在把式子列出来：

设集合 \(S\) 包含以 \(mid\) 为子树的的节点（黄色方框包含的节点），集合 \(T\) 包含剩下的节点（绿色方框包含的节点）

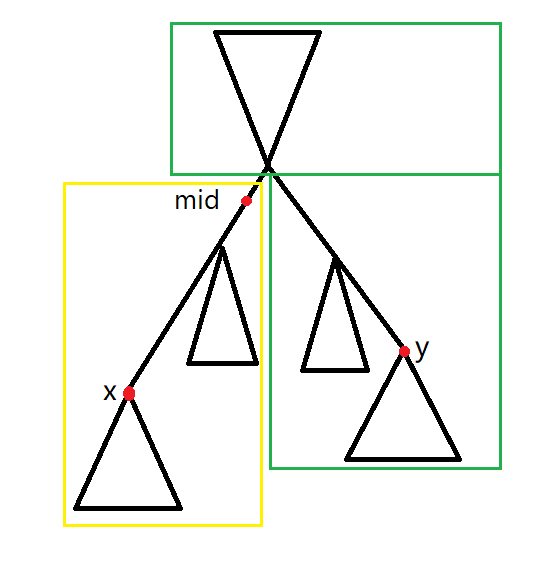
\(ans=\sum\limits_{u \in S} dist(u,x)+\sum\limits_{u \in T} dist(u,y)\)

\(ans=\sum\limits_{u=1}^{n} (dist(u,x)+dist(u,y))-(\sum\limits_{u \in S} dist(u,y)+\sum\limits_{u \in T} dist(u,x))\)

\(ans=\sum\limits_{u=1}^{n} (dist(u,x)+dist(u,y))-(\sum\limits_{u \in S} dist(u,mid)+\sum\limits_{u \in T} dist(u,mid)+sz_{mid} \times dist(mid,y)+(n-sz_{mid}) \times dist(mid,x))\)

\(ans=\sum\limits_{u=1}^{n} (dist(u,x)+dist(u,y)-dist(u,mid))-sz_{mid} \times dist(mid,y)-(n-sz_{mid}) \times dist(mid,x))\)

哈哈，非常神奇的我们就可以做了

时间复杂度 \(O(n\log n)\)