[网络流24题]骑士共存问题
题目描述
在一个 n*n个方格的国际象棋棋盘上,马(骑士)可以攻击的棋盘方格如图所示。棋盘上某些方格设置了障碍,骑士不得进入
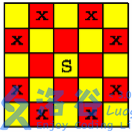
对于给定的 n*n 个方格的国际象棋棋盘和障碍标志,计算棋盘上最多可以放置多少个骑士,使得它们彼此互不攻击
题解
有个定理,大概意思是一个有向图的最小割等于该图的最大流量(说个大概,不严谨)
把每个骑士拆成入点和出点,能互相攻击的连边,求得最大流(最小割)
根据定理,断掉一些边(即在两个互相攻击的骑士只选一个)使骑士们分在两个集合里的最小代价即为最大流量
所以将总骑士数-最大流量即为答案
1 #include<queue> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 int n,m,cnt,tot; 7 int st,ed; 8 int dx[8]={1,1,-1,-1,2,2,-2,-2}; 9 int dy[8]={2,-2,2,-2,1,-1,1,-1}; 10 int head[80005]; 11 int cur[80005]; 12 int dis[80005]; 13 bool ban[205][205]; 14 struct node{ 15 int fr; 16 int to; 17 int nxt; 18 int flw; 19 }edge[1000005]; 20 void init(){ 21 memset(head,-1,sizeof(head)); 22 } 23 void addedge(int u,int v,int f){ 24 edge[cnt].fr=u; 25 edge[cnt].to=v; 26 edge[cnt].flw=f; 27 edge[cnt].nxt=head[u]; 28 head[u]=cnt++; 29 edge[cnt].fr=v; 30 edge[cnt].to=u; 31 edge[cnt].flw=0; 32 edge[cnt].nxt=head[v]; 33 head[v]=cnt++; 34 } 35 bool bfs(){ 36 queue<int>que; 37 memset(dis,0x3f,sizeof(dis)); 38 que.push(st);dis[st]=0; 39 while(!que.empty()){ 40 int u=que.front(); 41 que.pop(); 42 for(int i=head[u];i!=-1;i=edge[i].nxt){ 43 if(!edge[i].flw)continue; 44 int v=edge[i].to; 45 if(dis[v]==0x3f3f3f3f){ 46 dis[v]=dis[u]+1; 47 que.push(v); 48 } 49 } 50 } 51 return (dis[ed]!=0x3f3f3f3f); 52 } 53 int dfs(int u,int flw){ 54 int All=0;int tmp; 55 if(u==ed)return flw; 56 for(int i=head[u];i!=-1;i=edge[i].nxt){ 57 if(!edge[i].flw)continue; 58 int v=edge[i].to;head[u]=i; 59 if(dis[v]!=dis[u]+1)continue; 60 if((tmp=dfs(v,min(flw,edge[i].flw)))>0){ 61 flw-=tmp; 62 edge[i].flw-=tmp; 63 edge[i^1].flw+=tmp; 64 All+=tmp; 65 if(!flw)break; 66 } 67 } 68 return All; 69 } 70 int dicnic(){ 71 scanf("%d%d",&n,&m); 72 int ret=0;ed=n*n+1; 73 for(int i=1;i<=m;i++){ 74 int x,y; 75 scanf("%d%d",&x,&y); 76 ban[x][y]=true; 77 } 78 for(int i=1;i<=n;i++){ 79 for(int j=1;j<=n;j++){ 80 if(ban[i][j])continue; 81 for(int k=0;k<8;k++){ 82 int xx=i+dx[k]; 83 int yy=j+dy[k]; 84 if(xx<1||xx>n||yy<1||yy>n)continue; 85 if(ban[xx][yy])continue; 86 if((i+j)&1)addedge((i-1)*n+j,(xx-1)*n+yy,1); 87 else addedge((xx-1)*n+yy,(i-1)*n+j,1); 88 } 89 if((i+j)&1)addedge(st,(i-1)*n+j,1); 90 else addedge((i-1)*n+j,ed,1); 91 } 92 }memcpy(cur,head,sizeof(cur)); 93 while(bfs()){ 94 ret+=dfs(st,0x3f3f3f3f); 95 memcpy(head,cur,sizeof(head)); 96 } 97 return n*n-m-ret; 98 } 99 int main(){ 100 init(); 101 printf("%d\n",dicnic()); 102 return 0; 103 }

