优化工具-FFT/NTT

即快速傅立叶变换/快速数论变换（听着挺高端）

FFT在acm中似乎只是用于优化多项式乘法，能将一个含有n个元素的系数向量，经过O(nlogn)变成y值向量，也能经过O(nlogn)将y值向量变成系数向量（即逆FFT）。

举个例子：f(x)=ax^1+bx^2+cx^3,,,,

系数向量=（a,b,c）,y值向量=（f(x0),f(x1),f(x2)） //此处x0,x1,x2均为复数1的开根

那么他是如何体现优化的呢？

令f₂（x）=f(x)*f(x)，直接求其系数向量需要花费O(n²)。

但易知其y值向量=（f(x0)*f(x0),f(x1)*f(x1),f(x2)*(x2)），所以对f(x)做fft，在O(N)得到f₂（x）的y向量，再做逆fft，得到f₂（x）的系数向量，总复杂度O(nlogn)。

NTT即FFT的数论版，具体不懂，FFT采用的是复数运算，NTT采用的是整数运算，所以NTT精度非常好，但是NTT对于mod有条件，经典一个是，当mod=998244353时，令g=3.

对多项式的乘法的优化又体现在两个方面：

1，母函数

2，卷积定理

例题1：hdu4609

大意：从n条边中随机选出3条边，求选到的边能组成三角形的概率。（n<=100000）

枚举边c作为三角形的最大边，则有另外两条边a+b>c。

对n条边构造母函数，指数为边长，系数为对应边长的个数，则母函数的平方便是使选2条边a+b的方案数，再去除两次均选到a，先a再b和先b再a相同的情况。

对得到的母函数系数数组求前缀和，便能得到a+b>c的方案数了，但为了保证c是最大边，我们还需除掉一些情况（那些情况对边排序后就容易得到）

kuangbin的题解说得很清楚：https://www.cnblogs.com/kuangbin/archive/2013/07/24/3210565.html

  1 #include<cstdio>
  2 #include<cstdlib>
  3 #include<cstring>
  4 #include<iostream>
  5 #include<cmath>
  6 #include<algorithm>
  7 #include<map>
  8 using namespace std;
  9 typedef long long ll;
 10 const double PI = acos(-1.0);
 11 struct complex
 12 {
 13     double r,i;
 14     complex(double _r = 0,double _i = 0)
 15     {
 16         r = _r; i = _i;
 17     }
 18     complex operator +(const complex &b)
 19     {
 20         return complex(r+b.r,i+b.i);
 21     }
 22     complex operator -(const complex &b)
 23     {
 24         return complex(r-b.r,i-b.i);
 25     }
 26     complex operator *(const complex &b)
 27     {
 28         return complex(r*b.r-i*b.i,r*b.i+i*b.r);
 29     }
 30 };
 31 void change(complex y[],int len)
 32 {
 33     int i,j,k;
 34     for(i = 1, j = len/2;i < len-1;i++)
 35     {
 36         if(i < j)swap(y[i],y[j]);
 37         k = len/2;
 38         while( j >= k)
 39         {
 40             j -= k;
 41             k /= 2;
 42         }
 43         if(j < k)j += k;
 44     }
 45 }
 46 void fft(complex y[],int len,int on)
 47 {
 48     change(y,len);
 49     for(int h = 2;h <= len;h <<= 1)
 50     {
 51         complex wn(cos(-on*2*PI/h),sin(-on*2*PI/h));
 52         for(int j = 0;j < len;j += h)
 53         {
 54             complex w(1,0);
 55             for(int k = j;k < j+h/2;k++)
 56             {
 57                 complex u = y[k];
 58                 complex t = w*y[k+h/2];
 59                 y[k] = u+t;
 60                 y[k+h/2] = u-t;
 61                 w = w*wn;
 62             }
 63         }
 64     }
 65     if(on == -1)
 66         for(int i = 0;i < len;i++)
 67             y[i].r /= len;
 68 }
 69 ll num[200005],sum[200005];
 70 complex x1[400005];
 71 int a[100005];
 72 int main()
 73 {
 74     int t;
 75     cin>>t;
 76     while(t--)
 77     {    memset(num,0,sizeof num);
 78         int n;
 79         scanf("%d",&n);
 80         int mx=0;
 81         for(int i=1;i<=n;i++)
 82         {
 83             scanf("%d",&a[i]);
 84             num[a[i]]++;
 85             mx=max(a[i],mx);
 86         }
 87         int len=1,len1=mx+1;
 88         while( len < 2*len1 )len <<= 1;
 89         for(int i=0;i<len1;i++)
 90             x1[i]=complex(num[i],0);
 91         for(int i=len1;i<len;i++)
 92             x1[i]=complex(0,0);
 93         fft(x1,len,1);
 94         for(int i=0;i<len;i++)
 95             x1[i]=x1[i]*x1[i];
 96         
 97         fft(x1,len,-1);    
 98         for(int i=0;i<2*len1;i++)
 99             num[i]=(ll)(x1[i].r+0.5);
100         for(int i=1;i<=n;i++)
101             num[2*a[i]]--;
102         for(int i=1;i<=2*mx;i++)
103             num[i]/=2;
104     
105         sum[0]=0;
106         for(int i=1;i<=2*mx;i++)
107             sum[i]=sum[i-1]+num[i];
108         ll cnt=0;
109         for(int i=1;i<=n;i++)
110         {
111             cnt+=sum[2*mx]-sum[a[i]];
112             cnt-=(ll)(i-1)*(n-i);
113             cnt-=(ll)(n-i)*(n-i-1)/2;
114             cnt-=n-1;    
115         }
116         ll tot=(ll)n*(n-1)*(n-2)/6;
117         printf("%.7f\n",(double)cnt/tot);
118         
119     }
120     
121     return 0;
122 }

View Code1

例题2：Prime Distance On Tree

大意：在一棵n个节点的树上随机选两个节点，求两个节点的距离为素数的概率（n<=50000）

结合点分治后就和上面题的分析差不多了，预处理出节点的深度后，即先选经过根的左端点，再选经过根的右端点，之后再考虑去除不合理情况，O(nlognlogn)。

  1 #include <cstdio>
  2 #include <cstring>
  3 #include <algorithm>
  4 #include<cmath>
  5 #include<iostream>
  6 #define N 50010
  7 using namespace std;
  8 int m , head[N] , to[N << 1] , len[N << 1] , next2[N << 1] , cnt , si[N] , deep[N] ;
  9 int root , vis[N] , f[N] , sn , d[N] , tot ;
 10 long long ans;
 11 bool g[100005];
 12 int p[10000];
 13 void add(int x , int y , int z)
 14 {
 15     to[++cnt] = y , len[cnt] = z , next2[cnt] = head[x] , head[x] = cnt;
 16 }
 17 void getroot(int x , int fa)
 18 {
 19     f[x] = 0 , si[x] = 1;
 20     int i;
 21     for(i = head[x] ; i ; i = next2[i])
 22         if(to[i] != fa && !vis[to[i]])
 23             getroot(to[i] , x) , si[x] += si[to[i]] , f[x] = max(f[x] , si[to[i]]);
 24     f[x] = max(f[x] , sn - si[x]);
 25     if(f[root] > f[x]) root = x;
 26 }
 27 void getdeep(int x , int fa)
 28 {
 29     d[++tot] = deep[x];
 30     int i;
 31     for(i = head[x] ; i ; i = next2[i])
 32         if(to[i] != fa && !vis[to[i]])
 33             deep[to[i]] = deep[x] + len[i] , getdeep(to[i] , x);
 34 }
 35 const double PI = acos(-1.0);
 36 struct complex
 37 {
 38     double r,i;
 39     complex(double _r = 0,double _i = 0)
 40     {
 41         r = _r; i = _i;
 42     }
 43     complex operator +(const complex &b)
 44     {
 45         return complex(r+b.r,i+b.i);
 46     }
 47     complex operator -(const complex &b)
 48     {
 49         return complex(r-b.r,i-b.i);
 50     }
 51     complex operator *(const complex &b)
 52     {
 53         return complex(r*b.r-i*b.i,r*b.i+i*b.r);
 54     }
 55 };
 56 void change(complex y[],int len)
 57 {
 58     int i,j,k;
 59     for(i = 1, j = len/2;i < len-1;i++)
 60     {
 61         if(i < j)swap(y[i],y[j]);
 62         k = len/2;
 63         while( j >= k)
 64         {
 65             j -= k;
 66             k /= 2;
 67         }
 68         if(j < k)j += k;
 69     }
 70 }
 71 void fft(complex y[],int len,int on)
 72 {
 73     change(y,len);
 74     for(int h = 2;h <= len;h <<= 1)
 75     {
 76         complex wn(cos(-on*2*PI/h),sin(-on*2*PI/h));
 77         for(int j = 0;j < len;j += h)
 78         {
 79             complex w(1,0);
 80             for(int k = j;k < j+h/2;k++)
 81             {
 82                 complex u = y[k];
 83                 complex t = w*y[k+h/2];
 84                 y[k] = u+t;
 85                 y[k+h/2] = u-t;
 86                 w = w*wn;
 87             }
 88         }
 89     }
 90     if(on == -1)
 91         for(int i = 0;i < len;i++)
 92             y[i].r /= len;
 93 }
 94 
 95 
 96 complex x1[N*4];
 97 
 98 long long num[N*2];
 99 
100 
101 long long calc(int x)
102 {
103     tot = 0 , getdeep(x , 0);
104     long long sum=0,mx=0;
105     memset(num,0,sizeof num);
106     for(int i=1;i<=tot;i++)
107     {
108         num[d[i]]++;
109     
110         mx=max(mx,(long long)d[i]);
111     }
112    
113     int len1=mx+1,len=1;
114     while(len<2*len1) len*=2;
115     for(int i=0;i<len1;i++) x1[i]=complex(num[i],0);
116     for(int i=len1;i<len;i++) x1[i]=complex(0,0);
117     fft(x1,len,1);
118     for(int i=0;i<len;i++)
119         x1[i]=x1[i]*x1[i];
120        fft(x1,len,-1);
121        for(int i=0;i<=2*mx;i++)
122            num[i]=(long long)(x1[i].r+0.5);
123     for(int i=1;i<=tot;i++) num[2*d[i]]--;
124     for(int i=0;i<=2*mx;i++) num[i]/=2;
125 
126     for(int i=1;p[i]<=2*mx;i++)
127     {
128         sum+=num[p[i]];
129         
130     }  
131     
132     return sum;
133 }
134 void dfs(int x) 
135 {
136     deep[x] = 0 , vis[x] = 1 , ans += calc(x);
137     int i;
138     for(i = head[x] ; i ; i = next2[i])
139         if(!vis[to[i]])
140             deep[to[i]] = len[i] , ans -= calc(to[i]) , sn = si[to[i]] , root = 0 , getroot(to[i] , 0) , dfs(root);
141 }
142 int main()
143 {    
144     int n , i , x , y , z,tot=0;
145     for(int i=2;i<=100000;++i)
146     {
147         if(g[i]==0)
148             p[++tot]=i;
149         for(int j=1;j<=tot&&p[j]*i<=100000;++j)
150         {
151             g[i*p[j]]=1;
152             if(i%p[j]==0)
153                 break;
154         }
155     }
156 
157     while(~scanf("%d" , &n))
158     {
159         memset(head , 0 , sizeof(head));
160         memset(vis , 0 , sizeof(vis));
161         cnt = 0 , ans = 0;
162         for(i = 1 ; i < n ; i ++ )
163             scanf("%d%d" , &x , &y) , add(x , y , 1) , add(y , x , 1);
164         f[0] = 0x7fffffff , sn = n;
165         root = 0 , getroot(1 , 0) , dfs(root);
166         long long ss=(long long)n*(n-1)/2;
167          printf("%.6f\n" , (double)ans/ss);
168     }
169     return 0;
170 }

View Code2

例题3：He is Flying

大意：有n个数(n<=100000)，求区间和为s的所有区间的长度和。

其实确定一个区间也可以看成先选左端点，后选右端点。题解构造的母函数：

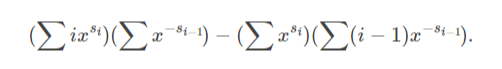
S_i为前缀和，容易发现乘起来后指数就是区间和，两式相减后系数即为区间长度，，构造的真是妙啊，，这样就成了fft裸题了。

注意指数为负数的情况，可以整体加一个偏移量，注意构造系数向量时要用+=（我就在这里卡了好久）

  1 #include <stdio.h>
  2 #include <iostream>
  3 #include <string.h>
  4 #include <algorithm>
  5 #include <math.h>
  6 using namespace std;
  7 typedef long long ll;
  8 typedef long double ld;
  9 const ld PI = acos(-1.0);
 10 struct complex
 11 {
 12     ld r,i;
 13     complex(ld _r = 0,ld _i = 0)
 14     {
 15         r = _r; i = _i;
 16     }
 17     complex operator +(const complex &b)
 18     {
 19         return complex(r+b.r,i+b.i);
 20     }
 21     complex operator -(const complex &b)
 22     {
 23         return complex(r-b.r,i-b.i);
 24     }
 25     complex operator *(const complex &b)
 26     {
 27         return complex(r*b.r-i*b.i,r*b.i+i*b.r);
 28     }
 29 };
 30 void change(complex y[],int len)
 31 {
 32     int i,j,k;
 33     for(i = 1, j = len/2;i < len-1;i++)
 34     {
 35         if(i < j)swap(y[i],y[j]);
 36         k = len/2;
 37         while( j >= k)
 38         {
 39             j -= k;
 40             k /= 2;
 41         }
 42         if(j < k)j += k;
 43     }
 44 }
 45 void fft(complex y[],int len,int on)
 46 {
 47     change(y,len);
 48     for(int h = 2;h <= len;h <<= 1)
 49     {
 50         complex wn(cos(-on*2*PI/h),sin(-on*2*PI/h));
 51         for(int j = 0;j < len;j += h)
 52         {
 53             complex w(1,0);
 54             for(int k = j;k < j+h/2;k++)
 55             {
 56                 complex u = y[k];
 57                 complex t = w*y[k+h/2];
 58                 y[k] = u+t;
 59                 y[k+h/2] = u-t;
 60                 w = w*wn;
 61             }
 62         }
 63     }
 64     if(on == -1)
 65         for(int i = 0;i < len;i++)
 66             y[i].r /= len;
 67 }
 68 
 69 complex x1[400005];
 70 complex x2[400005];
 71 complex x3[400005];
 72 ll num1[200005];
 73 
 74 ll sum[100005];
 75 int main()
 76 {
 77     int T;
 78     int n;
 79     scanf("%d",&T);
 80     while(T--)
 81     {
 82         scanf("%d",&n);
 83         int x;
 84         sum[0]=0;
 85         ll res=0,tt=0;
 86         for(int i=1;i<=n;i++)
 87         {
 88             scanf("%d",&x);
 89             sum[i]=x+sum[i-1];
 90             if(x==0)
 91             {
 92                 tt++;
 93                 res+=(tt+1)*tt/2;
 94             }
 95             else tt=0;
 96         }
 97         
 98         printf("%lld\n",res);
 99         int len1=2*sum[n]+1,len=1,l=0;
100         while(len<2*len1) len*=2,l++;
101         
102         
103         for(int i=0;i<len;i++)
104             x1[i]=complex(0,0);
105            for(int i=0;i<len;i++)
106             x2[i]=complex(0,0);
107         for(int i=1;i<=n;i++)
108         {
109         x1[sum[i]+sum[n]].r+=i;
110 
111         }
112      
113         for(int i=1;i<=n;i++)
114         {
115         x2[-sum[i-1]+sum[n]].r+=1;
116 
117         }
118     
119         fft(x1,len,1);
120         fft(x2,len,1);
121         for(int i=0;i<len;i++)
122             x1[i]=x1[i]*x2[i];
123            fft(x1,len,-1);
124        
125         for(int i=0;i<len;i++)
126             x3[i]=complex(0,0);
127            for(int i=0;i<len;i++)
128             x2[i]=complex(0,0);
129         for(int i=1;i<=n;i++)
130         x3[sum[i]+sum[n]].r+=1;
131         for(int i=1;i<=n;i++)
132         x2[-sum[i-1]+sum[n]].r+=i-1;
133          fft(x3,len,1);
134         fft(x2,len,1);
135         for(int i=0;i<len;i++)
136             x3[i]=x3[i]*x2[i];
137            fft(x3,len,-1);
138            for(int i=1+2*sum[n];i<=3*sum[n];i++)
139            {    
140             printf("%lld\n",(ll)(x1[i].r-x3[i].r+0.5));
141            }
142         
143         
144     
145         
146     }
147     return 0;
148 }