倍增算法1

首先用倍增法解决一道求区间最大值问题，算是倍增的入门了。

其实也算是一种dp，不过大家把这个二维dp数组叫做ST表。

ST表数组：f[i][j]，表示区间【i，i+2^j-1】的最大值。这个区间的大小是2^j个数。

ST表的初始化：f[i][0]=a[i]。（显然这是区间大小为1的时候）

ST表的递推过程：

1，由区间大小为1的项转移得到区间大小为2¹的项

2，由区间为2¹的项转移得到区间为2²的项

3，由区间为2²的项转移得到区间为2³的项

。。。

这就是倍增的由来了吧。

这个递推过程的代码：

void RMQ(int N){
    for(int j=1;(1<<j)<=N;j++)    
    for(int i=1;i<=N;i++)
        if(i+(1<<j)-1<=N)
         f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]); 
}

 

经过处理后，访问一段长区间便能利用事先处理好的数据得出答案

比如询问最大值的一项处理技术：

 

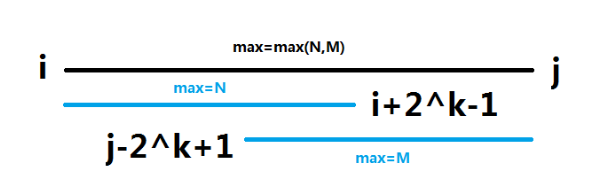
因为区间的长度为j-i+1，所以可以取k=log2(j-i+1)。

则RMQ(A,i,j)=max(f[i][k],f[j-2^k+1][k])。

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
int a[100001],f[100001][20];

void RMQ(int N){
    for(int j=1;(1<<j)<=N;j++)    
    for(int i=1;i<=N;i++)
        if(i+(1<<j)-1<=N)
         f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]); 
}
int main(){
    int N,M;
    int tt;
    cin>>tt;
    while(tt--) 
    {
        cin>>N;
    for(int i=1;i<=N;i++) cin>>a[i];
    for(int i=1;i<=N;i++) f[i][0]=a[i];
    RMQ(N); 
    cin>>M;
    while(M--){
        int l,r;
        cin>>l>>r;
         int k=(int)(log((double)(r-l+1))/log(2.0)); 
        printf("%d\n",max(f[l][k],f[r-(1<<k)+1][k]));
    }
    }
    return 0;
}