Wannafly挑战赛14 F.细胞

题解:NTT、二项式定理
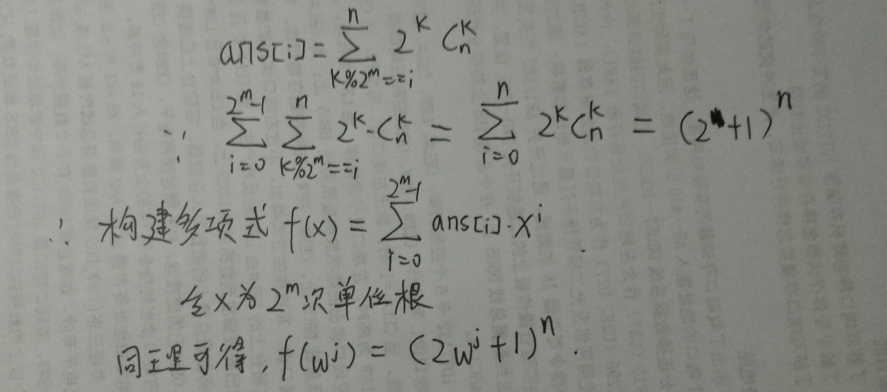
再逆FFT求出系数ans[i],本题即可解了
另:采用FFT的话,复数既不方便,误差也很大。
从FFT到NTT:
由费马小定理可知 gp-1%p=1 (p为质数)
所以利用这个性质来对应单位复数根乘方的周期性,即![]()
代码:
#include<iostream>
using namespace std;
typedef long long ll;
const ll Mod=998244353;
const ll G=3;
ll kpow(ll a,ll k)
{
ll res=1LL;
while(k>0)
{
if(k&1)res=res*a%Mod;
a=a*a%Mod;
k>>=1;
}
return res;
}
void change(ll y[],int len)
{
for(int i=1,j=len/2;i<len-1;i++)
{
if(i<j)swap(y[i],y[j]);
int k=len/2;
while(j>=k)
{
j-=k;
k/=2;
}
if(j<k)j+=k;
}
}
void fft(ll y[],int len,int on)
{
change(y,len);
for(int h=2;h<=len;h<<=1)
{
ll wn=kpow(G,(Mod-1)/h);
if(on==-1)wn=kpow(wn,Mod-2);
for(int j=0;j<len;j+=h)
{
ll w=1LL;
for(int k=j;k<j+h/2;k++)
{
ll u=y[k];
ll t=w*y[k+h/2]%Mod;
y[k]=(u+t)%Mod;
y[k+h/2]=(u-t+Mod)%Mod;
w=w*wn%Mod;
}
}
}
if(on==-1)
{
ll t=kpow(len,Mod-2);
for(int i=0;i<len;i++)
y[i]=y[i]*t%Mod;
}
}
ll a[1<<20];
int main()
{
ll n,m;
scanf("%lld%lld",&n,&m);
ll wn=kpow(G,(Mod-1)/(1<<m)),w=1;
for(int i=0;i<(1<<m);i++)
{
a[i]=kpow(2*w+1,n);
w=w*wn%Mod;
}
fft(a,(1<<m),-1);
ll res=0,buf=1;
for(int i=0;i<(1<<m);i++)
{
res=(res+a[i]*buf)%Mod;
buf=buf*2222303%Mod;
}
printf("%lld\n",res);
return 0;
}



