数论定理篇

真是的,博主本来就菜,又懒得刷题。

只好一边划水,一边从别人的博客上搬代码。
1)素数筛法
2)快速幂,快速乘
快速乘(注意:变乘法为加法):
LL Kmul(LL a, LL b, LL mo){ //计算a*b%mo
LL ret = 0;
while(b){
if(b & 1) ret = (ret + a) % mo;
a = (a+a) % mo;
b >>= 1;
}
return ret;
}
//即每次a乘2,b除2
3)欧几里得求gcd,lcm
递归,gcd(a,b)= gcd(b,a%b) = gcd(x,0) = x
lcm(a,b)= a*b/gcd(a,b) = a/gcd(a,b)*b
4)扩展欧几里得
解决ax+by=c整数解问题
5)费马-欧拉定理
I、欧拉定理
若n、a互质,a^φ(n) ≡ 1 (mod n) //同余式
II、费马小定理
若p、a互质,并且p是质数,a^(p-1) ≡1(mod p)
//循环节
6)逆元inv(解决在除法过程中取模问题)
定义:a*inv(a) ≡ 1 (mod m)
根据费马小定理,若m为质数,inv(a)=a^(m-2) //m尽量取大
若不是,转换为扩展欧几里得问题
O(n)求出2->N的逆元(MOD要为质数)
int init(){
inv[1] = 1;
for(int i = 2; i < N; i ++){
inv[i] = (MOD - MOD / i) * 1ll * inv[MOD % i] % MOD;
}
}
7)欧拉函数φ(n)或phi(n)
phi(n)为1-n中与n互质的数的个数
模仿素数埃筛
int phi[N];
void Euler(){
phi[1] = 1;
for(int i = 2; i < N; i ++){
if(!phi[i]){
for(int j = i; j < N; j += i){
if(!phi[j]) phi[j] = j;
phi[j] = phi[j] / i * (i-1);
}
}
}
}
8)中国剩余定理
求一个x,模m1余r1,模m2余r2,......
若m1,m2....两两互质,则x有解。
模板代码:

1 #include<cstdio>
2 #include<algorithm>
3 using namespace std;
4 typedef long long LL;
5 typedef pair<LL, LL> PLL;
6 LL a[100000], b[100000], m[100000];
7 LL gcd(LL a, LL b){
8 return b ? gcd(b, a%b) : a;
9 }
10 void ex_gcd(LL a, LL b, LL &x, LL &y, LL &d){
11 if (!b) {d = a, x = 1, y = 0;}
12 else{
13 ex_gcd(b, a % b, y, x, d);
14 y -= x * (a / b);
15 }
16 }
17 LL inv(LL t, LL p){
18 LL d, x, y;
19 ex_gcd(t, p, x, y, d);
20 return d == 1 ? (x % p + p) % p : -1;
21 }
22 PLL linear(LL A[], LL B[], LL M[], int n) {
23 LL x = 0, m = 1;
24 for(int i = 0; i < n; i ++) {
25 LL a = A[i] * m, b = B[i] - A[i]*x, d = gcd(M[i], a);
26 if(b % d != 0) return PLL(0, -1);
27 LL t = b/d * inv(a/d, M[i]/d)%(M[i]/d);
28 x = x + m*t;
29 m *= M[i]/d;
30 }
31 x = (x % m + m ) % m;
32 return PLL(x, m);
33 }
34 int main(){
35 int n;
36 while(scanf("%d", &n) != EOF){
37 for(int i = 0; i < n; i ++){
38 a[i] = 1;
39 scanf("%d%d", &m[i], &b[i]); //分别为m,r
40 }
41 PLL ans = linear(a, b, m, n);
42 if(ans.second == -1) printf("-1\n");
43 else printf("%lld\n", ans.first);
44 }
45 }
9)大组合数,卢卡斯定理(p为质数)
C(n, m) % p = C(n / p, m / p) * C(n%p, m%p) % p //递归
10)说到组合,斯特林数,卡特兰数 //数列工具OEIS
第二类斯特林数:将有n个元素的集合划分成m个集合(没有空集合),有多少种划分,递推式:
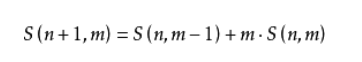
另斯特林公式近似求n!:
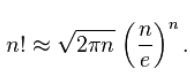
求n!的位数: // (int)lg(n!) + 1
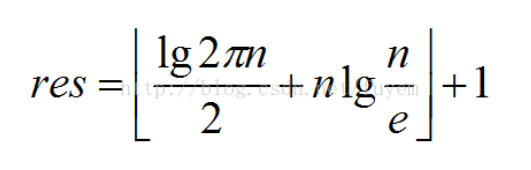
卡特兰数://出栈序列
其前几项为 : 1, 1, 2, 5, 14, 42, 132, 429,
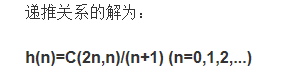
若n次入栈,m次出栈:C(n+m,n)-C(n+m,m-1)



