20230201 模拟赛改题
T1 课后练习题
简要题意:求方程 \(x^k\equiv n\ (\bmod\ x + 1)\) 的解的个数,\(1\le n,k\le 10^{14}\)。
可以尝试找规律:
当 \(k=1\) 时:
答案就是 \(n+1\) 的约数个数 \(-1\)。
当 \(k=2\) 时:
剩下的与 \(k=1\) 时的做法类似,只不过答案变成了 \(n-1\) 的约数个数 \(-1\)。
当 \(k=3\) 时:
剩下的与 \(k=2\) 时的做法类似,只不过答案变成了 \(n+1\) 的约数个数 \(-1\)。
总结出规律:当 \(k\) 为奇数时,答案是 \(n+1\) 的约数个数 \(-1\),否则答案是 \(n-1\) 的约数个数 \(-1\)。
code:
#include<iostream>
using namespace std;
int main() {
long long n, k, ans = 0;
scanf("%lld%lld", &n, &k);
if(k & 1) n++;
else n--;
for(long long i = 1; i * i <= n; i++) {
if(n % i == 0) {
if(n / i == i) ans++;
else ans += 2;
}
}
printf("%lld", ans - 1);
return 0;
}
T2 拼图
求用无数个 \(2\times 2\) 和 \(1\times 4\) 的拼图拼出一块 \(4\times n\) 的拼图的方案数,\(n\le 10^{18}\)。
首先公布结论:\(dp_i=dp_{i-1}+dp_{i-2}+5\times dp_{i-4}-dp_{i-5}+dp_{i-6}-dp_{i-8}\)。
接下来我来证明这个式子:
考虑上一个位置的拼图的情况,无非就 \(3\) 种,列举在下图:
Case 1:

情况 a 最简单,方案数就是 \(dp_{i-1}\)。
接下来考虑 Case 1 的情况 b:
无非也是 \(3\) 种情况,列举在下图:
Case 2:
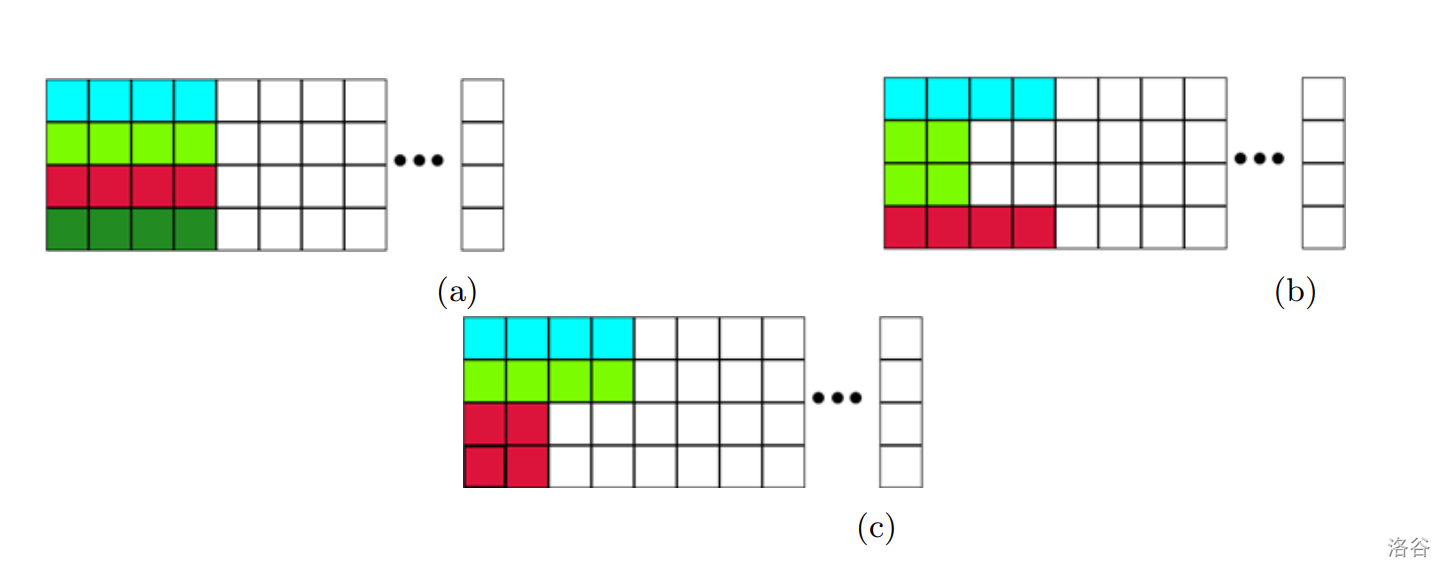
那么我们考虑 Case 2 的情况 a:答案就是 \(dp_{i-4}\)。
接下来考虑情况 b:
我们令 \(x_i\) 表示这种情况中从 \(1\) 到第 \(i\) 个位置对总答案的贡献,这次只有两种情况,列举在下图:
Case 3:

考虑 Case 3 的情况 a:答案就是 \(dp_{i-4}\)。
考虑 Case 3 的情况 b,这种情况的答案就是 \(x_{i-4}\)。
所以 \(x_i=dp_{i-4}+x_{i-4}\)。
接下来考虑 Case 2 中的情况 c,我们令 \(y_i\) 表示这种情况中从 \(1\) 到第 \(i\) 个位置对总答案的贡献,此时有 \(2\) 种情况:
Case 4:

考虑 Case 4 中的情况 a,显然,答案为 \(dp_{i-4}\)。
接下来考虑 Case 4 中的情况 b,此时答案为 \(y_{i-2}\)。
所以 \(y_i=dp_{i-4}+y_{i-2}\)。
此时 Case 1 中情况 b 的答案就是:
接下来考虑 Case 1 中的情况 c,我们令 \(z_i\) 表示这种情况中从 \(1\) 到第 \(i\) 个位置对总答案的贡献,此时有 \(2\) 种情况:
Case 5:

对于 Case 5 中的情况 a,答案为 \(dp_{i-2}\)。
对于 Case 5 中的情况 b,此时答案为 \(z_{i-2}\)。
所以 \(z_{i}=dp_{i-2}+z_{i-2}\)。
所以 Case 1 中的情况 c 的答案就是:
所以总答案就是:
这时我们令 \(i=i-4\) 再求一遍 \(dp_{i}\):
所以:
回到 \(dp_i\) 的式子:
证毕。
当然,只是这一个式子很明显会超时,我们还需要一些优化。
考虑用矩阵乘法优化这个过程:
首先构造初始矩阵:
我们的目标是转移到这个矩阵:
根据上面的递推关系,我们很容易构造出中间矩阵:
直接上矩阵快速幂就好了 qwq:
#include<iostream>
#include<cstring>
using namespace std;
const long long mod = 1e9 + 7;
const long long res[] = {1, 1, 2, 3, 9, 16, 35, 65, 143};
struct Matrix {
int n, m;
long long a[10][10];
Matrix() {memset(a, 0, sizeof(a));}
Matrix operator * (const Matrix& x) const {
Matrix res;
res.n = n, res.m = x.m;
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= x.m; j++) {
for(int k = 1; k <= m; k++) {
res.a[i][j] = (res.a[i][j] + a[i][k] * x.a[k][j]) % mod;
}
}
}
return res;
}
} a, BASE;
void init() {
a.n = 1, a.m = 8;
for(int i = 1; i <= 8; i++) {
a.a[1][i] = res[i];
}
BASE.n = BASE.m = 8;
BASE.a[1][8] = -1, BASE.a[2][1] = 1;
BASE.a[3][2] = 1, BASE.a[4][3] = 1;
BASE.a[3][8] = 1, BASE.a[4][8] = -1;
BASE.a[5][4] = 1, BASE.a[5][8] = 5;
BASE.a[6][5] = 1, BASE.a[7][6] = 1;
BASE.a[7][8] = 1, BASE.a[8][7] = 1;
BASE.a[8][8] = 1;
}
Matrix fpow(long long b) {
Matrix ans = a;
while(b) {
if(b & 1) ans = ans * BASE;
BASE = BASE * BASE;
b >>= 1;
}
return ans;
}
int main() {
long long n;
scanf("%lld", &n);
if(n <= 8) return printf("%lld", res[n]) & 0;
init();
printf("%lld", fpow(n - 8).a[1][8]);
return 0;
}

