机器学习 - 课程笔记
线性回归
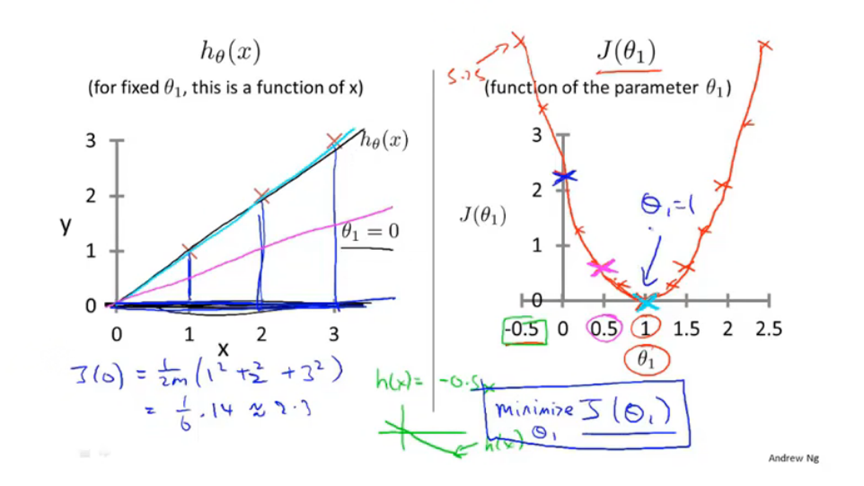
代价函数J,也被称为平方误差函数,用来描述假设函数值与真实值的误差大小。其中乘1/2是用于减少平均误差,并且后面求导会有一个2,可以消掉。线性回归的代价函数常用平方误差函数。


假设函数的参数是x,代价函数的参数是θ。
梯度下降法
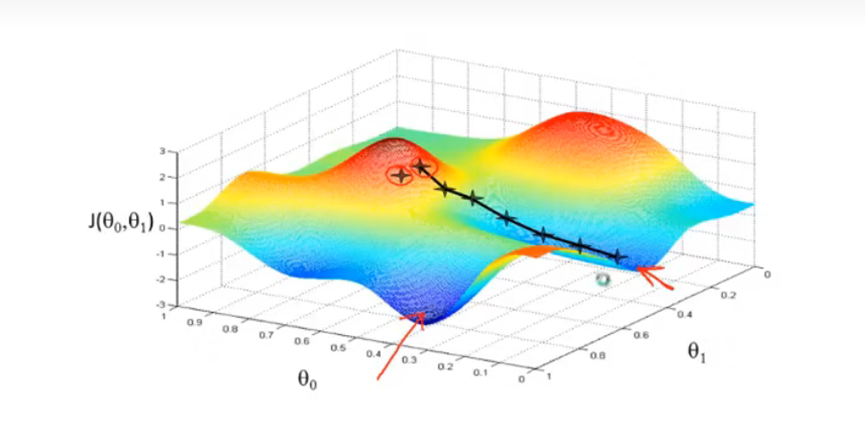
要得到最小化代价函数的Θ0和Θ1参数,在代价函数中将Θ0和Θ1初始化为0,然后不断改变Θ0和Θ1来减小代价函数的值。

选择不同的初始点会得到不同的结果
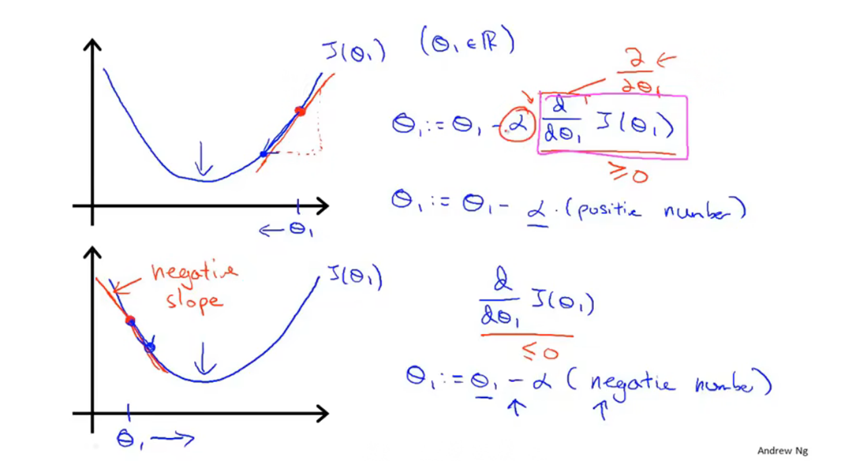
梯度下降法公式,
α是学习速率,用来控制下降的步长大小。如果设置太小会使得变化太慢,如果设置太大会使得步长太大而可能无法达到最低点。
后面的是导数项,即代价函数对Θj的偏导。如果保持α不变,下降的步长也会越来越小,因为导数项(切线斜率)会越来越小。
需要注意的是应该用左边的写法进行赋值,保证Θ0和Θ1同时变化。右边的写法是错误的,这是另一种算法。
多元情况下,同样对每个维度进行下降,然后同时变化。·

梯度下降法可能无法找到全局最优点,如果初始点在局部最优点,则不会变化。
线性回归的代价函数是一个碗状的函数,术语叫做凸函数。它只有一个全局最优点,适合用梯度下降法。
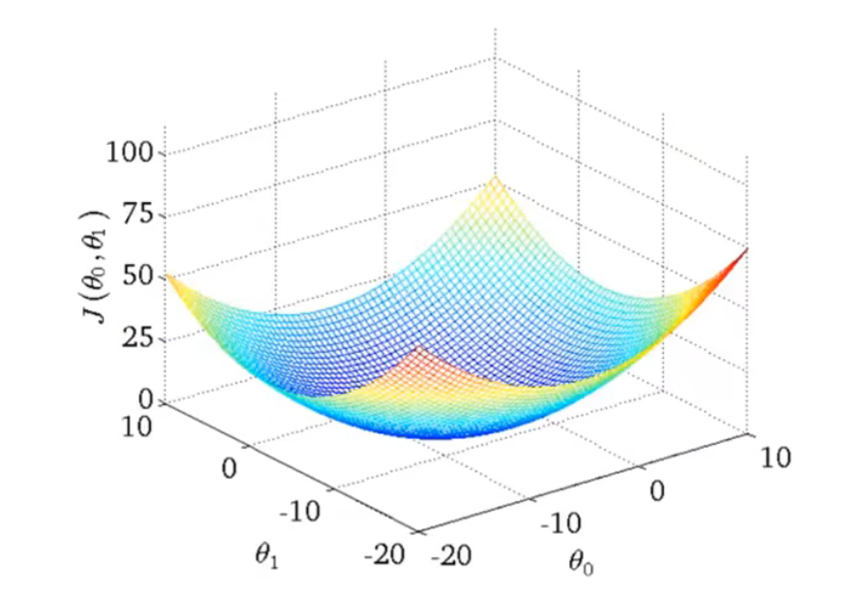
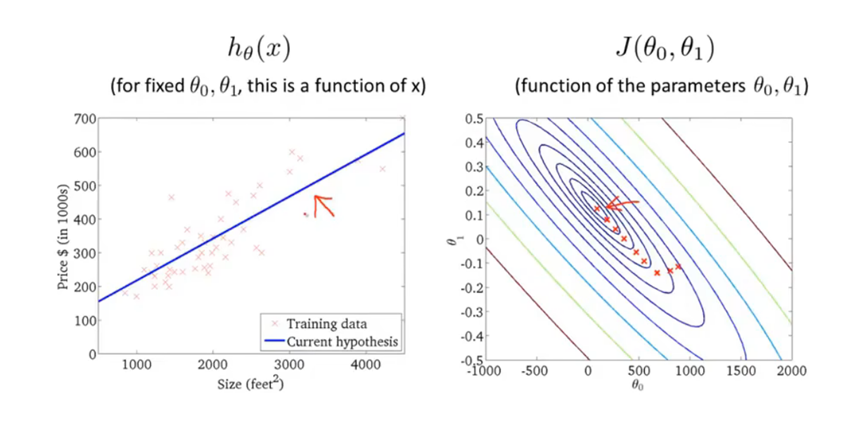
将梯度下降法用于线性回归模型。
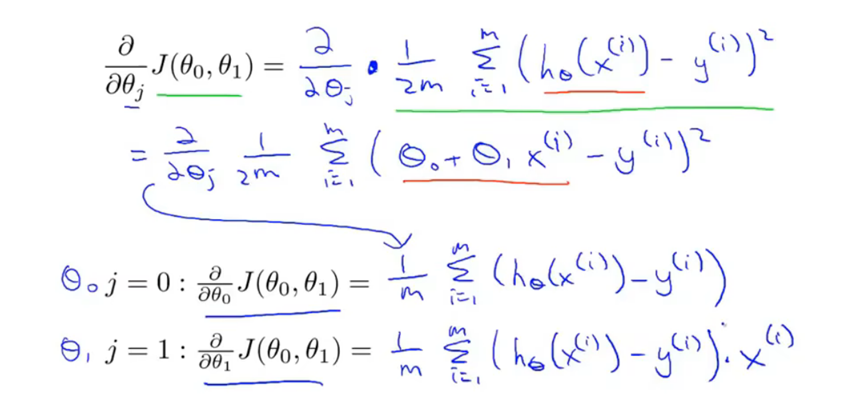
多元梯度下降法
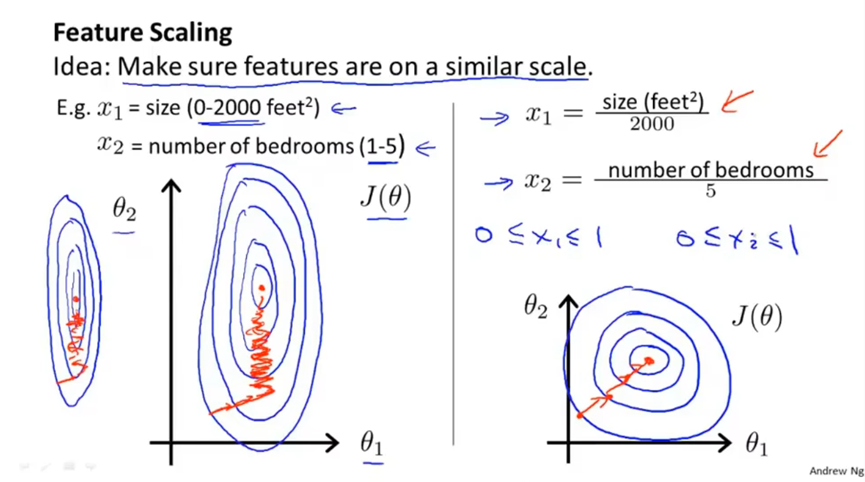
多元梯度下降法------特征缩放,将所有特征缩放到相近的尺度,如缩放到0-1内。但是尺度太大或太小也不好,比如大于[-3,3]和小于[-1/3,1/3]。另外特征缩放只是为了让梯度下降运行的更快一点,尺度也不要求特别精确。
下面中原来的两个特征值尺度相差过大,在梯度下降时会很慢,这里直接除以最大值,缩放到[0,1]内。
均值归一化,将xi替换为xi-μi,让特征值具有为0的平均值。其中μi是训练集中特征xi的均值。然后除以该特征值的范围si,这里范围si指最大值减去最小值。

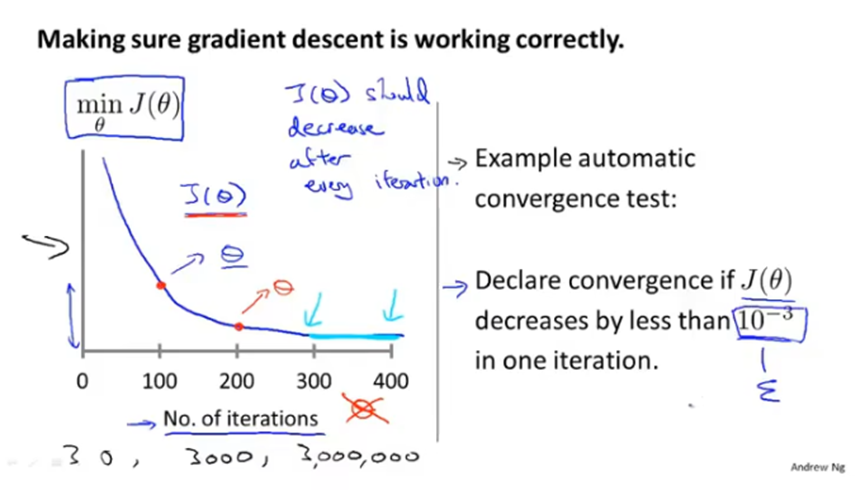
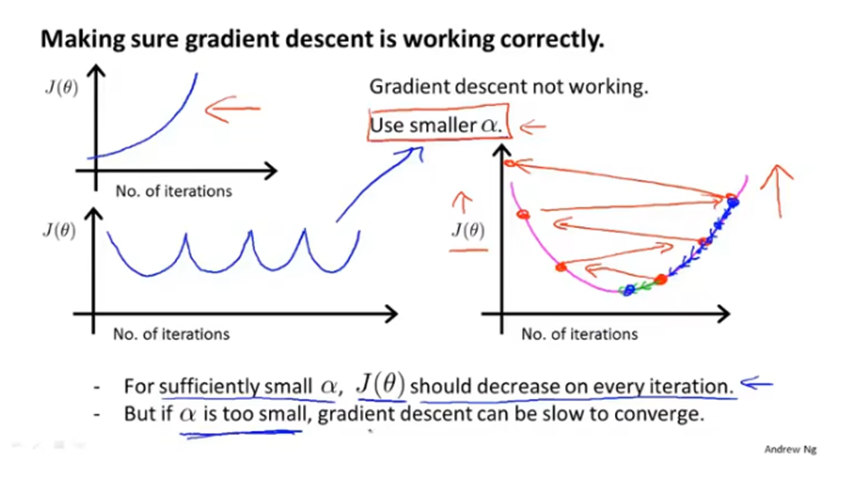
代价函数随着梯度下降迭代次数变化的曲线图,正常来说代价函数的值应该是逐渐减少的,并且从图中可以看出是否已经收敛。
如果曲线图中代价函数的值是升高的,说明学习率α可能设置过大了,应该减小学习率α。如果曲线一会升高一会又降低,也应该减小学习率α。
一般可以选择以3为倍数进行调试,如..., 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1,...
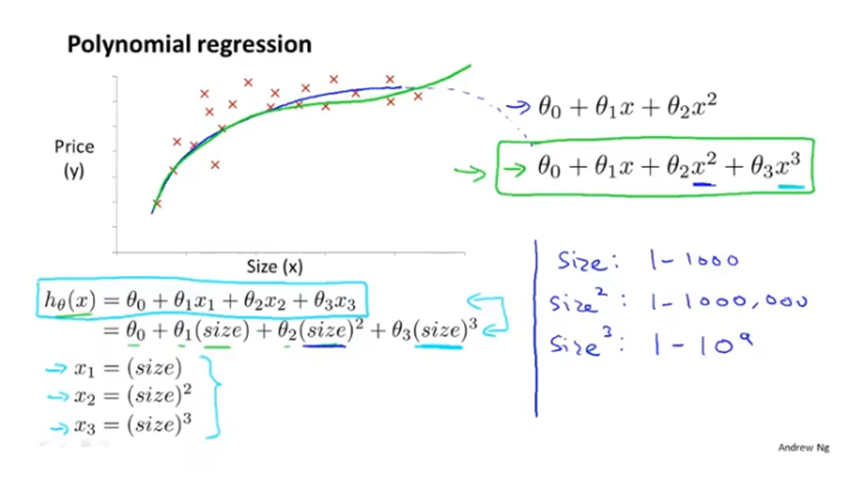
多项式回归
多项式回归,将多次项作为一个新的变量,这样就能继续应用线性回归的方法。注意这时使用特征缩放就更重要了。
正规方程
正规方程,区别于使用迭代方法的梯度下降,是通过数学计算直接得到最小化代价函数的θ值。
具体为,对代价函数J(θ)的每个特征变量求偏导数,然后将它们全部置零,计算出对应的θ1,
θ2,..., θn,从而得到最小化代价函数J的θ值。
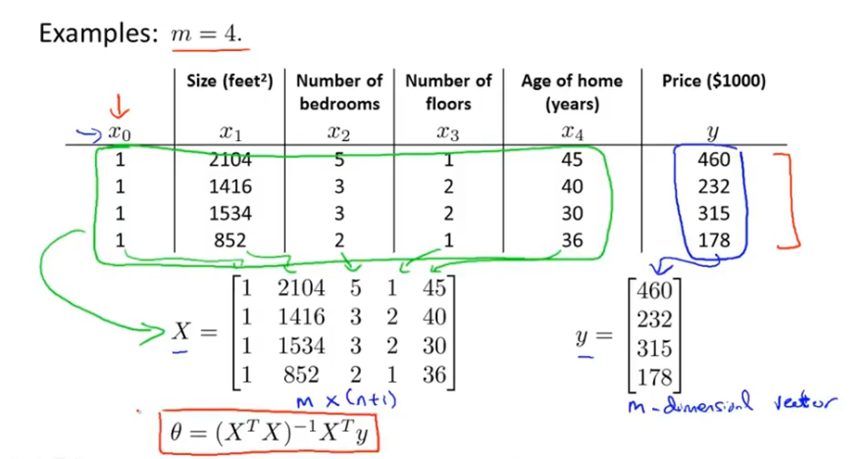
使用正规方程法仅需要进行如下步骤:对数据集添加一个对应额外特征变量的x0;然后构建一个矩阵X,包含所有训练样本的特征变量,其中每一行是一个样本;然后将要预测的值构建一个向量y;最后按照公式计算θ即可。
使用正规方程和梯度下降的区别如下:
梯度下降需要选择学习速率α,这意味着需要运行多次来尝试不同的学习速率α;梯度下降需要进行多次迭代,计算可能更慢。而正规方程不需要选择α,也不用迭代。
但正规方程需要计算n*n的矩阵运算,所以如果特征变量的数量n很大的话,计算会很慢,比梯度下降法会慢很多。
一般来说,如果特征数量大于一万的话,就考虑换成梯度下降法。另外正规方程没法用于逻辑回归等更复杂的算法,但在线性回归模型上,特征数量小的话,使用正规方程会更好。
逻辑回归
逻辑回归是一种分类算法,它的输出(预测值)一直在[0,1]中。
逻辑回归的假设函数是h(x)=g(θTx),如下。其中函数g(z)是sigmoid函数或称为logistic函数,g(z)永远在0到1之间。
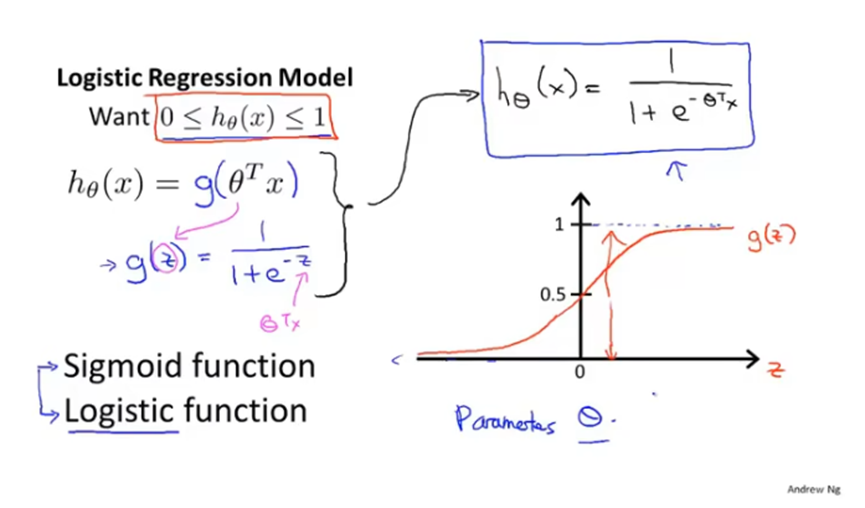
逻辑回归的假设函数表示的是在给定x和θ的条件下,y=1的概率。
当概率大于0.5时就判断y=1,当概率小于0.5时就判断y=0。而由于sigmoid函数g(z)在z=0时的函数值是0.5,所以可得到当z即θTx>0时判断y=1,当θTx<0时判断y=0。

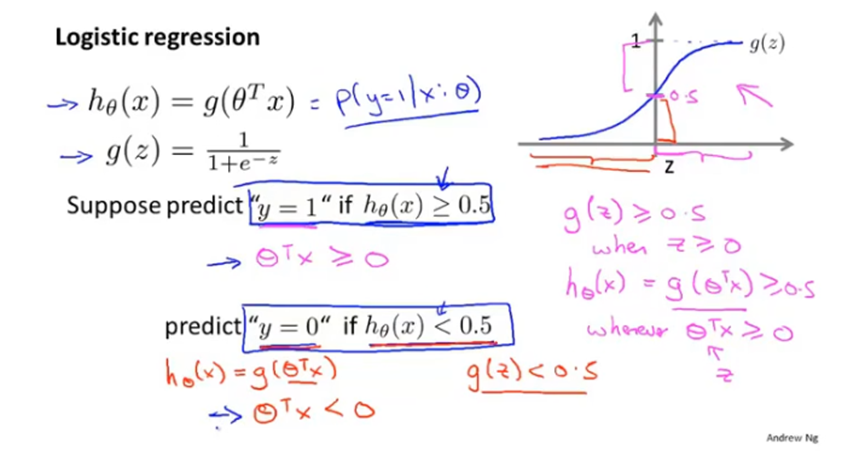
例如下图场景,θTx=-3+x1+x2,则当-3+x1+x2>=0时预测y=1。
另外对于直线-3+x1+x2=0,即x1+x2=3,整个平面被其划分,上半部分都预测y=1,下半部分都预测y=0,这条直线就被称为决策边界。
需要注意的时,决策边界是由假设函数确定的,与特征向量有关,与训练集无关。
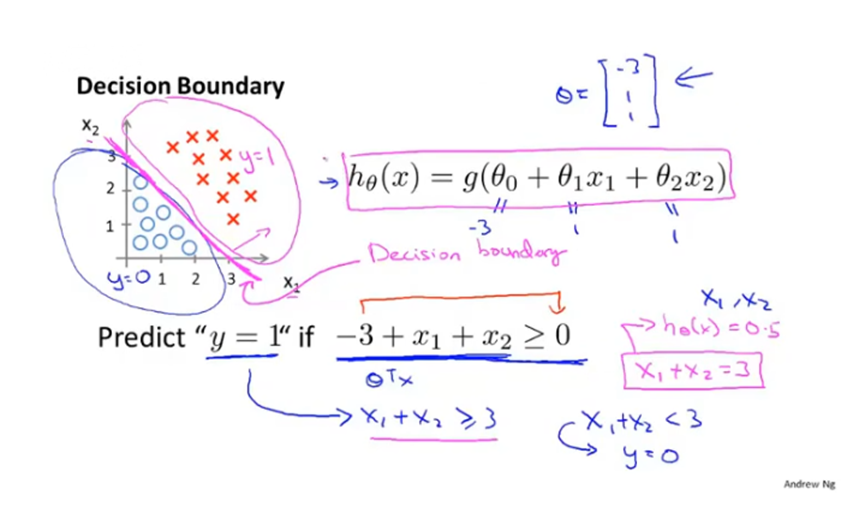
关于逻辑回归的代价函数。
首先将线性回归的平方误差代价函数写作带有cost项的形式,这个cost项就是指输出的预测值为h(x),而实际标签是y的情况下,学习算法付出的代价。
如果在逻辑回归中直接使用平方误差函数,会导致它
变成参数θ的非凸函数,有许多局部最优点,无法使用梯度下降达到全局最优点。
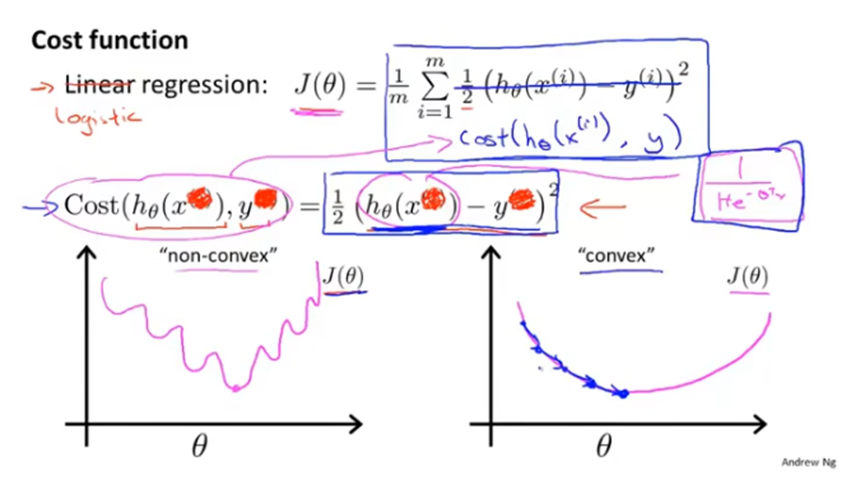
逻辑回归使用的cost项如下,根据真实标签y的值分为不同的函数。
当y=1,h(x)=1时,代价为0。
当y=1,h(x)=0时,代价为无穷大。
当y=0,h(x)=0时,代价为0。
当y=0,h(x)=1时,代价为无穷大。

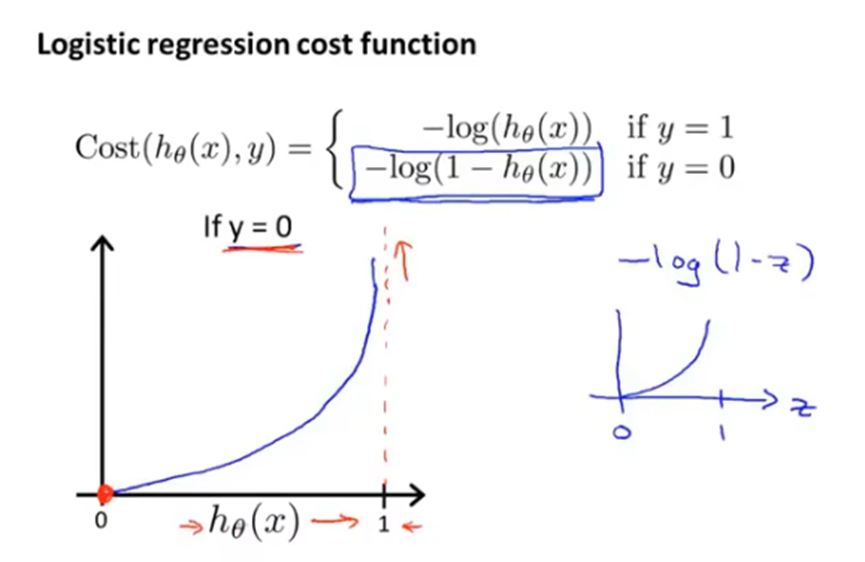
将逻辑回归代价函数的cost项用一个式子表达,得到的代价函数如下。

同样用梯度下降算法得到最小化代价函数的参数θ值。

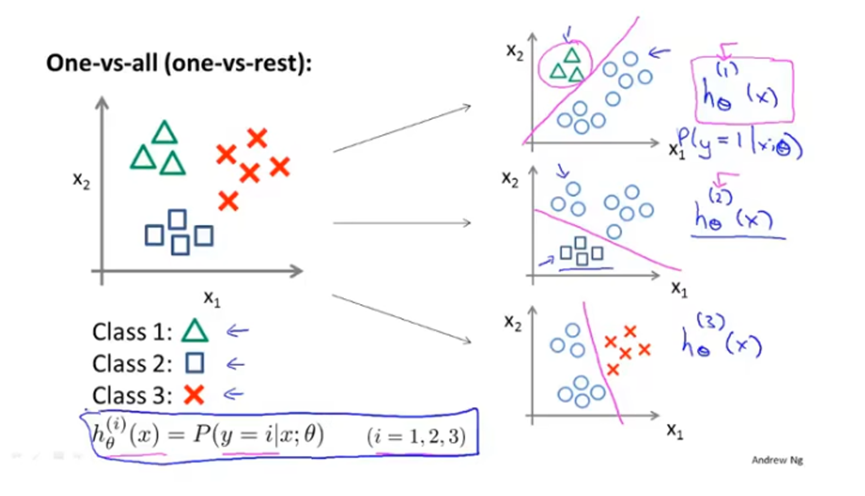
用二元分类方法解决多元分类问题
如下图所示,一个三分类问题,可以分为三个二分类问题。新建三个伪训练集,将要判断的类别(如三角)做为正类,其他类别作为负类,训练得到三个分类器。其中每个分类器的作用其实是计算出x是其正类的概率。最后从三个分类器中选择h(x)最大的预测值。
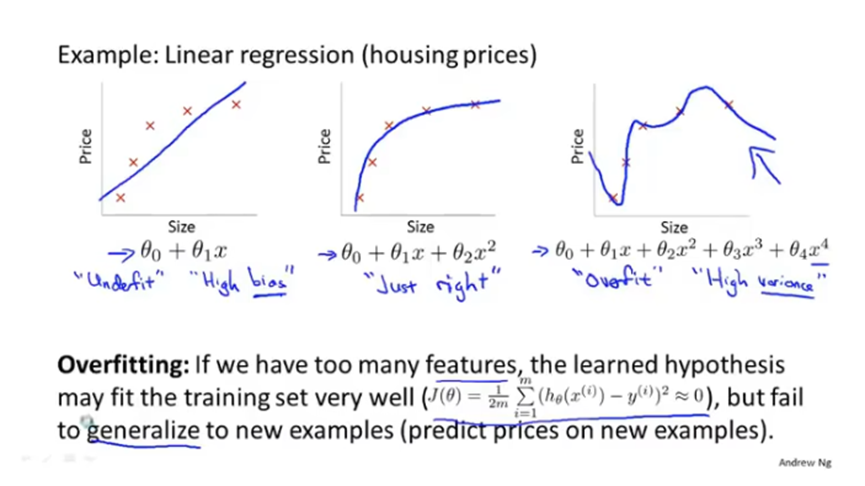
过拟合问题
假设模型过于拟合训练集,导致它无法泛化到新的样本中,无法预测新样本的值。
"泛化"是指一个假设模型应用到新样本的能力。
过拟合模型的曲线是非常扭曲的。
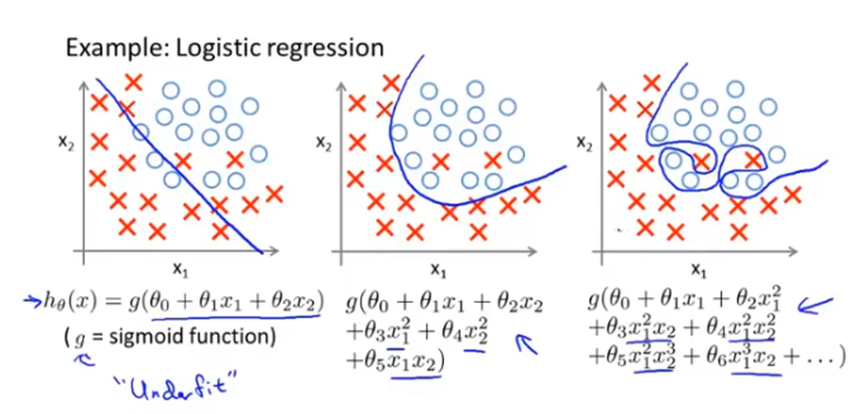
如果有过多的特征变量,但只有非常少的训练数据时,就会出现过度拟合的问题。
解决过拟合的方法:
-
尽量减少特征数量,选择更重要的特征保留。但是其舍弃了一部分特征变量,意味着也舍弃了关于问题的一些信息。
-
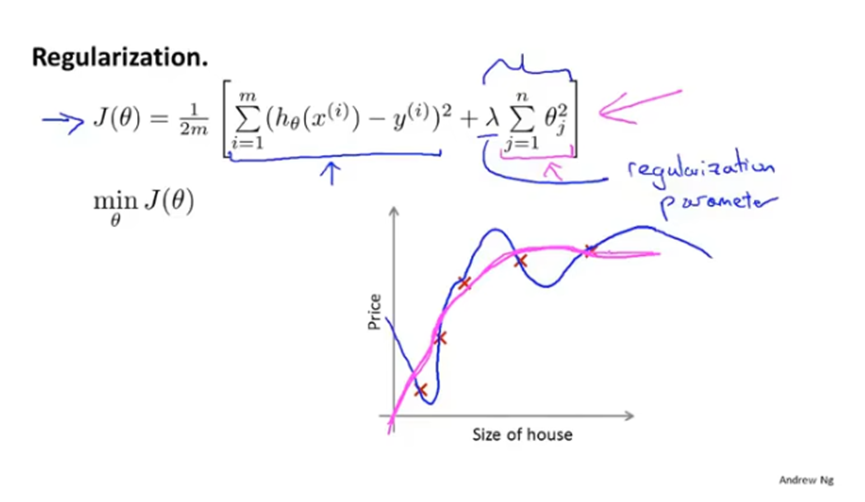
正则化,保留所有特征变量,但是减少量级或者参数θj的大小。
正则化方法如下:在代价函数后面加上正则化项(1000θ32+1000θ42),惩罚参数θ3和θ4,要让新的代价函数最小,那么θ3和θ4都要接近于0,这样一来近似于在假设函数中去掉了θ3和θ4的项。最终假设函数的曲线会近似于二次函数,只加上了一些非常小的项。
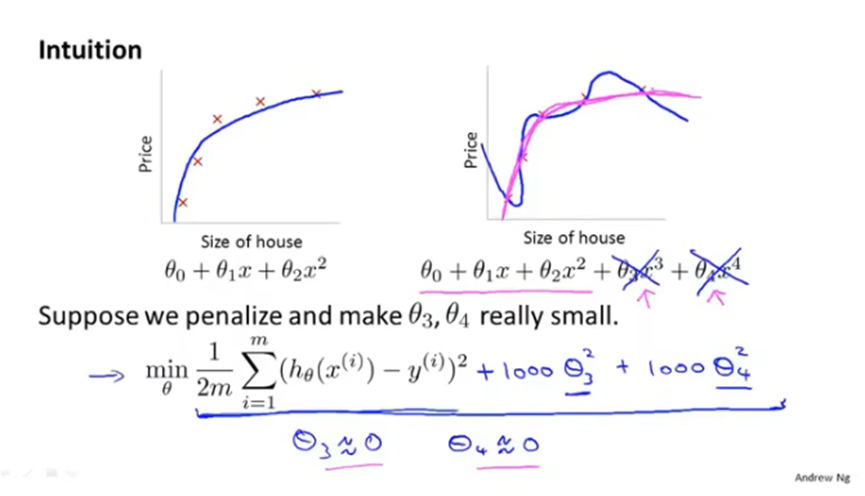
正则化的思想就是,将参数值减小,参数值较小意味着一个更简单的假设模型,曲线也越平滑,因此更不容易出现过拟合的问题。
由于我们一般不知道哪个参数的相关度更大,因此在正则化中缩小所有的参数。注意这里是从θ1到θj,不包含θ0。

最终得到的正则化代价函数如下,在一般目标的基础上加上了正则化项。其中λ是正则化参数,用于平衡两个目标(更好的拟合训练集和将参数控制的更小),加号分割的两部分即分别是这两个目标的体现。
如果正则化参数设置太大的话,会导致删掉参数项,只留下θ0,造成欠拟合。
对正则化代价函数使用梯度下降如下,即每次迭代时,对θj乘以一个比1略小的数,然后进行和之前一样的更新操作。

对正则化代价函数使用正规方程如下,加上了一个(n+1)*(n+1)的矩阵项。

逻辑回归的正则化代价函数如下,在一般目标的基础上,加上和线性回归中相同的正则化项。

对逻辑回归的正则化代价函数使用梯度下降如下,看起来和上面线性回归的相同,但其实假设函数h(x)不一样。

神经网络
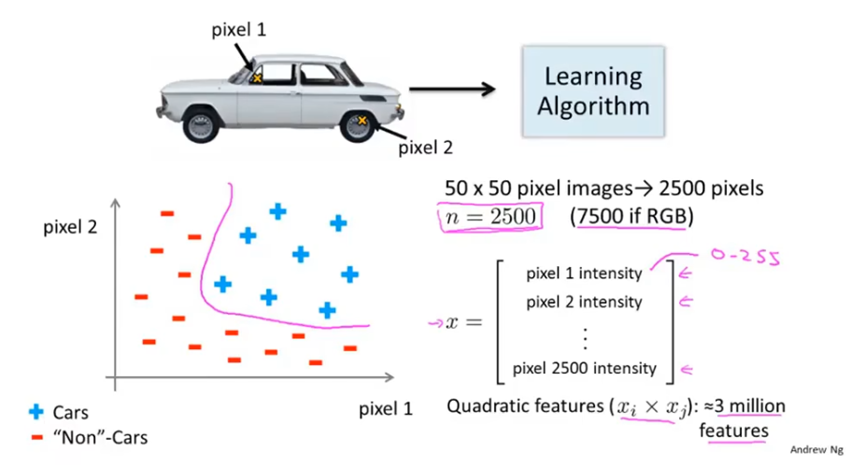
对于图像识别问题,每个像素点都作为一个特征,特征太多,维度太高。
对于只包含平方项或立方项特征的逻辑回归算法,没法处理这种特征数量太多的问题。
而神经网络是一种学习复杂的非线性假设的更好算法,即使特征数量很多也可以处理。
神经网络是模拟动物神经元或神经网络提出的算法。
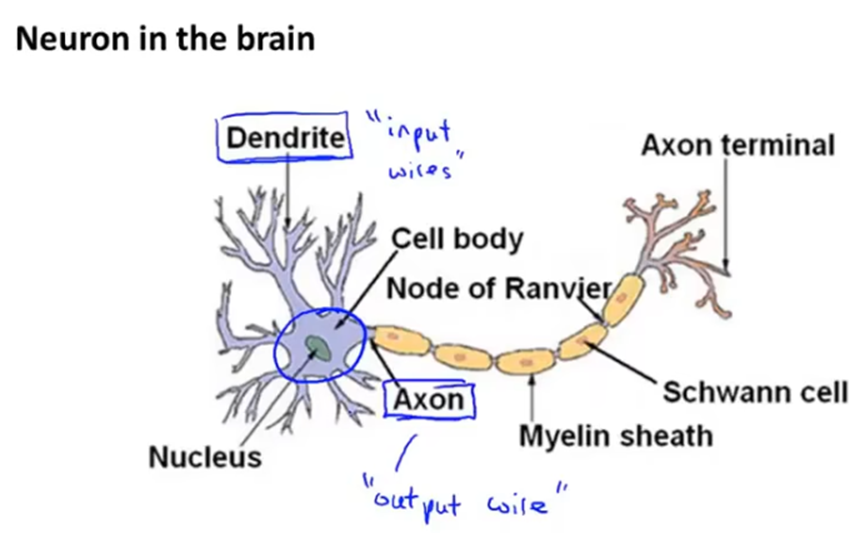
神经元结构如下,包括细胞体、树突、轴突等,树突用来接收其他神经元的信息,在细胞体进行处理后,使用轴突发送给其他神经元。
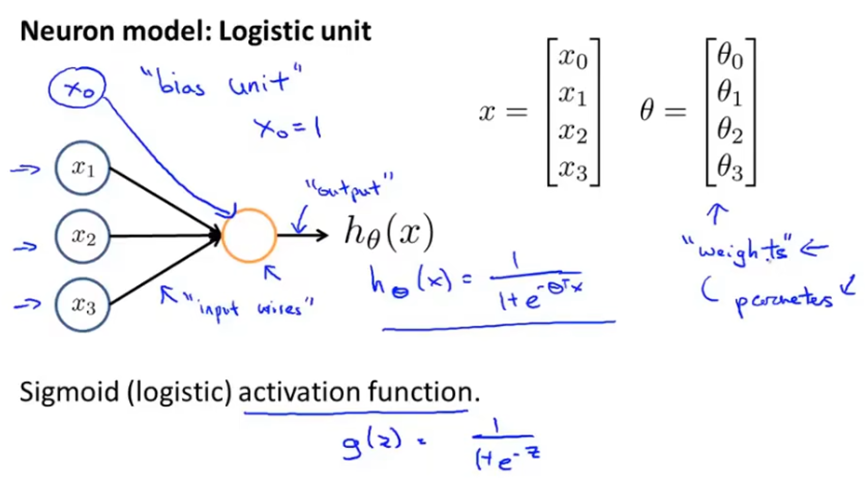
模拟的神经元模型如下,通过输入通道传递一些信息给它,然后神经元进行计算,并通过输出通道传递计算结果。其中x和θ是参数向量。
下图被称为一个带有sigmoid或者logistic激活函数的人工神经元。其中激活函数是指代非线性函数g(z)的另一个术语。
神经网络其实就是由一组神经元连接在一起的集合,如下。其中第一层被称为输入层,因为在这一层输入特征;最后一层被称为输出层,因为这一层的神经元输出最终结果;中间层被称为隐藏层,因为我们可以看到输入和输出,但中间的结果是隐藏的,隐藏层可以有多个。
应该注意的是,一般有一个x0单元没有画出,这个单元被称为偏置单元或偏置神经元,它的值始终是1。
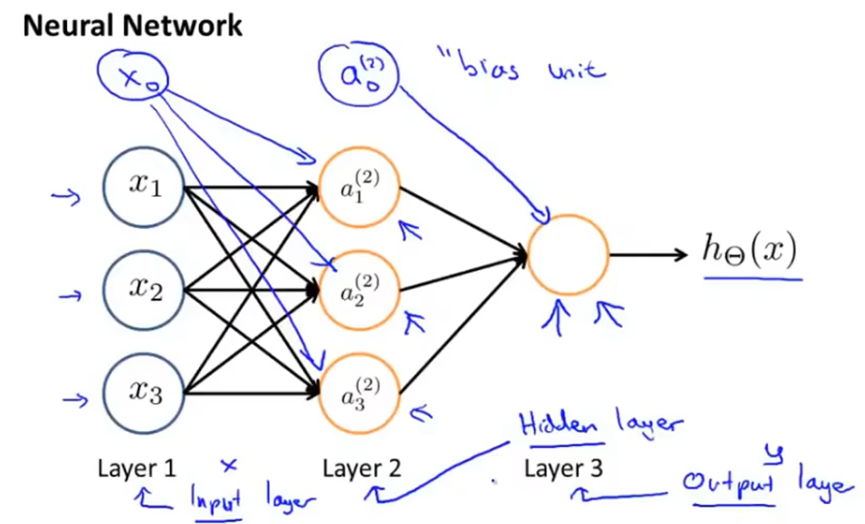
神经网络中,激活项ai(j)是指由一个具体神经元计算并且输出的值,这里上标j表示与第j层相关。
权重矩阵θ(j)用于将神经网络参数化,它控制着从第j层到j+1层的映射,如下图。θ(1)就是一个控制从三个输入单元到三个隐藏单元的映射的参数矩阵,是一个3*4矩阵(其中有一个未画出的x0单元)。
一般地,如果sj层有j个单元,sj+1层有j+1个单元,则矩阵θ(j)的维度就是(sj+1)*(sj+1)。
神经网络定义了函数h(x)从输入x到输出y的映射,即假设函数h(x),参数为θ,通过改变θ就能得到不同的假设。
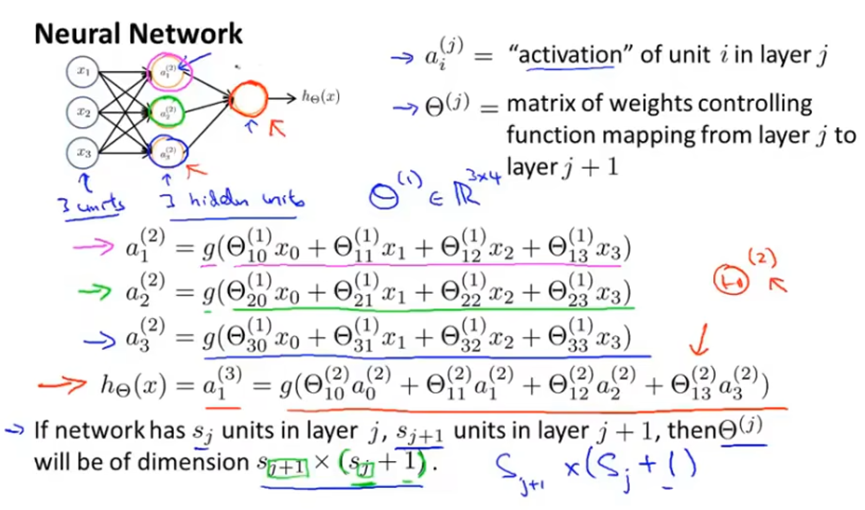
神经网络计算假设函数h(x)的过程,是一个前向传播的过程,从输入单元的激活项开始,前向传播给隐藏层,计算隐藏层的激活项,然后继续前向传播,计算输出层的激活项。
这一过程的向量化实现方法,首先将a(i)计算过程中,激活函数g的参数称为z(i),如a1(2)=g(z1(2)),z(i)是某个特定神经元的输入值x0,x1,x2,x3的加权线性组合。将x和z(2)定义为向量如下,可进行矩阵运算得到激活项a(2)。另外可以定义a(1)=x,将a(1)定义为输入层的激活项,计算z(2)和a(2)。然后a(2)添加上偏置单元a0(2)=1,使用a(2)计算z(3)和a(3)。
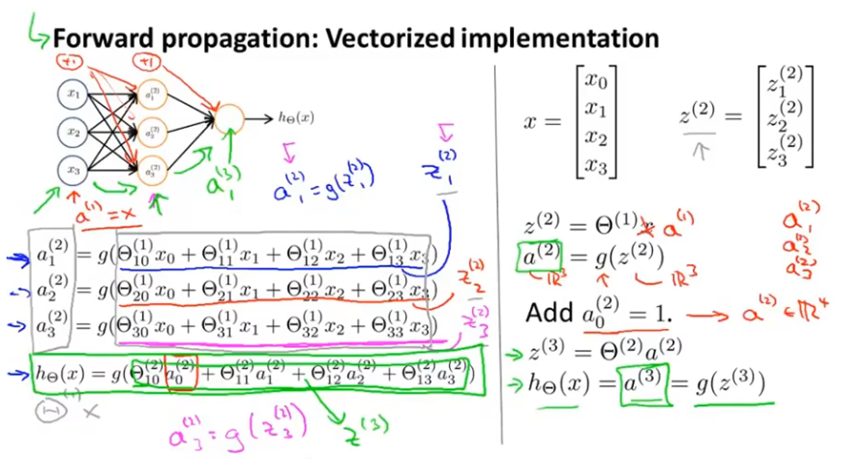
下图中,遮住输入层后,整个模型就是一个逻辑回归,不过特征是通过隐藏层计算的这些值。
这个逻辑回归模型中,特征是由输入层参数经过映射函数得到的,函数由参数θ(1)决定,也就是在神经网络中,它自己训练逻辑回归的输入,因此如果改变θ(1)可能会学习到一些很复杂的特征。
神经网络中神经元的连接方式称为神经网络的架构
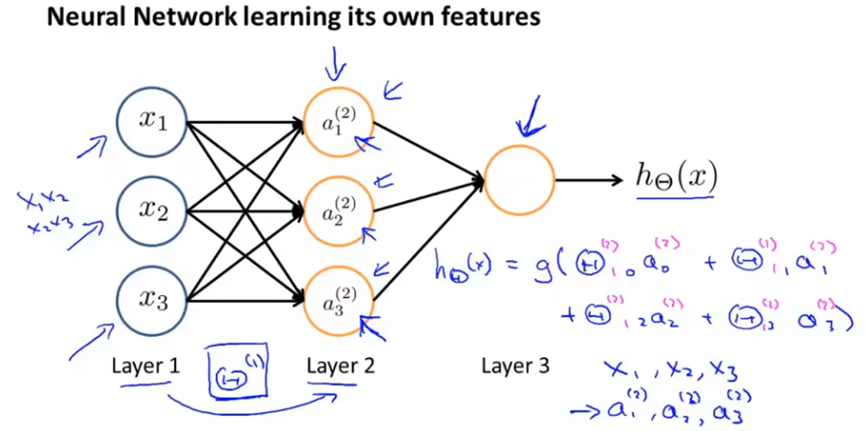
神经网络的简单例子如下,通过设置参数θ,可以得到等价为与运算的假设函数。其中g(x)是激活函数,当x趋向于正无穷时,g(x)趋向于1,当x趋向于负无穷时,g(x)趋向于0。
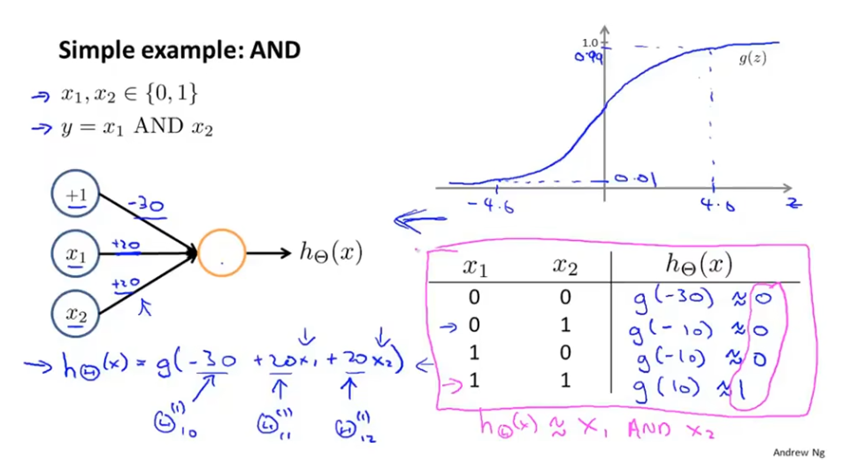
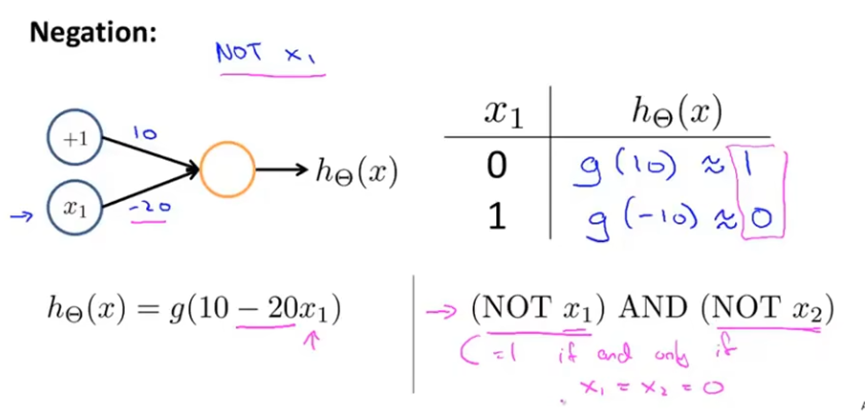
要得到非x1,就在x1前面加一个很大的系数,并且x0的系数需要是正的。
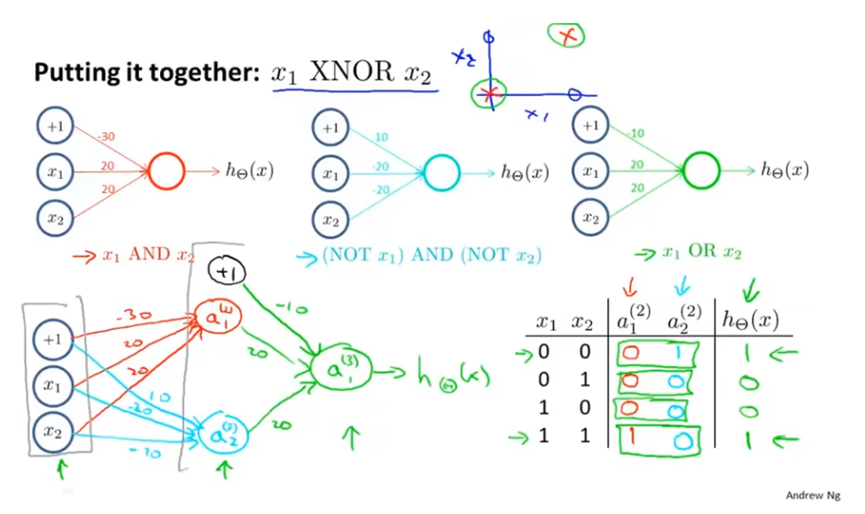
将输入放在输入层,在隐藏层计算一些关于输入的略微复杂的功能,然后再增加一层,用于计算一个更复杂的非线性函数。(这图有点像逻辑电路)
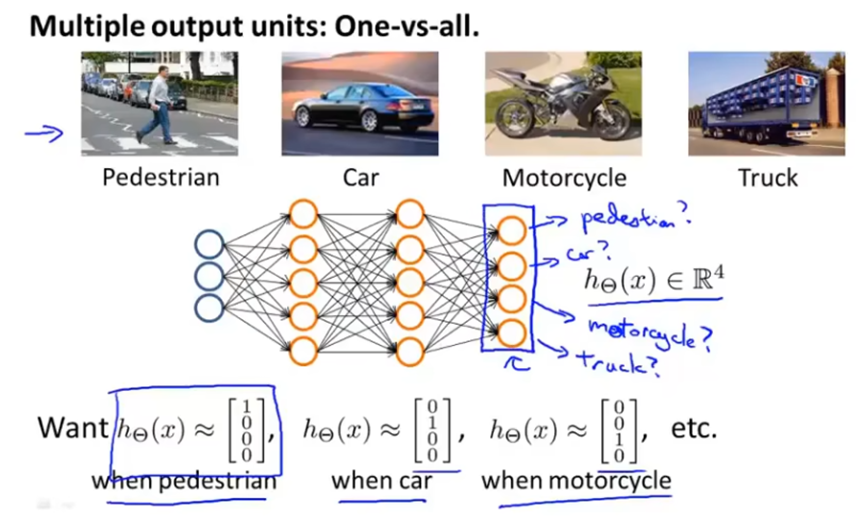
多元分类,建立有多个输出单元的神经网络,每个输出单元分别用于判断不同的结果。
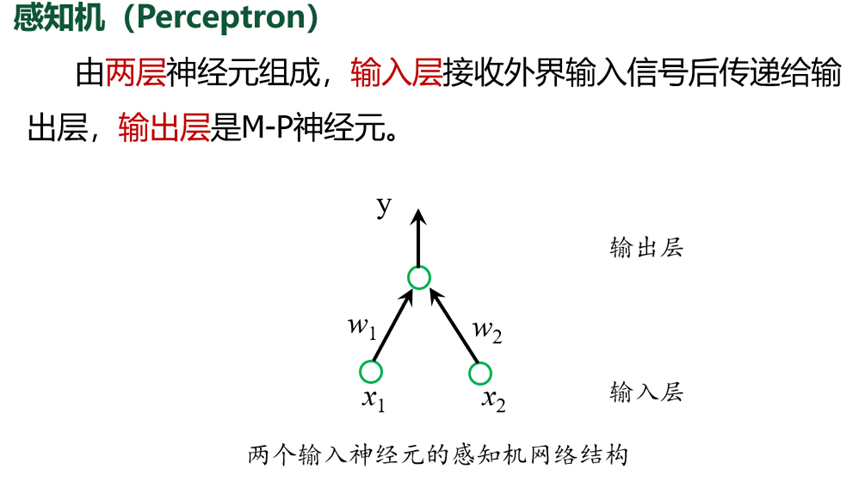

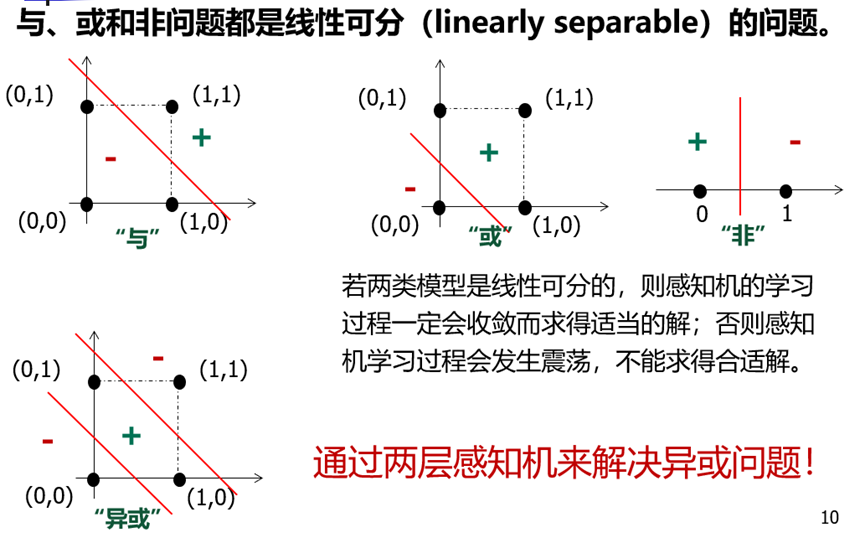
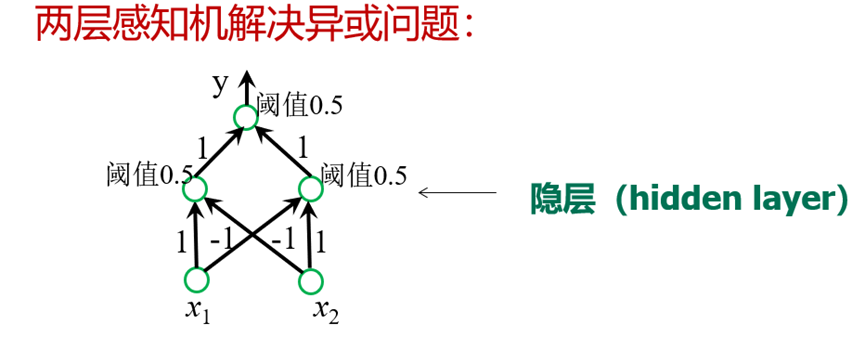
SVM支持向量机
SVM的代价函数曲线例如下图,和逻辑回归相比,是使用两段直线。

SVM的代价函数相比逻辑回归,删掉了一个系数1/m,并且正则化项前的正则化参数λ换成代价函数前的C。并且将原来的log项换成cost1和cost2。
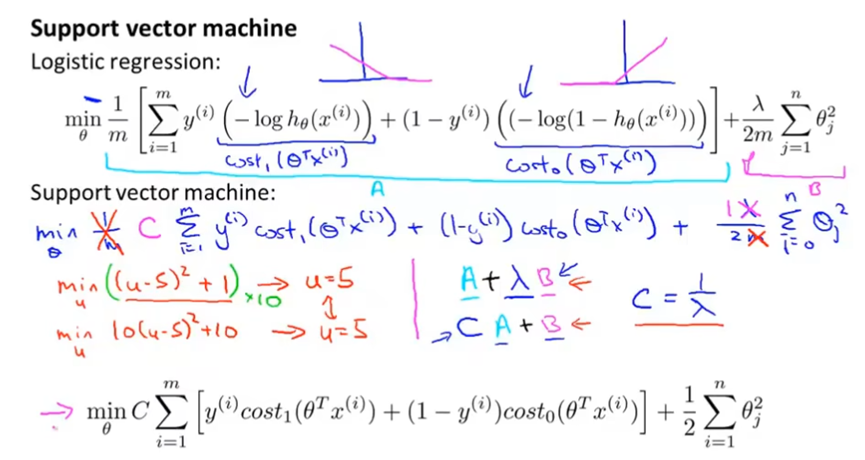
支持向量机也被称为大间距分类器。
对于一个正样本,只有z>=1时,代价才为0。
对于一个负样本,只有z<=-1时,代价才为0。

当C设置很大时,最小化SVM的代价函数,会倾向于找到一个参数使得代价函数中的第一项为0,这时当y=1时,θTx>=1,当y=0时,θTx<=-1。从而可以得到一个很有趣的决策边界。如图,黑线是SVM得到的决策边界,显然黑线与训练样本的最小距离更大,即拥有更大的间距。

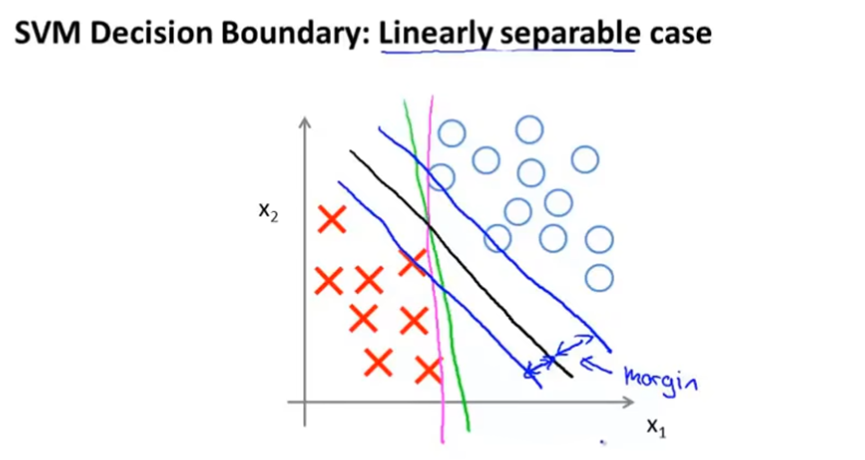
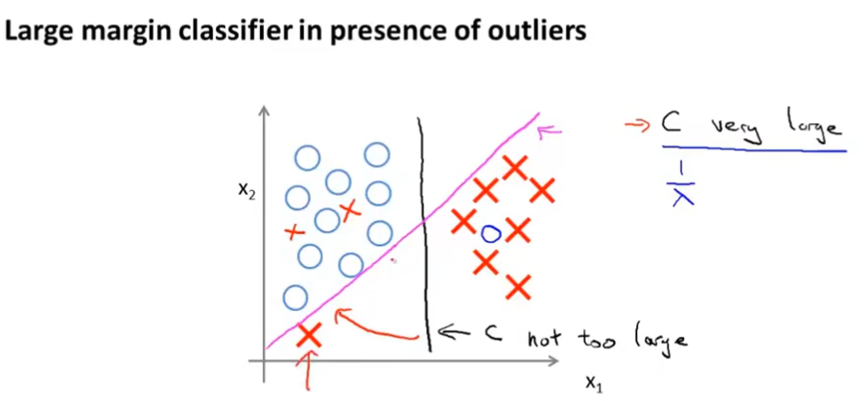
但是当C设置很大,只使用大间距分类器的话,对异常点会很敏感。当C不是非常大时,可以忽略这些异常点。
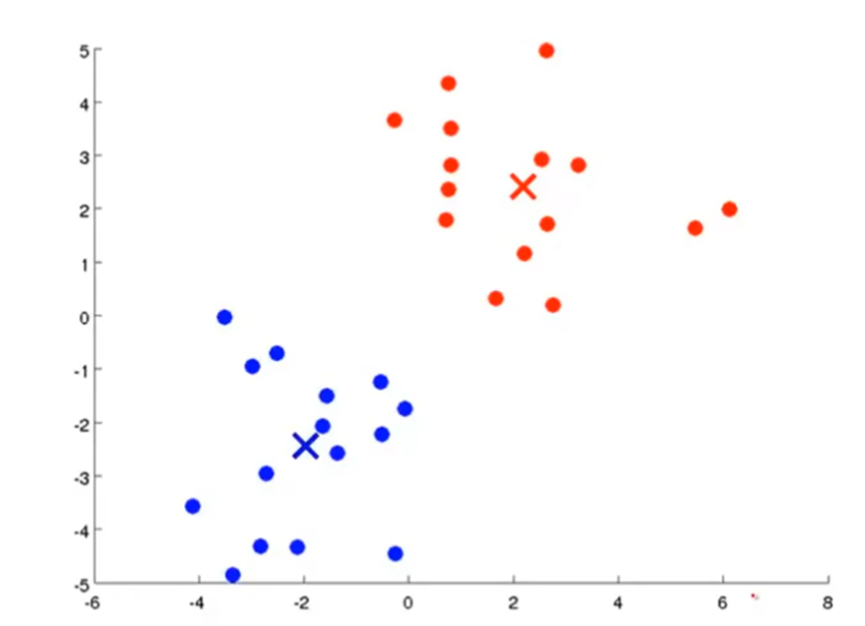
聚类
聚类算法属于无监督学习,如k-means算法。K-means算法步骤如下:
要将数据分为两类,首先随机生成两点作为聚类中心。
k-means重复进行两个步骤:1.簇分配,2.移动聚类中心。
簇分配是遍历每个样本,根据样本和两个聚类中心的距离判断,将样本分配给较近的聚类中心。
移动聚类中心是计算两个聚类的平均位置,将聚类中心移动到新的平均位置处。
重复进行这两个步骤,直到聚类中心不再发生变化时,认为已经聚合了。
k-means算法的输入为:1.簇的数量K,2.训练集


k-means优化目标函数(最小化代价函数)是对xi到μci距离的平方求和。参数ci表示
xi所属的簇的序号,μk表示第k个聚类中心的位置。μci表示xi所属的簇的聚类中心位置。K-means就是要找到参数ci和μi,使得代价函数最小。

簇分配通过修改xi来最小化代价函数,移动聚类中心是通过修改μci来最小化代价函数。
随机初始化聚类中心的方法。
首先应该保证簇的数量K<样本数量m。
然后随机挑选K个训练样本,令聚类中心μi等于这K个样本。

但是根据随机挑选的K个训练样本不同,k-means可能落在局部最优。
我们可以多次初始化并运行k-means算法,从而得到一个尽可能好的局部或全局最优值。如执行100次k-means算法,然后再选择代价最小的一个。应该注意,当K小的时候运行多次算法可以很好地最小化代价函数,当K很大时候则通常不会有多少改善。
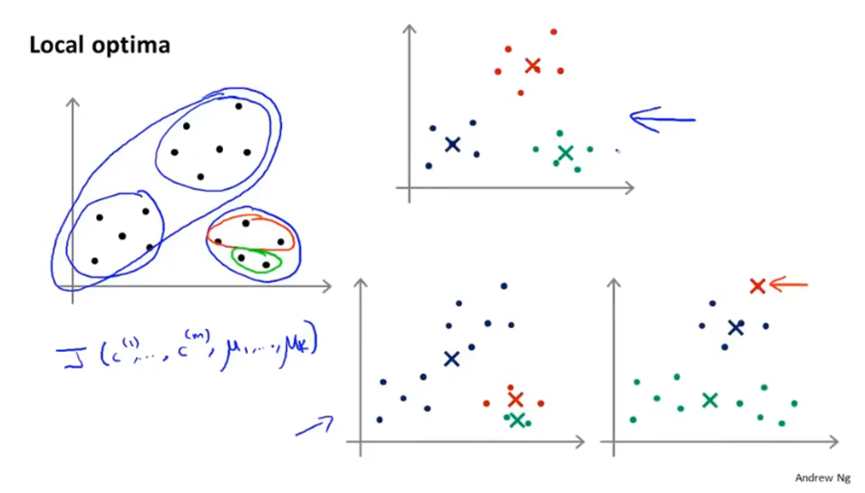

选择聚类数量K的方法。最常见的还是通过观察可视化的图,手动选择K的值。
这里介绍一种方法称为肘部方法。从1开始逐渐增加K的值,并且计算代价函数,画出对应的曲线,观察曲线的肘部,即一个阈值,将该阈值设置为K。但通常得到的曲线不好判断肘部。
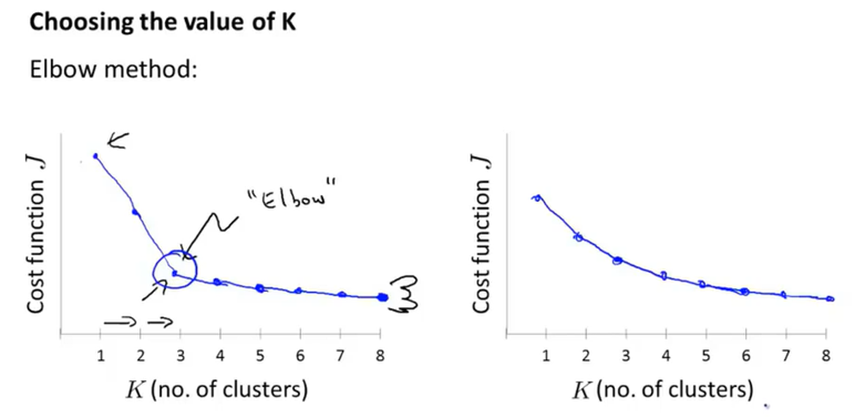
另一种方法是结合聚类算法的下游需求,比如要给三件衣服做分类,K就是3。
推荐系统
推荐系统用于向用户推荐他们可能感兴趣的事物。
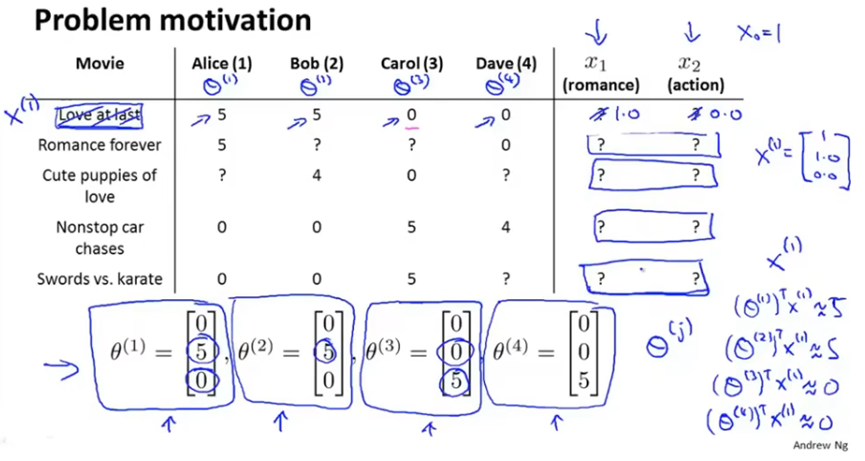
基于内容的推荐算法,如下例,预测用户对电影的评分。
首先nu表示用户数量,nm表示电影数量。
假设每部电影都有一个对应的特征集,这里假设有x1和x2,x1衡量爱情片程度,x2衡量动作片程度。并且加入一个额外特征x0=1,称为截距特征。从而对每部电影都会有一个特征向量x(i)。用n表示特征数量,这里n=2。
可以将每个用户的评价预测值看作一个线性回归问题,对每个用户,需要学习一个参数向量θ(j),参数向量是n+1维的。
学习到一个用户的参数向量θ(i)后,计算(θ(i))(T)x(j)就能得到用户i对电影j的评价预测值。

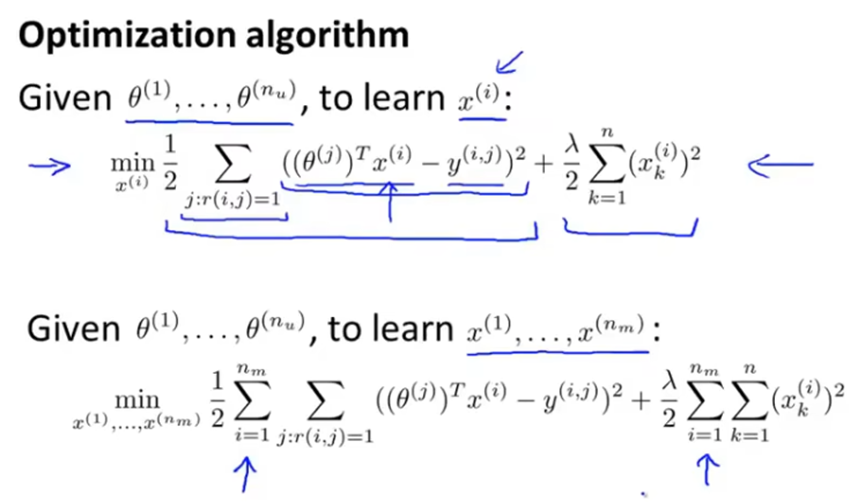
用于学习θ的代价函数如下。
r(I,j)表示用户j是否有对电影i评分,y(I,j)表示用户j对电影i的评分值。i:r(I,j)=1表示所有用户j评分过的电影。

代价函数由方差项和正则化项组成。要学习所有用户的参数,需要在前面再加一个对所有用户的求和,并且最终最小化这个总体代价函数。

推荐系统的另一种方法是协同过滤。
协同过滤算法有一个特征学习的特性,可以自行学习要使用的特征。
假设不知道电影的特征值x(i),但知道每个用户的参数θ(j)(各种电影的喜爱程度,问卷等方法)。用每个用户的参数向量θ和用户对电影的评分就能推断出电影的特征值。
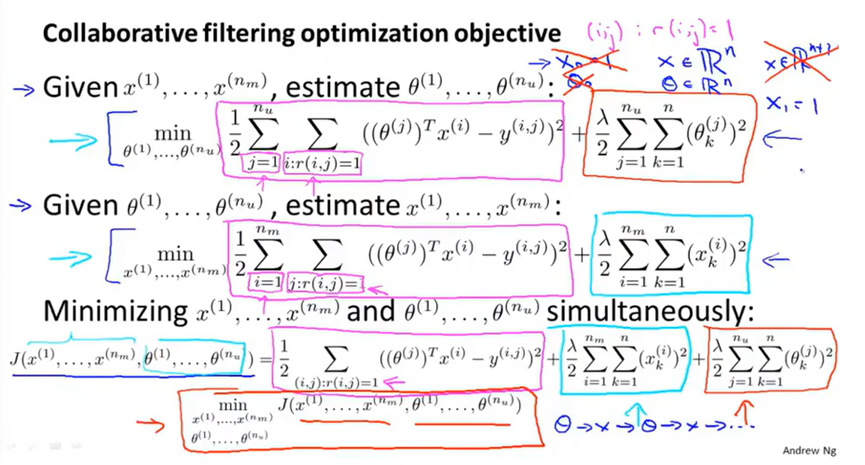
协同过滤的代价函数如下,已知参数向量θ(i),要学习特征向量x(i),即是要得到当代价函数最小化时特征x(i)的取值。由一个平方误差项和一个正则化项组成,正则化项用于防止特征值变得太大。要学习所有电影的特征向量,所以在前面加上对所有电影的求和。
所以这里是通过给定的参数向量θ来学习特征向量x,而之前提到的是通过给定的特征向量x来学习参数向量θ。其实我们可以先随机化一个参数向量θ,然后通过θ学习x,再通过x学习θ,再通过θ学习x,以此类推,直到收敛到一组合理的θ和x。
但其实存在一个更有效率的算法,不需要重复计算x和θ,而是可以将x和θ同时计算出来。代价函数如下,如果将x都设置为常数,然后求j关于θ的最小值的话,相当于计算第一个公式;如果将θ设置为常数,然后求j关于x的最小值的话,相当于计算第二个公式。
我们将这个代价函数视为特征x和用户参数θ的函数,同时进行最小化。
使用这种形式学习特征值时,不需要额外特征x0,特征向量为n维。参数向量同样是n维,不需要θ0。
所以协同过滤算法步骤如下:
首先初始化x和θ为小的随机值。
然后使用梯度下降或者其他优化算法将代价函数最小化。
最后对于一个用户的参数向量θ和电影的特征向量x,可以预测用户对电影的评分。

可以将评分y,特征值x,用户参数θ,预测评分都作为一个矩阵。用矩阵运算来计算预测评分。这个协同过滤算法也叫做低秩矩阵分解。
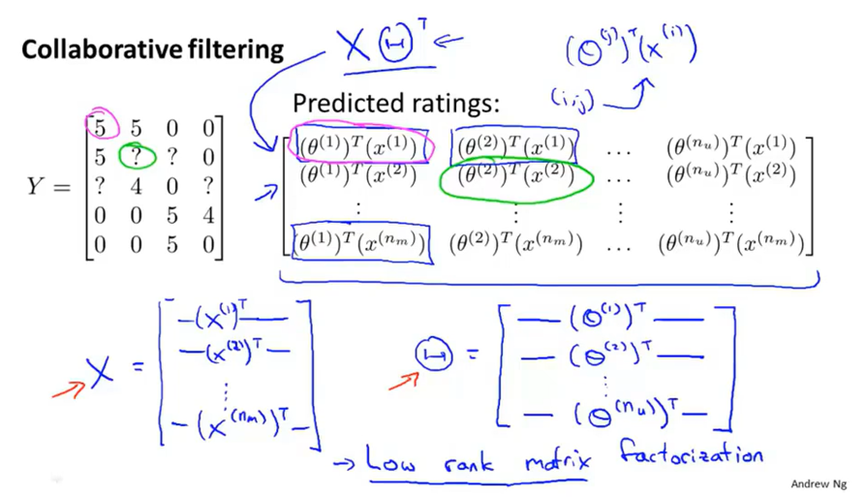
协同过滤算法中,如果一个用户没有对任何电影做出评价,那么他的参数值会都是0,对任何电影的预测结果也都是0。
可以使用均值归一化解决这个问题。计算每个电影所得评分的均值,把它放在μ向量中。然后将原始评分减去均值,使得每个电影的平均评分都是0。用这些新评分作为训练集学习θ和x。
预测用户评分时,用得到的θ和x内积再加上μi。这样对于没有评价过电影的用户,他的预测结果也是平均评分μi,而不是0。

系统设计
比如用于垃圾邮件检测,我们选择一些重点词汇作为特征,如选择100个词,就有100维的特征。然后对每个邮件样本进行数据预处理,得到它的特征向量。用这些特征向量作为样本训练模型。

性能评估
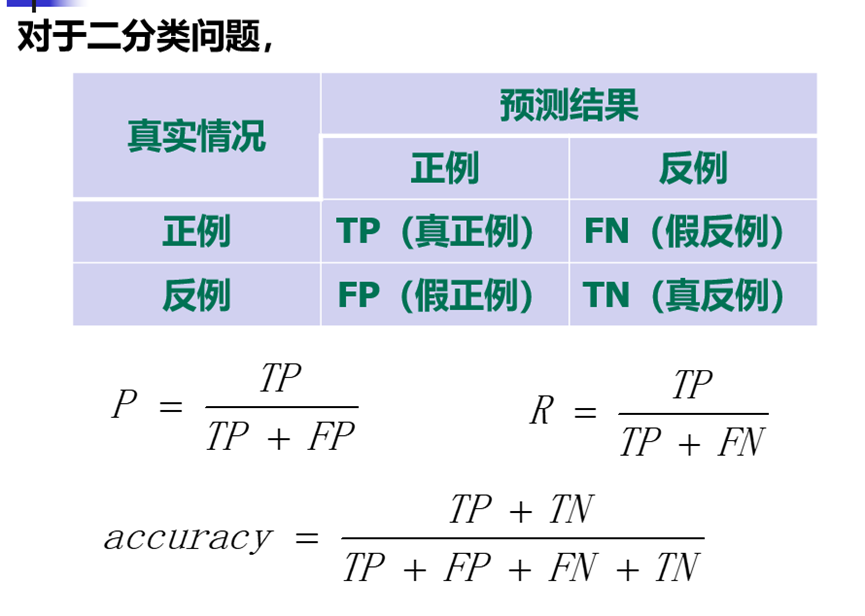
准确率:分类正确的样本数占样本总数的比例。
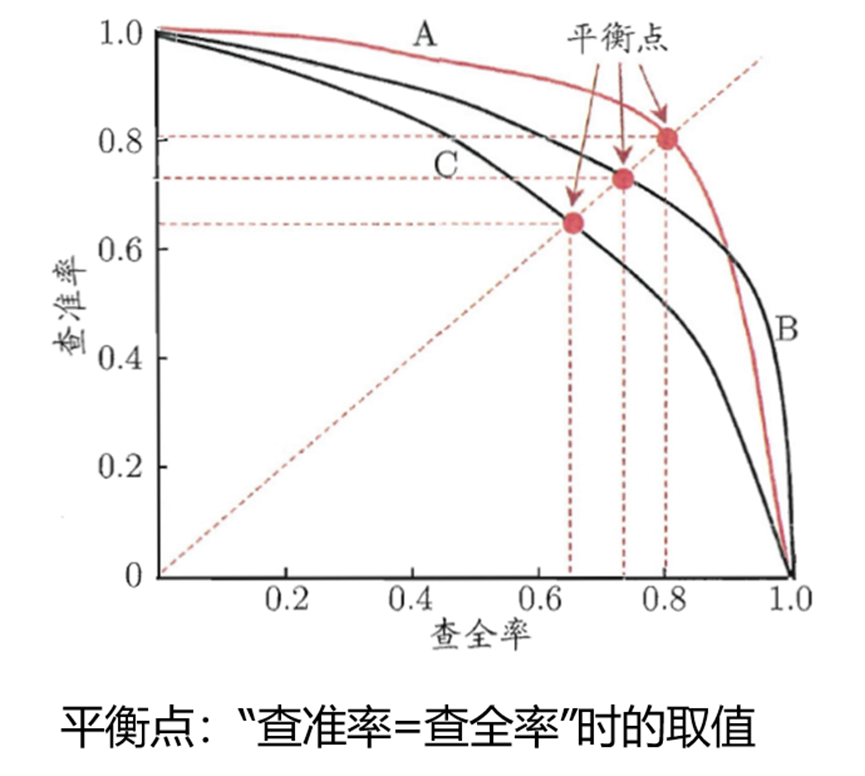
查准率(精确率):检索到结果中有多少是正确的。
查全率(召回率):所有正确结果中有多少被检索出来了。
F1:既能体现精确率又能体现召回率的一个评价指标。
下面为混淆矩阵,以及各性能计算。


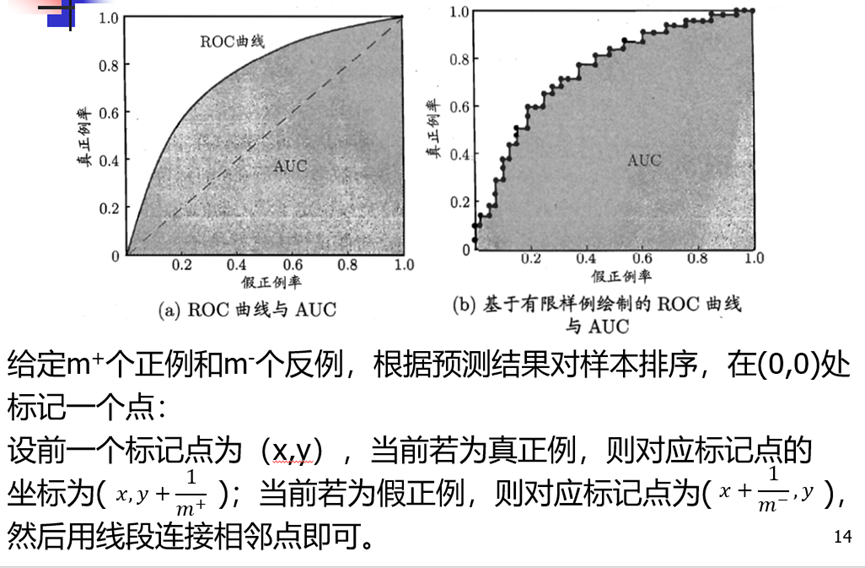
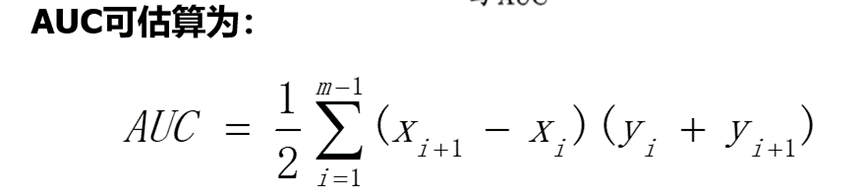
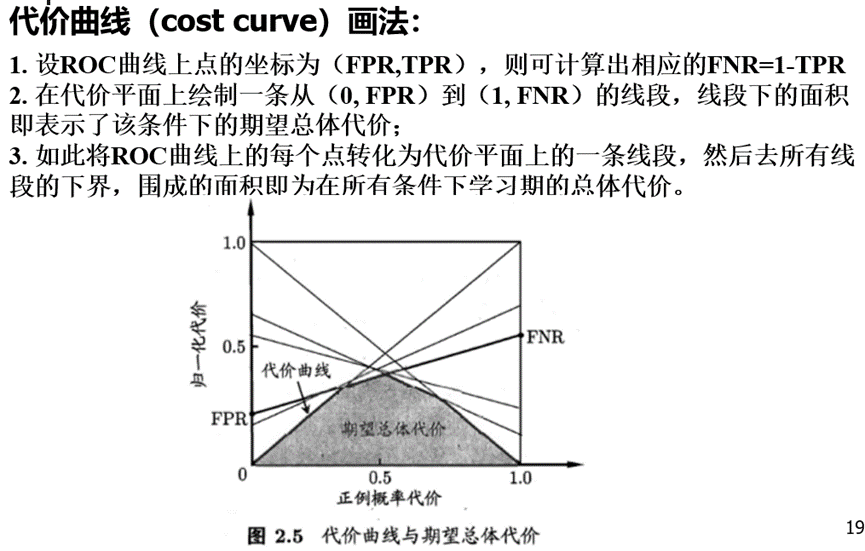
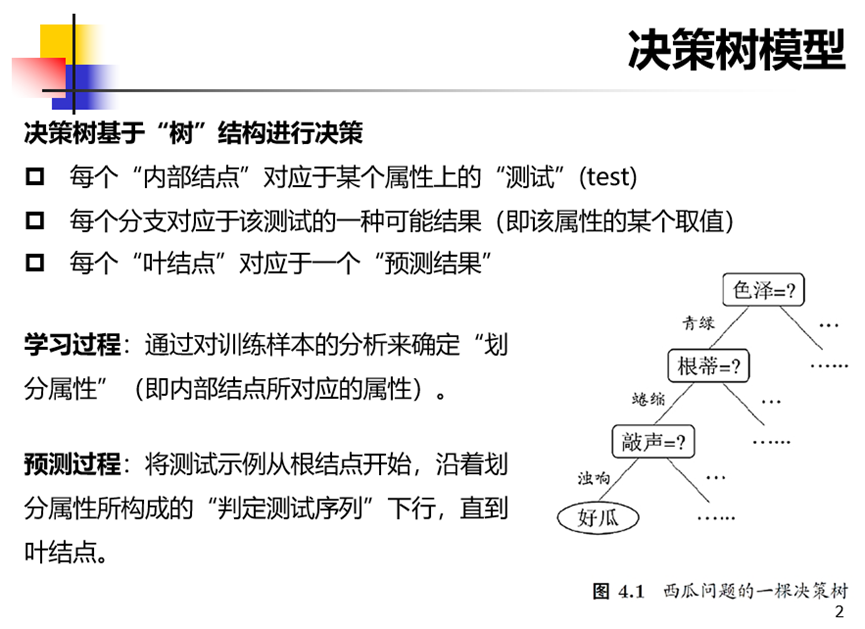
决策树

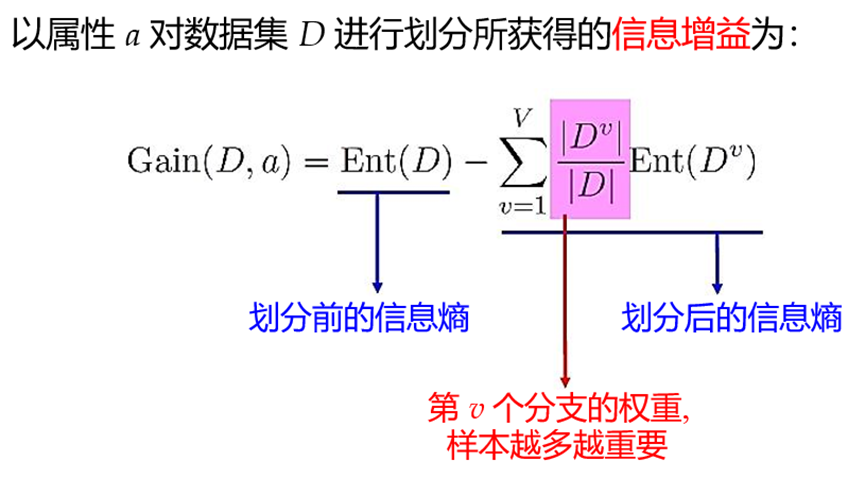
划分属性,三种方法:信息增益、增益率、基尼指数
信息增益:计算每个属性的信息增益,选择信息增益最大的作为划分属性。缺点:信息增益对可取值数目较多的属性有偏好。
增益率:缺点:对取值数目较少的属性有偏好。C4.5 算法中使用启发式:
先从候选划分属性中找出信息增益高于平均水平的,再从中选取增益率最高的。
基尼指数:选择基尼指数最小的属性,反映了从 D
中随机抽取两个样例,其类别标记不一致的概率。
信息增益计算例子:

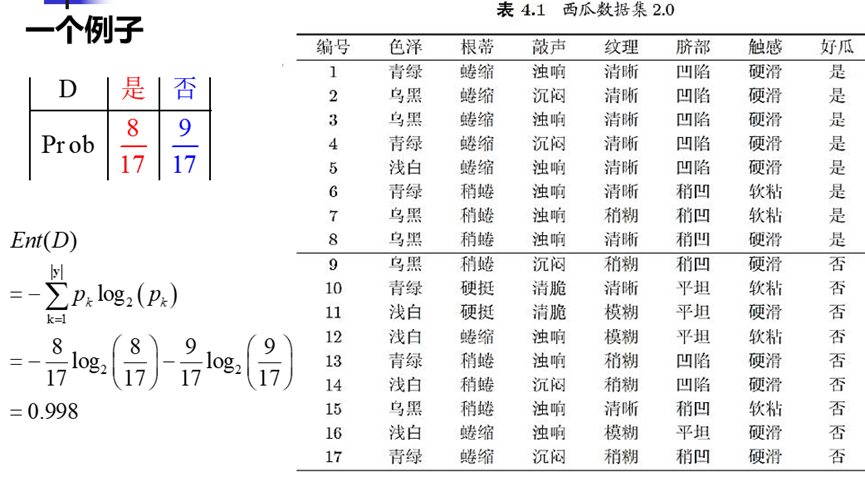




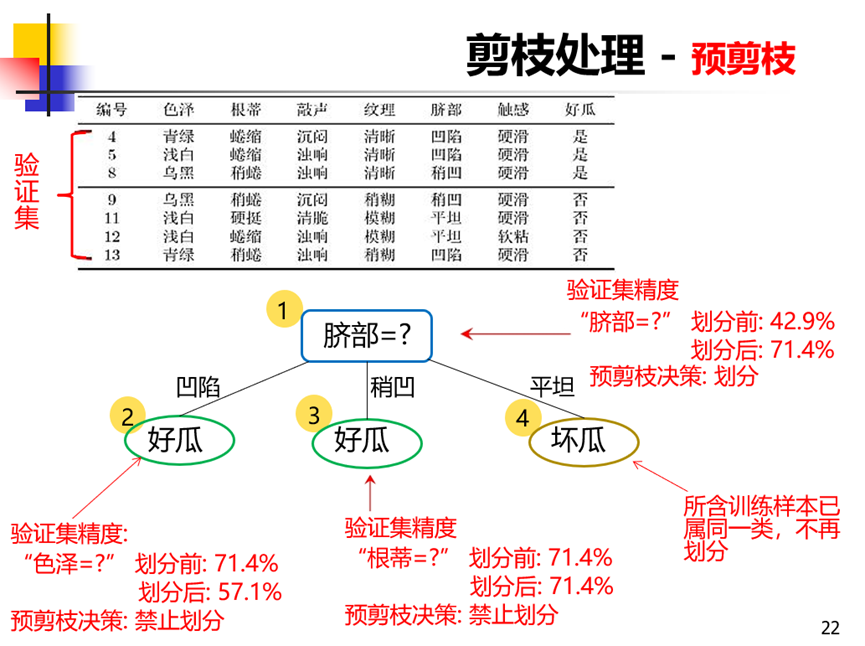
预剪枝:生成过程中,对每个结点划分前进行估计,若当前结点的划分不能提升泛化能力,则停止划分,记当前结点为叶结点。叶节点类别为之前该子树中样本数量较多的类别。
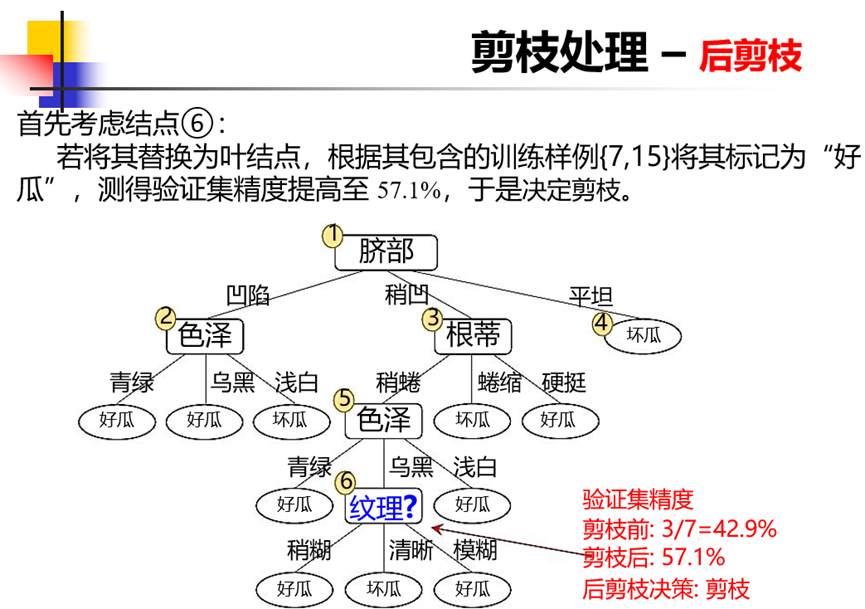
后剪枝:生成一棵完整的决策树后,从底部向上对内部结点进行考察,如果将内部结点变成叶结点,可以提升泛化能力,那么就进行交换。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号