网络与系统安全 - 课程笔记
对称与非对称密码的优缺点
对称密码
优点：
- 加解密速度快
- 易于硬件实现
- 密钥相对较短，易于传输
缺点：
- 密钥分配问题，密钥分发困难，需要安全信道
- 密钥管理问题，密钥量大，多人使用时，每两个用户都需要生成一个对称密钥
- 没有签名功能，存在身份认证问题，接收方可能伪造信息
非对称密码
优点：
- 密钥分配简单，不需要安全信道
- 密钥管理简单，一个用户仅需要保护自己的一个私钥
- 可以进行数字签名，实现身份认证和完整性校验
缺点：
- 加解密速度相对较慢
- 密钥相对较长
- 存在公钥的身份认证问题
密码学发展阶段
第1阶段：1949年以前
1949年以前的密码技术可以说是一种艺术，而不是一种科学，那时的密码专家是凭直觉和信念来进行密码设计和分析的，而不是靠推理证明。
第2阶段：从1949年到1976年
1949年Shannon发表的《保密系统的通信理论》一文，标志着密码术到密码学的转变。
第3阶段：1976年至今
1976年Diffie和Hellman发表了《密码学新方向》一文，提出了一种崭新的密码设计思想，导致了密码学的一场革命。
OSI安全框架
- 安全攻击：任何危及系统信息安全的活动。
- 安全机制：用来保护系统免受侦听、阻止安全攻击及恢复系统的机制。
- 安全服务：加强数据处理系统和信息传输的安全性的一种服务，利用一种或多种安全机制阻止安全攻击。
安全攻击
攻击类型分为：被动攻击和主动攻击
被动攻击
类型可分为：
- 消息内容泄露
- 流量分析
常见手段：
- 搭线监听
- 无线截获
- 其他截获（非法拷贝等）
主动攻击
通常分为：
- 假冒
- 重放
- 篡改消息
- 拒绝服务
安全机制
特定的安全机制：加密、数字签名、访问控制、数据完整性、认证交换、流量填充、路由控制等。
普遍的安全机制：可信功能、安全标签、事件检测、安全审计跟踪、安全恢复等。
安全服务
- 认证
- 访问控制
- 数据保密性
- 完整性
- 不可否认性
- 可用性
网络安全模型
设计安全服务应包含四个方面内容 ：
- 设计执行安全相关传输的算法
- 产生算法所使用的秘密信息
- 设计分配和共享秘密信息的方法
- 指明通信双方使用的协议，该协议利用安全算法和秘密信息实现安全服务
邮件安全
邮件消息不安全的原因：
- 在传输的过程中可以被监视
- 也可能被目标系统中的特权用户所监视
- 有点像“明信片”
安全性增强：
- 机密性：保护以不被破译
- 可认证：可对消息的发送方进行认证
- 完整性：保护以不被篡改
- 不可否认性：抗发送方的否认
防火墙
两个基本设计方针：
- 没有明确允许的都是被禁止的
- 没有明确禁止的都是被允许的
设计目标：
- 所有通信都必须经过防火墙
- 只有被授权的通信才能通过防火墙
- 对于渗透必须是免疫的
局限性：
- 防火墙防外不防内
- 不能防范绕过防火墙的攻击
- 防火墙配置复杂，容易出现安全漏洞
- 防火墙往往只认机器（ IP 地址）不认人（用户身份），并且控制粒度较粗
- 防火墙不能防范病毒
- 防火墙不能防止数据驱动式攻击
分类：
- 包过滤路由器
- 应用级网关
- 电路级网关
恶意软件
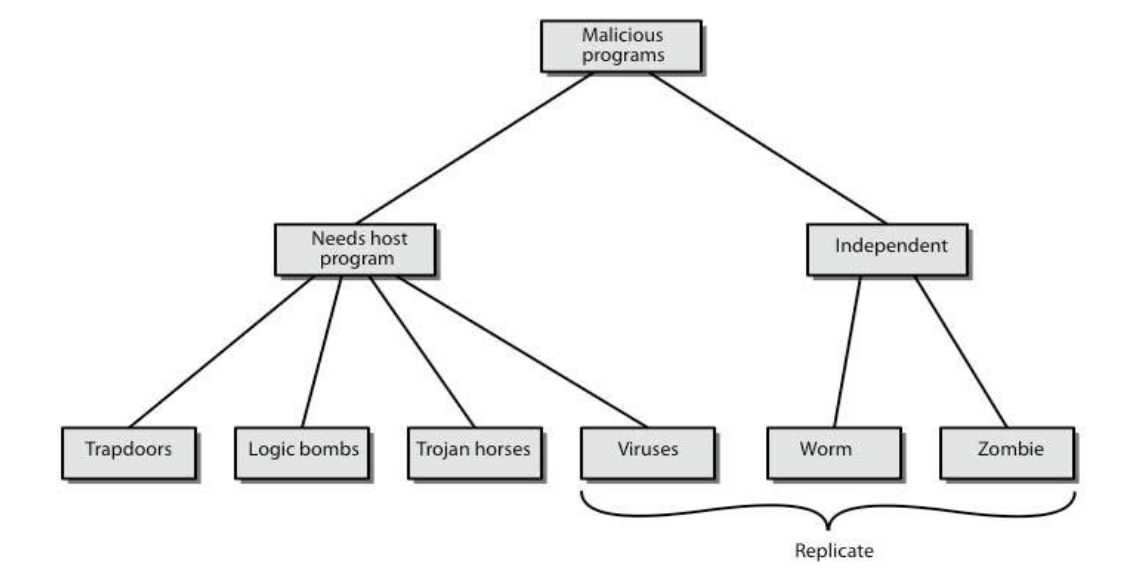
恶意软件分类：
- 后门（陷门）
- 逻辑炸弹
- 特洛伊木马
- 病毒
- Zombie（肉机）
- 蠕虫
病毒和蠕虫的状态：
- 潜伏阶段
- 传染阶段
- 触发阶段
- 发作阶段
希尔密码
希尔密码是运用基本矩阵论原理的替换密码,使用一个m*m的矩阵作为密钥，此矩阵必须可逆，解密使用逆矩阵解密。
方阵的行列式非零(mod 26)，且行列式与26互素，则方阵可逆。
方阵的秩等于它的阶数，则方阵可逆。明文分成长度为 m 的向量
密文向量=密钥矩阵*明文向量 (mod 26)
明文矩阵=密钥矩阵逆矩阵*密文向量 (mod 26)
希尔密码的逆矩阵不是通过常见的方法求出来的。因为一般初等行变换求逆，得到的逆矩阵元素很多都是分数，而希尔密码的逆矩阵元素是整数。当初等行变换得到的逆矩阵元素都是整数时，和希尔密码的逆矩阵相同。参考该链接：关于希尔密码的简单研究
如对以下矩阵：
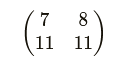
其逆矩阵是：
但希尔密码中其逆矩阵是：
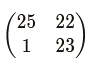
一般逆矩阵的计算公式如下：
其中A为矩阵，\(A^{−1}\) 为 A的逆矩阵，\(A^*\)是A的伴随矩阵，|A|是A的行列式。
而希尔密码密钥矩阵的逆矩阵计算公式如下：
其中\(|A|^{-1}\)表示A的行列式的模逆，这里模数为26。
计算模逆的方法：
1.枚举：
2.拓展欧几里得算法
(1) 列表法
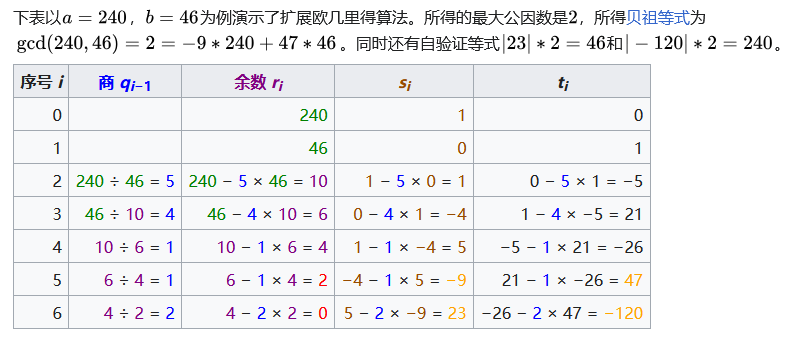
扩展欧几里得算法 - 维基百科，自由的百科全书 (wikipedia.org)
(2) 先算550,1759的最大公因数，然后再逆推回去，得到550x%1759=1，则x就是逆元。
计算伴随矩阵：
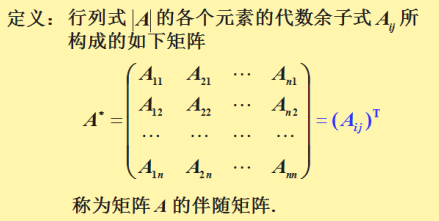
初等行变换求逆矩阵：
