circle 题解

题意简述：

• \(n\)个圆，圆心都在\(x\)轴上，并且圆心坐标和半径均为整数，同时保证圆不相交（但显然是可以相切的）

• 求这\(n\)个圆将平面（可视为无限大）分为了几部分

• 数据范围：

  • 对于50%数据，\(n<=5000\)且\(x[i]+r[i]<=10^6\)，\(x[i]-r[i]>= - 10^6\)

  • 对于100%数据，\(1<=n<=300000\),\(-10^9<=x[i]<=10^9,1<=r[i]<=10^9\)

  • 数据保证圆与圆不重合。

---

题目分析：

• 我们很容易想到\(n\)个圆（在题意理解下）至少将平面分成\(n+1\)个部分，那么容易想到这种情况：

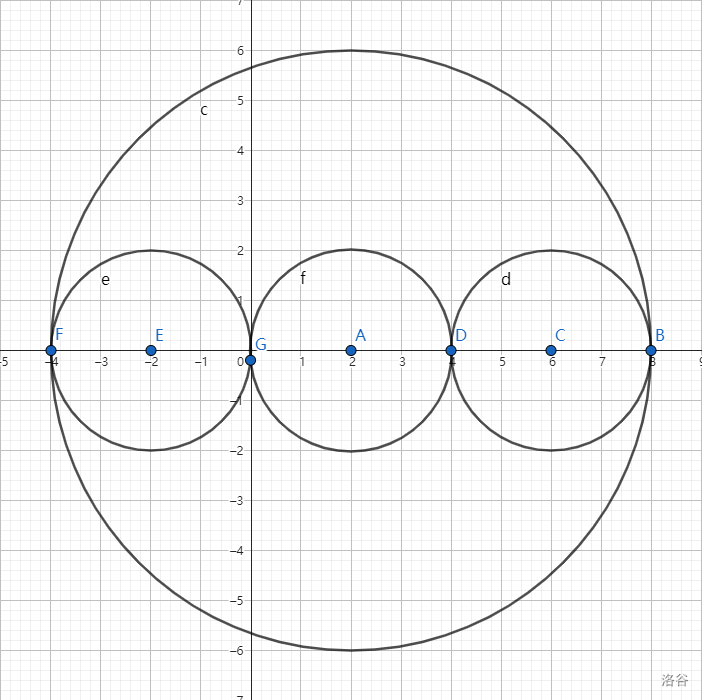
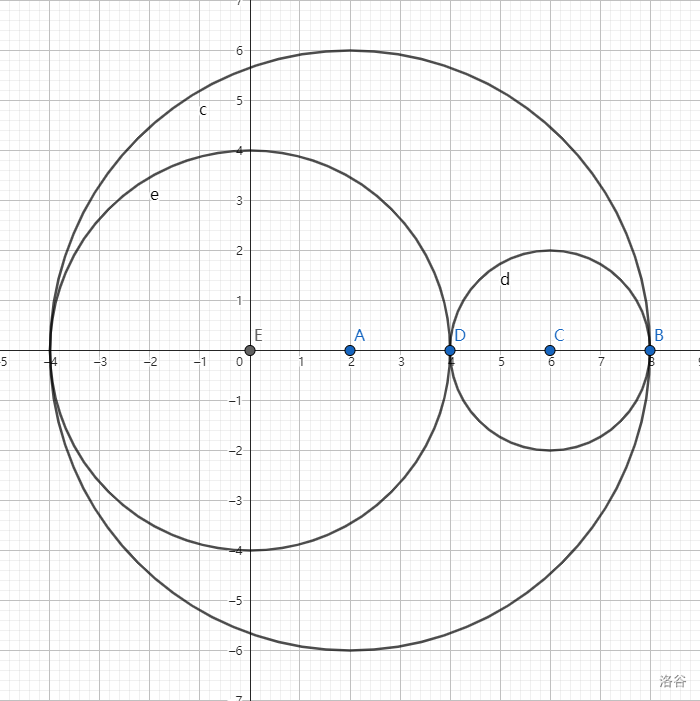
（图片来自victoryang的博客）

• 这种情况之下，大圆被分成了上下两部分，总答案加一

• 那么问题就变成了我们要看多少个圆能被正好分成上下两部分

---

思路：

• 我们可以记录每个圆的左右端点（即左右分别与\(x\)轴的交点，以下为了方便称为端点）的坐标

• 同时记录一下该圆的大小，该点是左端点还是右端点，该点所属圆的编号

• 为什么呢？因为我想要把所有点排个序

  • 首先怎么排：

    • 这个圆的左右端点排序之后中间包含的一定是这个大圆里面所有的小圆

  • 那么在排序的时候要注意很多东西，主要问题在两个点重合怎么办

    • 两个点重合，分别是两个圆的左右端点：将右边圆的右端点排在前，左边圆的左端点排在后

    • 同为两个圆的左/右端点：将大圆排在外面（大圆的左端点靠前，右端点靠后）

• 排序之后就可以\(dfs\)了

  • 从这个圆的左端点\(+1\)处（排序编号，不是坐标）开始找，找到一个圆继续\(dfs\)这个圆，同时外面的大圆找的编号直接跳到这个小圆的右端点即可，记录一下跳的圆是否连贯，最终能否到达右端点即可。如合法，答案\(+1\)

总复杂度\((nlogn)\)，但由于\(dfs\)是\(O(n)\)的，所以跑得飞快，甚至比std快

---

代码

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#define int long long
#define maxn 300005
using namespace std;
void read(int &n){
	n=0;int f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-') f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		n=(n<<3)+(n<<1)+ch-'0';
		ch=getchar();
	}
	n*=f;
}

int n;
struct node{
	int x,l,fro;bool pd;
	friend bool operator < (node aaa,node bbb){
		if(aaa.x==bbb.x){
			if(aaa.pd==false){
				if(bbb.pd==false){
					return aaa.l > bbb.l;
				}else{
					return bbb.pd < aaa.pd;
				}
			}else{
				if(bbb.pd==true){
					return aaa.l < bbb.l;
				}else{
					return aaa.pd > bbb.pd;
				}
			}
		}else{
			return aaa.x < bbb.x;
		}
	}
}pl[maxn<<1];
int st[maxn],ed[maxn];
int ll[maxn],rr[maxn];
int ans=0;

void dfs(int _st,int _ed,int stpl,int edpl){
	bool flag=false;
	int j=stpl;
	for(int i=_st+1;i<_ed;i){
		if(ll[pl[i].fro]!=j) flag=true;
		dfs(st[pl[i].fro],ed[pl[i].fro],ll[pl[i].fro],rr[pl[i].fro]);
		j=rr[pl[i].fro];
		i=ed[pl[i].fro]+1;
	}
	if(flag==false&&j==edpl) ans++;
}

signed main()
{
	freopen("circle.in","r",stdin);
	freopen("circle.out","w",stdout);
	read(n);
	int x,r;
	for(int i=1;i<=n;i++){
		read(x),read(r);
		pl[(i<<1)-1]=(node){x-r,r<<1,i,false};
		pl[i<<1]=(node){x+r,r<<1,i,true};
	}
	sort(pl+1,pl+(n<<1)+1);
	for(int i=1;i<=(n<<1);i++){
		if(pl[i].pd==false){
			st[pl[i].fro]=i;
			ll[pl[i].fro]=pl[i].x;
		}else{
			ed[pl[i].fro]=i;
			rr[pl[i].fro]=pl[i].x;
		}
	}
	dfs(0,(n<<1)+1,pl[1].x-1,pl[(n<<1)].x+1);
	ans+=n+1;
	printf("%lld",ans);
	return 0;
}

---

原发布于 \(2023.2.7\)