Factorization Machines 因子分解机
Factorization Machines (FM)

首先这种算法是一种有监督的机器学习模型,既可以用在分类问题也可以用在回归问题当中,它是一种非线性的模型,相比逻辑回归具备了二阶交叉特征表达能力(不易拓展到三阶以上)。可以通过stochastic(随机) gradient descent (SGD), alternative least square (ALS), or Markov chain Monte Carlo (MCMC)方法进行训练。这种算法某种程度算作SVD算法的拓展,可以将稀疏向量表达的某一维特征转换为隐稠密向量(通过学习得出,在某些神经网络中充当embedding层便于网络接入),两个稠密向量的内积是他们的权重。它的变种为field-aware factorization machines (FFM),提高了特征交叉能力,但是复杂度达到O(n^2)。
组合特征与辛普森悖论
一所美国高校的两个学院,分别是法学院和商学院。新学期招生,人们怀疑这两个学院有性别歧视。现作如下统计:
法学院
性别 录取 拒收 总数 录取比例
男生 8 45 53 15.1%
女生 51 101 152 33.6%
合计 59 146 205
商学院
性别 录取 拒收 总数 录取比例
男生 201 50 251 80.1%
女生 92 9 101 91.1%
合计 293 59 352
根据上面两个表格来看,女生在两个学院都被优先录取,即女生的录取比率较高。现在将两学院的数据汇总:
性别 录取 拒收 总数 录取比例
男生 209 95 304 68.8%
女生 143 110 253 56.5%
合计 352 205 557
在总评中,女生的录取比率反而比男生低。这个例子说明,简单的将分组数据相加汇总,是不能反映真实情况的。
将学院与性别组成[学院, 性别]二阶交叉特征,相比于将数据聚合后分析,可以丢失更少的信息。
Intuition behind Factorization
用户电影评分:

希望找到两个隐矩阵,他们相乘可以尽可能的接近打分矩阵


预测矩阵:

所以我们的目标就变成了找到P和Q使得偏差最小, 方法就是利用gradient descent使得以下的损失函数减到最小
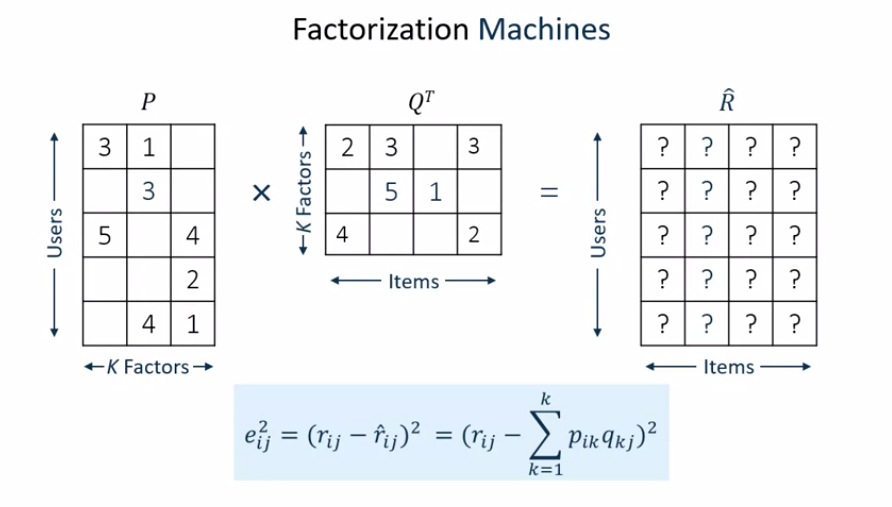
训练过后(O(kn)复杂度),用户电影喜好矩阵将被填满,这样就可以降序推荐给用户了。
recommendation example of user-movie:
https://zh.wikipedia.org/wiki/%E8%BE%9B%E6%99%AE%E6%A3%AE%E6%82%96%E8%AE%BA
https://www.analyticsvidhya.com/blog/2018/01/factorization-machines/
https://www.csie.ntu.edu.tw/~b97053/paper/Rendle2010FM.pdf
转载请注明出处: https://www.cnblogs.com/lnas01/p/13179336.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号