并查集基础版

并查集

（byd打到一半没保存直接关了乆乆乆）

并查集是一种数据结构，它可以用一个优秀的时间复杂度(路径压缩后接近\(O(1)\))来维持多个集合之间的关系，并进行查找和合并。

查找操作

我们可以定义一个并查集数组\(p[i]=j\)表示\(i\)的父亲（并查集实际是把一个一个的集合看做树来处理）是\(j\)。

初始化时令\(p[i]=i\)（这表示\(i\)为所在树的根）。

对于每一次查询\((i,j)\)是否在同一集合，我们可以递归的查找\(i,j\)两点所在树的根，如果根相同则表示\(i,j\)在同一集合内。

找根函数:

int root(int x){
	if(fr[x]==x)return x;
	return root(fr[x]);
}

合并操作

如何将\(x,y\)所在树合并呢？直接令p[x]=y可以吗？

不难发现，如果这样写会导致

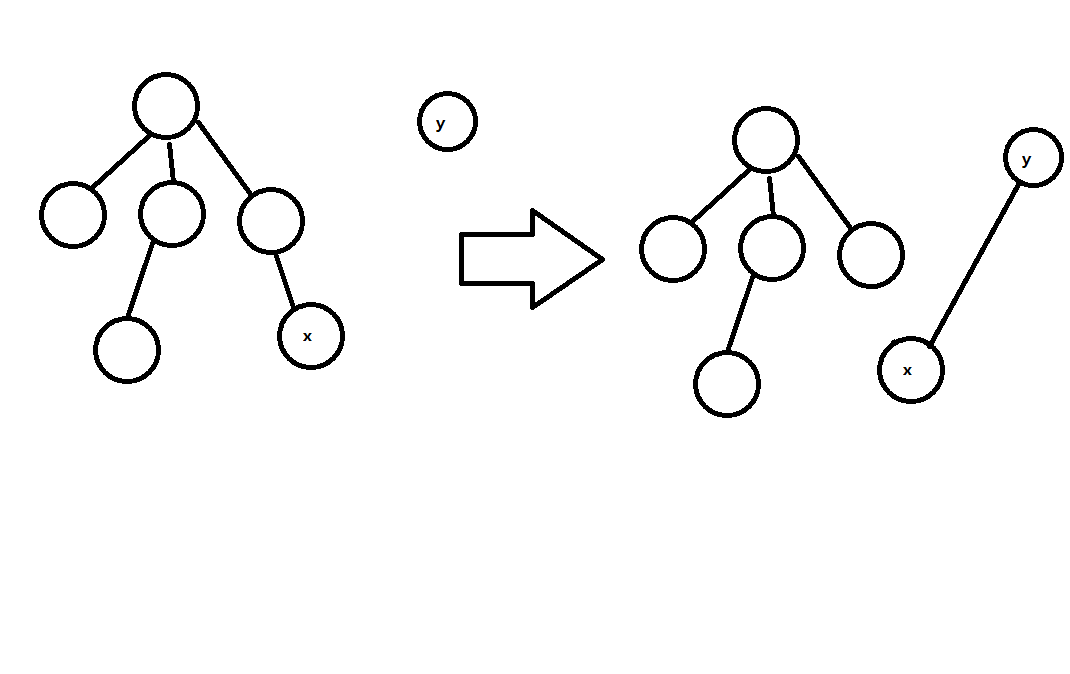
这就使得\(x\)与原集合之间的所属关系收到破坏。

解决方法是合并时令p[root(x)]=root(y)

画出图就是

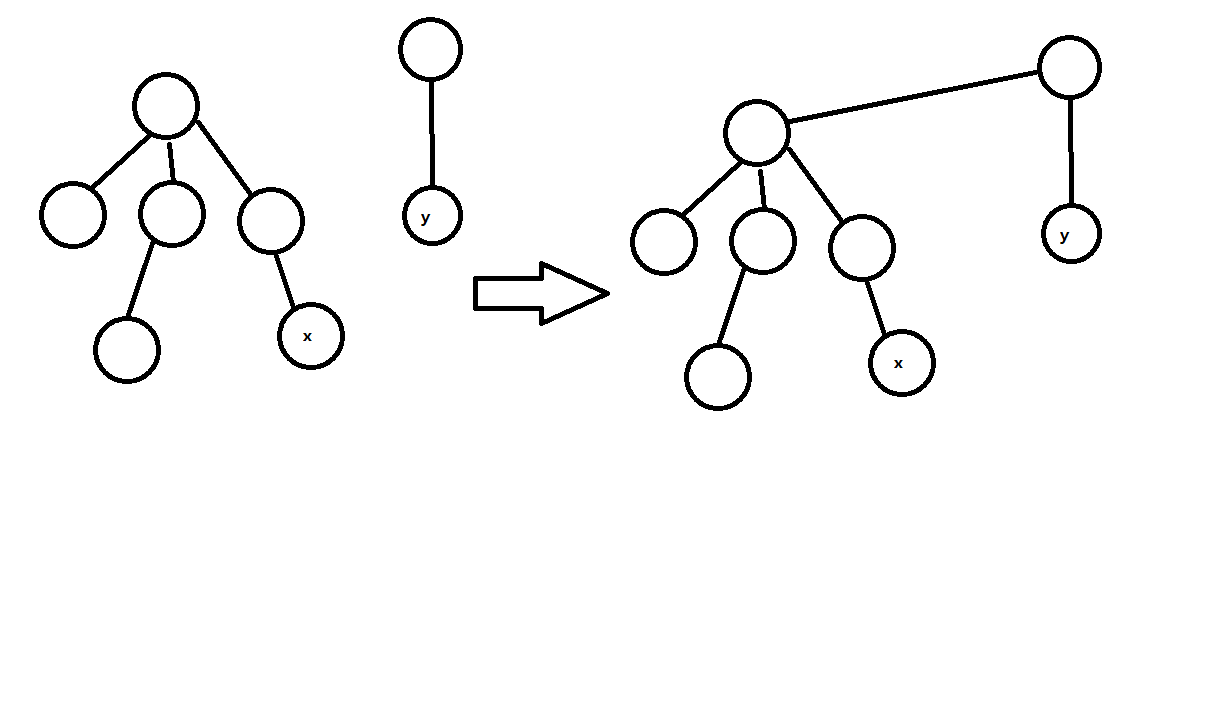
这样就完美解决了。

路径压缩优化。

让我们简单思考一下，这样写会有问题么？

假如洛谷模版题中有类似这样一组数据

10000 200000
1 1 2
1 2 3
1 3 4
1 4 5
...
...
...
...
1 10000 10001
2 10000 10001
2 10000 10001
...
...
...

让我们分析一下，按照之前的合并操作，这棵树最后会变成

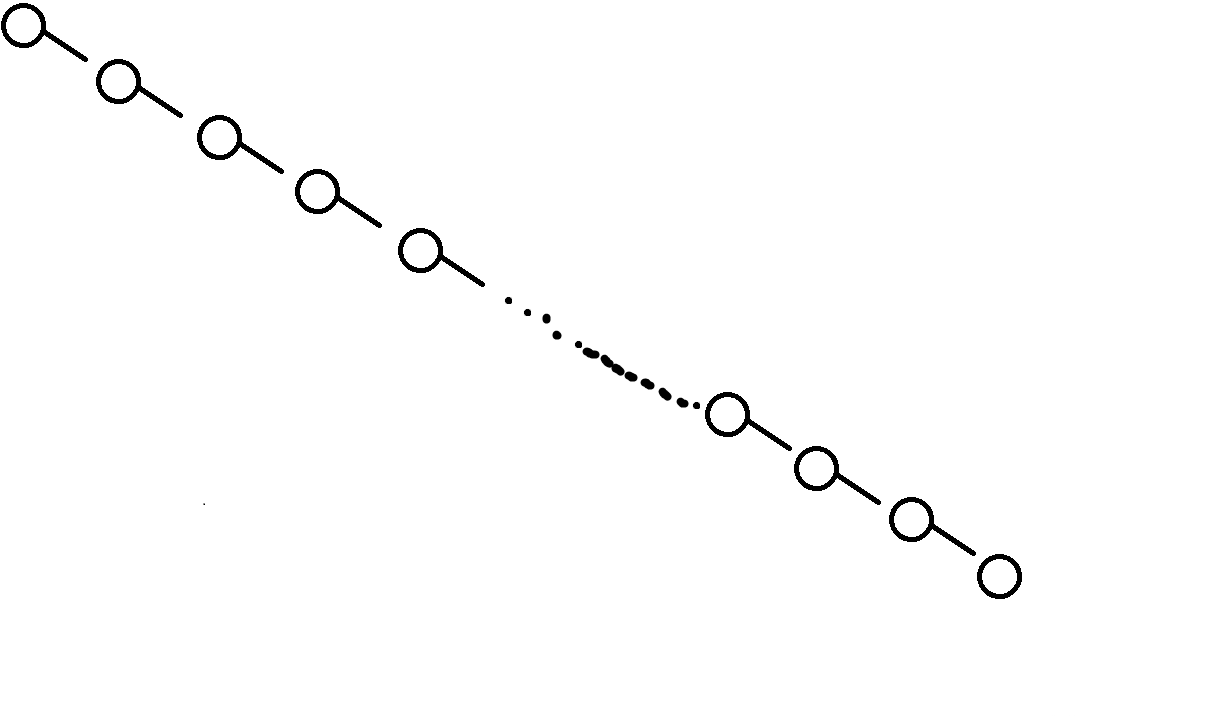
它退化成了一根链！在这种情况下，查询操作的复杂度就变成了\(O(n)\)。

\(10^5\)这种数量级的查找显然是遭不住的，那应该怎么优化呢？

这就要路径压缩了。我们先思考这样一个问题，查询操作的复杂度在什么时候最小呢？

显然，当树类似这样一个形状时

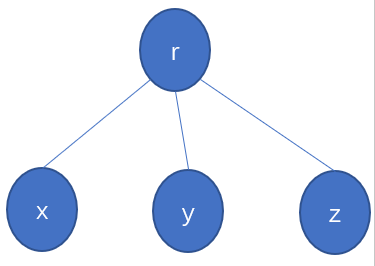
查询操作时间复杂度就变成了\(O(1)\)。

那应该如何实现呢？

不难发现，对于一棵树上的每一棵节点，他的位置并不重要，重要的是他的根是哪个点。所以，我们在查询的时候可以直接把这个点的父亲直接修改为根，由于是递归查询，如此一来他所在这一根枝条上的所有点都直接连在了根下面。

代码实现：

int root(int x){//并查集找根函数 
	if(f[x]==x)return x;
	return f[x]=root(f[x]);
}//“=”赋值也是有返回值的，返回值即为赋的值

基本并查集用法就这么多了，再往下就是进阶版本的并查集了orz