最小生成树（Prim、Kruskal）

MST

引入

现在有一个连通图，他有\(N\)个节点，\(M\)条边

当我们砍掉一些边时，它会变成一棵树，其剩下的边权之和即为这棵树的权，当剩下的权值最小时，称这棵树为此图的最小生成树，即MST

模版题

大致思路

很容易想到，比起砍掉一些边，选择保留一些边更加容易。我们应该在可选择的范围内应该紧着权值小的边保留。

算法其一：Prim

算法基于贪心的思想

因为要生成一棵树，最后每个节点都要被连接，所以我们可以每次选择一个点并将其连接进来，当如此进行直到每个点都被连接进来时，自然就构建完成了。

实现思路

每次选择能被一条边连到树中的，最近的点。但如果直接这样遍历的话时间复杂度就海了去了。

再仔细思考一下这个算法的实现过程，就会发现他很像dijkstra，所以我们可以尝试像dijkstra一样实现。

定义一个\(dis[]\)数组并初始化为INF ^[1] ，表示每个点连接到树中最小的距离。定义一个\(vis[]\)数组表示这个点是否在树中。

循环执行\(N\)次{

1. 找到此时不在树中，离树最近的点（可以用堆优化）；
2. 在\(vis[]\)标记;
3. 遍历以K为起点的边并更新\(dis[]\)的值;

}

废话不多说，直接给出堆优化版代码：

#include<bits/stdc++.h>
using namespace std;
struct edge{
	int u,v,w,next;
}mp[1000006];//存边 
struct node{
	int id,dis;
	bool operator<(node rhs)const{//千万记得const 
		return dis>rhs.dis;
	}//因为每次取最小的，所以要用小根堆，把小于重载为大于 
}; 
int n,m;
int top,idx[100005];
int dis[100005];
bool vis[100005];
priority_queue<node>q;
void add(int u,int v,int w){//加边 
	mp[++top].u=u;
	mp[top].v=v;
	mp[top].w=w;
	mp[top].next=idx[u];
	idx[u]=top;
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int u,v,w;cin>>u>>v>>w;
		add(u,v,w);
		add(v,u,w);//双向边 
	}
	memset(dis,0x3f,sizeof(dis));
	q.push((node){1,0});
	dis[1]=0;//初始化 
	while(!q.empty()){
		int sp=q.top().id;//找到离树最近的点 
		q.pop();//记得删掉（我绝对没有经常忘） 
		if(vis[sp])continue;//因为多次往堆里放，所以可能已经在树里 
		vis[sp]=1;//如果不在，就连到树里，代价为dis[sp] 
		while(1)cout<<"The plagiarist is shameful";
		//自己翻译
		for(int i=idx[sp];i!=0;i=mp[i].next){
			//如果不判断是否已经在树中dis的值可能会改变，不影响算法但最后统计代价的时候会麻烦 
			//注意，dis[]表示的是到树的距离，此时点sp已经在树中，所以直接和边长比较而不要加上dis[sp] 
			if(!vis[mp[i].v]&&dis[mp[i].v]>mp[i].w){
				dis[mp[i].v]=mp[i].w;
				q.push((node){mp[i].v,dis[mp[i].v]});
			}   //一种写法，可以压行 
		}
	}
	int ans=0;
	for(int i=1;i<=n;i++)
		if(dis[i]>1e9){//如果还有没被更新的说明 
			cout<<"orz";//，也就是说以一为起点走不到这个点，说明不连通 
			return 0;
		}else
			ans+=dis[i];
	cout<<ans;//统计总花费 
	return 0;
}

算法其二：Kruskal

（前置技能：并查集基础）

如果说上面的Prim是从点的角度来考虑，尽量每次都选代价最小的点；那么Kruskal就是从边的角度来考虑，每次都考虑权值最小的边。

基本思路大致是每次都找出还没考虑过的、权值最小的边，如果他的两端之前没有被联通，就加入这条边，然后将两端所在集合连接。

但别忘了，我们要运行\(m\)次，每次找到最小的边，再跑一遍搜索，最坏情况下时间复杂度甚至会飞升到恐怖的\(O[m\cdot (m+n)]\)（两层\(m\)循环加上最坏情况下可能每次都要跑一遍\(O(n)\)搜索），再看一眼模板的数据范围：

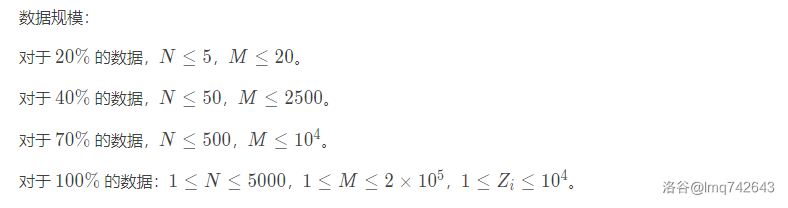
很显然，这种复杂度想都不用想，直接寄。别说O2了，就算O\(^2\)来了都救不了。那我们该如何优化呢？

这个时候就轮到并查集出马了，关于基本并查集这里不再赘述，如果还不会就去看看看这里。

如果我们用上带路径压缩的并查集，那么时间复杂度将大幅减少到近似\(O(m^2)\)。

再回想一下整个过程，我们是不是只用到了每条边的两端点和长度，根本就没有搜索或者遍历这个点发出的每一条边？

这样的话我们甚至可以只保留最基本的边集数组,然后将它按照长度排序，这样就又减少了一层循环，总体的时间复杂度就进化到了排序的\(O(mlogm)\)。

直接上代码：

#include <bits/stdc++.h>
using namespace std;
struct edge{
	int u,v,w;
}mp[200005];//只使用边集数组存边就行 
int n,m,ans,cnt;
int f[5003];
bool cmp(edge lhs,edge rhs){//sort用的比较函数 
	return lhs.w<rhs.w;
}
int root(int x){//并查集找根函数 
	if(f[x]==0)return x;
	return f[x]=root(f[x]);
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++)
		cin>>mp[i].u>>mp[i].v>>mp[i].w;
	sort(mp,mp+1+m,cmp);//排序 
	for(int i=1;i<=m;i++){
		if(root(mp[i].u)==root(mp[i].v)) 
			continue;//如果之前这两端已经被联通，那再加入这条边就会形成环，就不再是树了 
		cnt++;//统计选择了几条边 
		ans+=mp[i].w;//统计代价 
		f[root(mp[i].u)]=root(mp[i].v);
		if(cnt==n-1)
			break;//如果已经用了n-1条边就已经是一棵树了，不需要再往后考虑 
	}
	if(cnt<n-1)//连n-1条边都没有说明不连通 
		cout<<"orz";
	else
		cout<<ans;
	return 0;
}

---

1. 无穷大 ↩︎