堆排序
堆
堆(heap)是计算机科学中一类特殊的数据结构的统称，通常是一个可以被看做一棵树的数组对象。
堆{k1,k2,ki,…,kn} (ki <= k2i,ki <= k2i+1)|(ki >= k2i,ki >= k2i+1), (i = 1,2,3,4...n/2)
关于堆：
- 堆中某个节点的值总是不大于或不小于其父节点的值；
- 堆总是一棵完全二叉树（下面）。
- 将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。
完全二叉树
说到堆排序，就不能不提完全二叉树，这些基本概念在网上到处都是，我摘了个最简单的。。
完全二叉树：除最后一层外，每一层上的节点数均达到最大值；在最后一层上只缺少右边的若干结点。
我自己总结认为，正是因为有下面两个特点，
- 只允许最后一层有空缺结点且空缺在右边，即叶子结点只能在层次最大的两层上出现（存储方式的规则性）；
- 若i>1，tree的双亲为tree[i div 2]（其父子结点值的规律性）；
才使得其进行排序非常方便。
堆排序
堆排序求升序用大顶堆，求降序用小顶堆。
本例用求降序的小顶堆来解析。
堆排序步骤如下：
1、我们将数据（49、38、65、97、76、13、27、50）建立一个数组$arr；
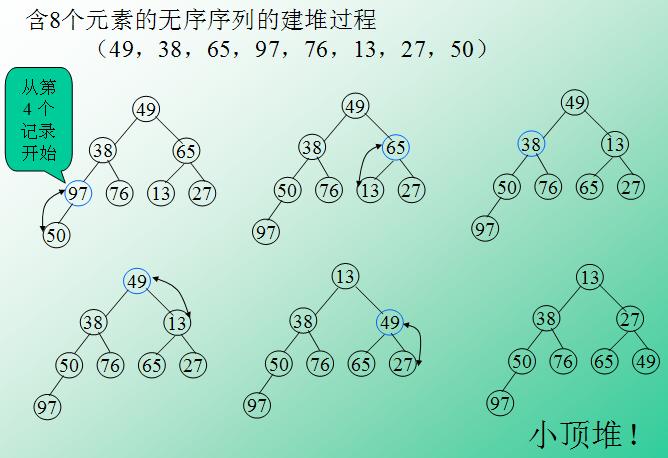
2、用数组$arr建立一个小顶堆（主要步骤，会在代码注释里解释，下图是用一个数组建立小顶堆的过程）；
3、将堆的根（最小的元素）与最后一个叶子交换，并将堆长度减一，跳到第二步；
4、重复2-3步，直到堆中只有一个结点，排序完成。
