CF div2 322 C

C. Developing Skills

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Petya loves computer games. Finally a game that he's been waiting for so long came out!

The main character of this game has n different skills, each of which is characterized by an integer a_i from 0 to 100. The higher the number a_i is, the higher is the i-th skill of the character. The total rating of the character is calculated as the sum of the values ​​of 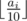for all i from 1 to n. The expression ⌊ x⌋ denotes the result of rounding the number x down to the nearest integer.

At the beginning of the game Petya got k improvement units as a bonus that he can use to increase the skills of his character and his total rating. One improvement unit can increase any skill of Petya's character by exactly one. For example, if a₄ = 46, after using one imporvement unit to this skill, it becomes equal to 47. A hero's skill cannot rise higher more than 100. Thus, it is permissible that some of the units will remain unused.

Your task is to determine the optimal way of using the improvement units so as to maximize the overall rating of the character. It is not necessary to use all the improvement units.

Input

The first line of the input contains two positive integers n and k (1 ≤ n ≤ 10⁵, 0 ≤ k ≤ 10⁷) — the number of skills of the character and the number of units of improvements at Petya's disposal.

The second line of the input contains a sequence of n integers a_i (0 ≤ a_i ≤ 100), where a_i characterizes the level of the i-th skill of the character.

Output

The first line of the output should contain a single non-negative integer — the maximum total rating of the character that Petya can get using k or less improvement units.

Sample test(s)

Input

2 4
7 9

Output

2

Input

3 8
17 15 19

Output

5

Input

2 2
99 100

Output

20

Note

In the first test case the optimal strategy is as follows. Petya has to improve the first skill to 10 by spending 3 improvement units, and the second skill to 10, by spending one improvement unit. Thus, Petya spends all his improvement units and the total rating of the character becomes equal to lfloor frac{100}{10} rfloor +  lfloor frac{100}{10} rfloor = 10 + 10 =  20.

In the second test the optimal strategy for Petya is to improve the first skill to 20 (by spending 3 improvement units) and to improve the third skill to 20 (in this case by spending 1 improvement units). Thus, Petya is left with 4 improvement units and he will be able to increase the second skill to 19 (which does not change the overall rating, so Petya does not necessarily have to do it). Therefore, the highest possible total rating in this example is .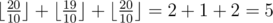

In the third test case the optimal strategy for Petya is to increase the first skill to 100 by spending 1 improvement unit. Thereafter, both skills of the character will be equal to 100, so Petya will not be able to spend the remaining improvement unit. So the answer is equal to .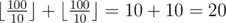

题意很清晰。。。可以用结构体排序做，我用的优先队列，然后模拟就行了

#include <cstdio>
#include <cstring>
#include <iostream>
#include <stack>
#include <queue>
#include <map>
#include <algorithm>
#include <vector>

using namespace std;

const int maxn = 1000005;

typedef long long LL;

vector<int>G[maxn];

priority_queue< pair<int,int> >Q;

int a[maxn];

int main()
{
    int n,m;
    int tmp = 0;
    int k;
    int ans = 0;
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++){
        scanf("%d",&tmp);
        ans += tmp/10;
        if(tmp < 100){
            int m = tmp / 10;
            int r = tmp % 10;
            Q.push(make_pair(r,m));
        }
    }
    bool flag = true;
    while(!Q.empty()&&k>0&&flag){
        int r = Q.top().first;
        int m = Q.top().second;
        Q.pop();
        flag = false;
        int re = 10 - r;
        if(k >= re){
            flag = true;
            k -= re;
            ans++;
            if(m < 9){
                Q.push(make_pair(0,m+1));
            }
        }
    }
    printf("%d\n",ans);
    return 0;
}