矩阵快速幂求fib
链接:https://www.nowcoder.com/acm/contest/189/D
来源:牛客网
题目描述
qn是个特别可爱的小哥哥,qy是个特别好的小姐姐,他们两个是一对好朋友 [ cp (划掉~)
又是一年嘤花烂漫时,小qn于是就邀请了qy去嘤花盛开的地方去玩。当qy和qn来到了田野里时,qy惊奇的发现,嘤花花瓣以肉眼可见的速度从树上长了出来。
仔细看看的话,花瓣实际上是以一定规律长出来的,而且,每次张成新的花瓣的时候,上一次的花瓣就会都落到地上,而且不会消失。
花瓣生长的规律是,当次数大于等于2时,第i次长出来的花瓣个数和上一次张出来的花瓣个数的差是斐波那契数列的第i-1项。初始的时候地上没有花瓣,树上的花瓣个数为1,第一次生长的花瓣个数为1。初始的那个花瓣就落到了地上
又是一年嘤花烂漫时,小qn于是就邀请了qy去嘤花盛开的地方去玩。当qy和qn来到了田野里时,qy惊奇的发现,嘤花花瓣以肉眼可见的速度从树上长了出来。
仔细看看的话,花瓣实际上是以一定规律长出来的,而且,每次张成新的花瓣的时候,上一次的花瓣就会都落到地上,而且不会消失。
花瓣生长的规律是,当次数大于等于2时,第i次长出来的花瓣个数和上一次张出来的花瓣个数的差是斐波那契数列的第i-1项。初始的时候地上没有花瓣,树上的花瓣个数为1,第一次生长的花瓣个数为1。初始的那个花瓣就落到了地上
现在,小qn想知道,经过k次生长之后,树上和地上的总花瓣个数是多少?
ps:斐波那契数列:
f[1]=f[2]=1;f[i]=f[i-1]+f[i-2] (i>=2且i  N+)
N+)
输入描述:
一行一个数k
输出描述:
一行一个数m,表示第k次生长过后,树上和地上的总花瓣数是多少。由于答案会很大,请你将答案mod 998244353后输出
备注:
对于0%的数据,有k=样例
对于20%的数据,有k<=1'000
对于60%的数据,有k<=1'000'000
对于80%的数据,有k<=1'000'000'000
对于100%的数据,有k<1'000'000'000'000'000'000
题解:本题是求fib的前n项和
这里有个结论,fib的前n项和=fib(n+2)-1
但是数据范围。。。。异常大,所以一看,只能矩阵快速幂加速递推了
先来讲一讲矩阵运算对于一个n*m的矩阵,只有m*p的矩阵才能与其进行乘法,最后乘出来是n*p
的矩阵,对于一个矩阵a,b
这道题用矩阵来写是这样的一个操作
首先我们设f(n)={f[n],f[n+1]},那么f(n-1)={f[n-1],f[n]}
那么矩阵f(n)的第一项等于矩阵f(n-1)的第二项,矩阵f(n)的第一项等于矩阵f(n-1)的第一项+第二项
实际上就等于所以,求f(n)就相当于求f(0)*
那么用快速幂处理
即可
代码:
#include<cstdio> #include<cstring> using namespace std; typedef long long ll; const ll mod=998244353; ll f[5]; ll c[5][5]={{0,0},{0,0,1},{0,1,1}}; void get(){ ll a[5]; memset(a,0,sizeof(a)); for (int i=1;i<=2;i++){ for (int k=1;k<=2;k++){ a[i]=(a[i]+f[k]*c[k][i]%mod)%mod; } } f[1]=a[1]; f[2]=a[2]; } void self(){ ll a[5][5]; memset(a,0,sizeof(a)); for (int i=1;i<=2;i++){ for (int j=1;j<=2;j++){ for (int k=1;k<=2;k++){ a[i][j]=(a[i][j]+c[i][k]*c[k][j]%mod)%mod; } } } for (int i=1;i<=2;i++) for (int j=1;j<=2;j++) c[i][j]=a[i][j]; } int main(){ f[1]=1; f[2]=1; ll k; scanf("%lld",&k); k+=2; for (;k;k>>=1){ if(k&1) get(); self(); } printf("%lld",f[1]-1); return 0; }


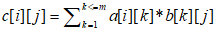

 浙公网安备 33010602011771号
浙公网安备 33010602011771号