tarjan算法与无向图连通性

一，无向图的割点与桥

对于G=(V,E)

   1.割点：xξV若删除x以及与x所连边后，图被分裂成为多个联通图，则x为图的割点

   2.桥（割边）：eξE若删除e后图，图被分裂成为多个联通图，则e为图的割点

 

怎样求割点与割边

tarjan算法

就是他了。。。

 

首先我们引入时间戳的概念

设dfsn[x]表示从源节点Y开始访问到的第几个

也就是说我们假设dfsn[Y]=1,然后我们采用深度优先搜索树对图进行访问

依次对图的访问次序进行标记

如图：

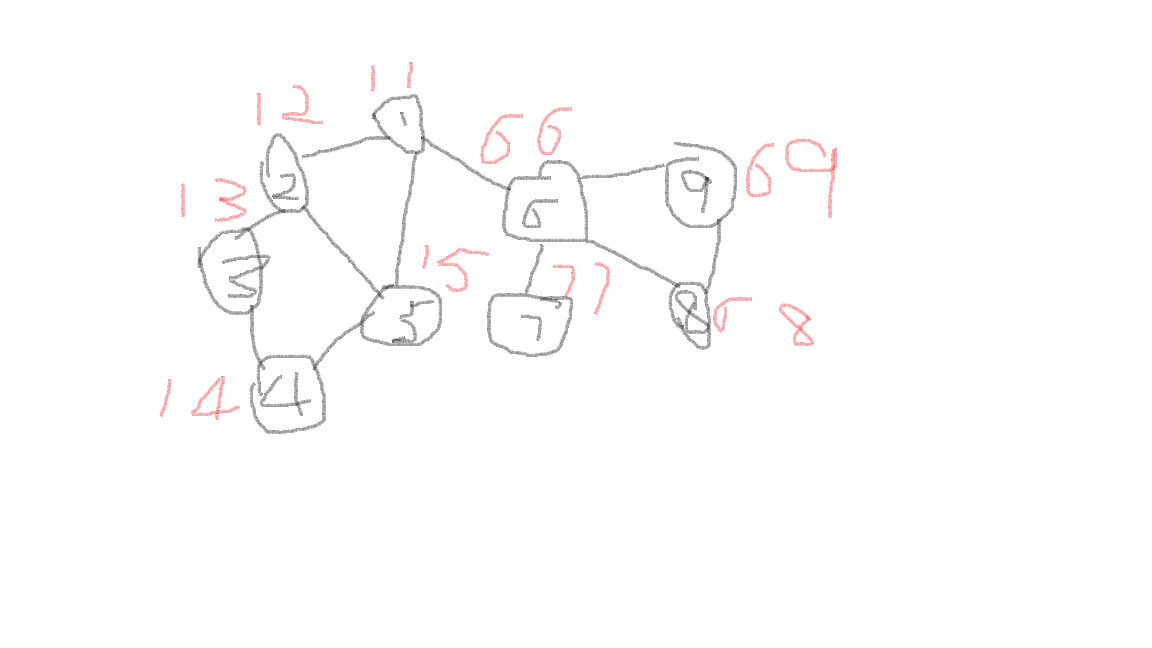
图中红色数字左表示low[x]值，右表示dfsn[x]值

什么是low[x]，值呢？

我们定义low[x]表示x通过它的子树所能到达的最早编号的节点的编号

如何更新low[x]值？

我们在dfs过程中，先让low[x]=dfsn[x]

有定义可知，设y为x子节点，则low[x]=min(low[x],low[y]);

如图，我们会发现节点5可以不通过它的父节点而到达节点1

所以,同样low[x]=min(low[x],dfsn[y])

怎样判断点是否为割点？

dfsn[x]<=low[y]

怎样判断边是否为割边？

dfsn[x]<low[y]

（x,y）为割边

割点代码

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

struct my{
  int next;
  int v;
};

const int maxn=100000;
int bridge[maxn<<1],dfsn[maxn],low[maxn];
int adj[maxn];
my bian[maxn<<1];
int fa=1,dfn;

void myinsert(int u,int v){
     bian[++fa].v=v;
     bian[fa].next=adj[u];
     adj[u]=fa;
}

void tarjan(int x,int x_bridge){
     low[x]=dfsn[x]=++dfn;
     for (int i=adj[x];i;i=bian[i].next){
        int v=bian[i].v;
        if(!dfsn[v]){
            tarjan(v,i);
            low[x]=min(low[x],low[v]);
            if(low[v]>dfsn[x]) {
                    bridge[i]=bridge[i^1]=true;

            }
        }
        else if(i!=(x_bridge^1)){
            low[x]=min(low[x],dfsn[v]);
        }
     }
}

int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    int u,v;
    for (int i=1;i<=m;i++) {
        scanf("%d%d",&u,&v);
        myinsert(u,v);
        myinsert(v,u);
    }
    for (int i=1;i<=n;i++){
            if(!dfsn[i])
            tarjan(i,1);
    }
    for (int i=2;i<fa;i+=2){
      if(bridge[i]) printf("%d %d\n",bian[i^1].v,bian[i].v);
    }
return 0;
}

 

#include<cstring>
#include<algorithm>
#include<cstdio>
using namespace std;

struct my{
   int v;
   int next;
};

const int maxn=100000;
int adj[maxn],cut[maxn],low[maxn],dfsn[maxn];
my bian[maxn];
int root,fa,dfn;

void myinsert(int u,int v){
     bian[++fa].v=v;
     bian[fa].next=adj[u];
     adj[u]=fa;
}

void tarjan(int x){
    dfsn[x]=low[x]=++dfn;
    int ch=0;
    for (int i=adj[x];i;i=bian[i].next){
        int v=bian[i].v;
        if(!dfsn[v]){
            tarjan(v);
            low[x]=min(low[x],low[v]);
            if(low[v]>=dfsn[x]){
                ch++;
                if(x!=root||ch>1){
                    cut[x]=true;
                }
            }
        }
        else low[x]=min(low[x],dfsn[v]);
    }
}

int main(){
    int n,m;
    int u,v;
    scanf("%d%d",&n,&m);
    for (int i=1;i<=m;i++){
        scanf("%d %d",&u,&v);
        myinsert(u,v);
        myinsert(v,u);
    }
    for (int i=1;i<=n;i++){
        if(!dfsn[i]) {
                root=i;
                tarjan(i);
        }
    }
    for (int i=1;i<=n;i++) if(cut[i]) printf("%d\n",i);
return 0;
}