线段树
线段树主要用于动态修改某个/区间的值,求某个/区间的和,区间最大/小值,等等跟区间有关的都可以尝试用线段树
线段树的操作都是在lgn内完成的
例如:输入n<1e5,然后输入n个数,q次询问,每次询问先输入opt,
如果opt=1,接下来输入l,r,v,代表l~r区间的数都加上v
如果opt=2,接下来输入l,r,让你输出l到r位置的数字的和是多少
如果暴力需要n2,但是线段树可以实现为nlgn
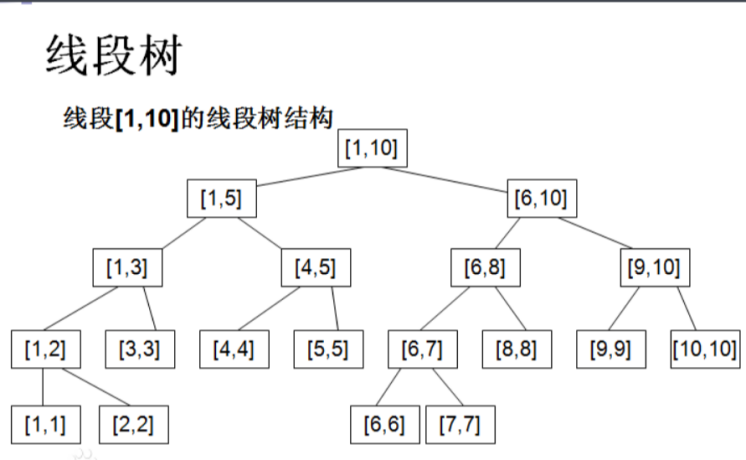
线段树主要就建了一个二叉树,每个点都存储一个区间的值,然后每个节点有两个子节点(除了区间大小是1的),一半一半的存储本节点的区间值,所以每一层(最后一层可能会有差的)都能不重不漏的存储整个1~n的值
由于每次都是一半一半分割,因此树的高度就是lgn了,那么查询任何一个点都可以在lgn内找到那个点
对于任何一个区间,都可以由不到2*lgn的节点表示(因为区间连续,而且要不重不漏,所以不存在父子节点和兄弟节点同时标记,那么相当于每层最多只有两个)
一般来说数组都是开成正常数组的4倍,空间是够得
其中a[i]数组代表第i个位置的值是多少
f[i]数组代表,第所指向的区间的值之和(有时候可以改成最大值,最小值,看需求是什么了)
yc[i]数组用于延迟,当yc[i]不是0的时候,代表子区间的值需要更新,那么当要用到子区间的时候,就顺便更新即可。
函数rt是节点在f数组中下标,ls,rs是本节点左孩子节点和右孩子节点在数组中的下标,
L,R代表这个节点所管辖的区间,l,r是要操作的区间,
#include<stdio.h> #define rep(i,j,k) for(int i=j;i<=k;++i) #define ls rt<<1 #define rs rt<<1|1 #define N 4*100005 int a[N],f[N],yc[N]; void build(int rt,int L,int R) { yc[rt]=0; if(L==R) { f[rt]=a[L];///记录这个区间的和,只有一个点时,就是这个点的值 return ; } int mid=(L+R)/2;///每次都分成一半 build(ls,L,mid); build(rs,mid+1,R); f[rt]=f[ls]+f[rs]; } void up(int rt,int L,int mid,int R)///用来把延迟标记去掉,更新f数组 { if(yc[rt])///代表需要更新 { f[ls]+=yc[rt]*(mid-L+1); f[rs]+=yc[rt]*(R-mid); yc[ls]+=yc[rt]; yc[rs]+=yc[rt]; yc[rt]=0; } } void update(int rt,int L,int R,int l,int r,int v) { if(l<=L&&R<=r)///因为这个区间是修改的子区间,所以加个延迟标记,以后要更新子区间的时候直接一起更新就好 { f[rt]+=v*(R-L+1);///虽然有延迟标记,但是延迟标记只能记录他的所有子区间,本个区间的f要一直更新好 yc[rt]+=v; return ; } int mid=(L+R)/2; up(rt,L,mid,R);///去掉延迟 if(l<=mid)///代表左孩子的区间中含有更新的区间 update(ls,L,mid,l,r,v); if(r>=mid+1)///代表右孩子的区间中含有更新的区间 update(rs,mid+1,R,l,r,v); f[rt]=f[ls]+f[rs]; } int query(int rt,int L,int R,int l,int r) { if(l<=L&&R<=r) return f[rt]; int mid=(L+R)/2,ans=0; up(rt,L,mid,R);///去掉延迟 if(l<=mid)///代表左孩子的区间中含有查询的区间 ans+=query(ls,L,mid,l,r); if(r>=mid+1)///代表右孩子的区间中含有查询的区间 ans+=query(rs,mid+1,R,l,r); return ans; } int main() { int n; scanf("%d",&n); rep(i,1,n) scanf("%d",&a[i]); build(1,1,n); int q; scanf("%d",&q); int l,r,v; while(q--) { int opt; scanf("%d",&opt); if(opt==1) { scanf("%d %d %d",&l,&r,&v); update(1,1,n,l,r,v); } else { scanf("%d %d",&l,&r); printf("%d\n",query(1,1,n,l,r)); } } }




