DS博客作业02--线性表
0.PTA得分截图

1.本周学习总结
1.1 总结线性表内容
- 线性表:线性表是最基本、最简单、也是最常用的一种数据结构。线性表是数据结构的一种,一个线性表是n个具有相同特性的数据元素的有限序列。
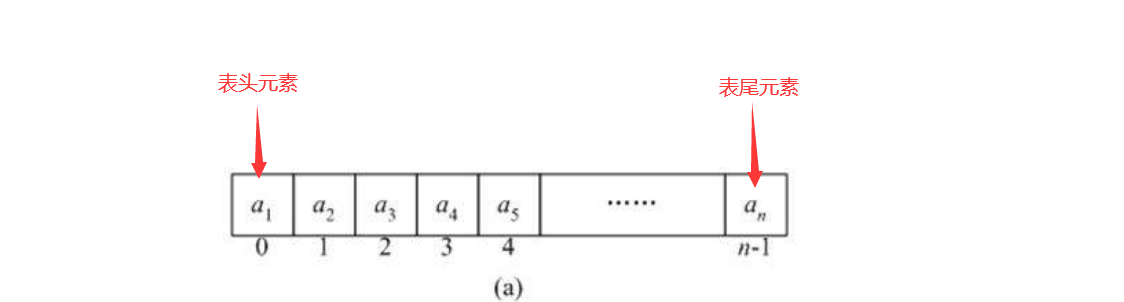
- 线性表中数据元素的关系是一对一的,(大部分)线性表除了第一个和最后一个元素以外,所有元素都是相互链接在一起的。(循环链表除外,循环链表尾指针指向头元素)
- 一般选择使用线性表的原因是它逻辑结构简单,便于实现和操作。
(线性与非线性只是逻辑层次上讨论,即使双向链表和循环链表与一般的线性表有所不同但是它们仍属于线性表)
1.1.1顺序表结构体定义
typedef int ElemType;
typedef struct
{
ElemType data[MaxSize]; //存放顺序表元素
int length ; //存放顺序表的长度
} List;
typedef List *SqList;
- 此类顺序表结构定义实际上是在栈区申请空间,即用的是数组,这种方法简便容易理解,这也是我们常用的方法,但是这种方法有一点不足就是栈区申请的空间是有限的,若数组很大时,则这种方法就行不通。
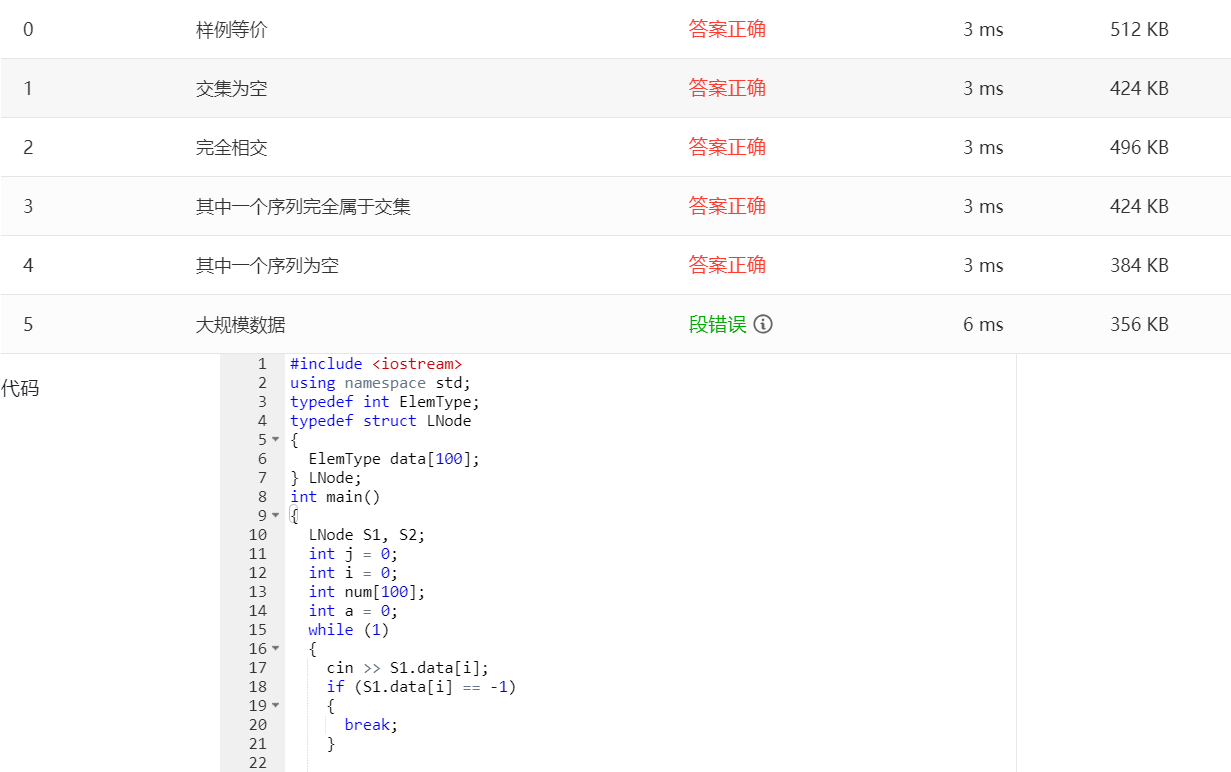
正如这道题,我用了这种栈区申请的做法,并把数组的大小定义为100,那么最后一个测试点大规模数据就无法通过,即使将数组的容量扩大也是无济于事。因此,我们不得不想过另一种方法来实现这段代码。
也就是我接下来要说的第二种顺序表结构定义的方法
typedef int ElemType;
typedef struct
{
ElemType *data; //存放顺序表元素
int length ; //存放顺序表的长度
} List;
typedef List *SqList;
- 这种方法就是在堆区申请空间,使用这种方法的好处是:堆区是动态申请的,我们需要多少内存空间可以自己申请,即利用mollac,new函数,这块空间不受限制
- 其实两种方法相差不打,更多的是看个人使用的习惯,但是这边建议还是主要利用第二种方法养成习惯。
1.1.2顺序表插入
InsertSq(SqList *&L,int x):顺序表L中插入数据x
void InsertSq(SqList& L, int x)
{
int i = 0;
L->data[L->length] = 1000;
while (L->data[i] <= x)
{
i++;
}
if (i == L->length)
{
L->data[L->length] = x;
return;
}
int j = L->length-1;
for (j; j >=i; j--)
{
L->data[j + 1] = L->data[j];
}
L->data[i] = x;
}
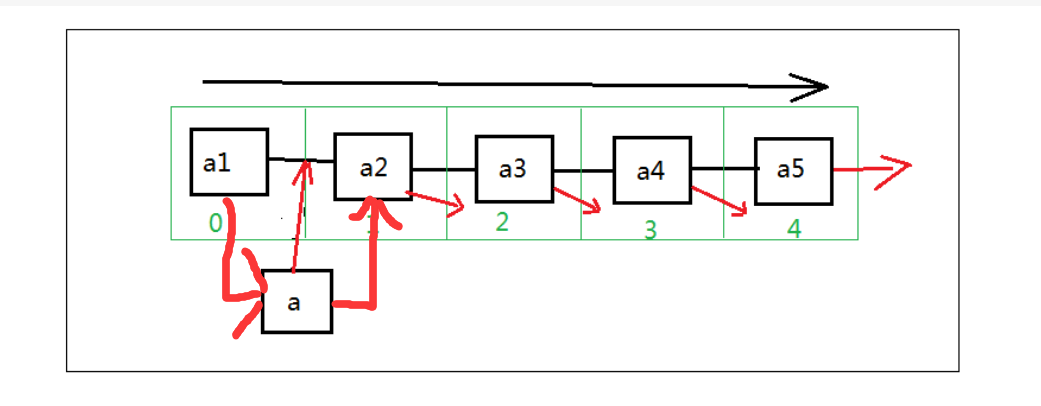
插入做法
1.找插入位置
2.数组元素a[i]--a[n]后移一个位置
3.a[i]插入数,表长度加一
- 其实对线性表的基本操作只需要理解透彻了,代码顺序其实也就记住了,原则就是不能破坏线性表的线性结构,即:插入或者删除元素是不能使线性表在中途断裂,也就是失去和后继元素的联系,只要在保持了联系的前提下,对线性表完成操作,那么就几乎不会出现错误。
1.1.3顺序表删除
以PTA上一题删除重复数据的题目为例
void DelSameNode(List& L)
{
int count=0;
for (int i = 0; i < L->length; i++)
{
for (int j = i + 1; j < L->length; j++)
{
if (L->data[i] == L->data[j])
{
for (int m = j; m < L->length; m++)
{
L->data[m] = L->data[m + 1];
}
L->length--;
j--;
}
}
}
L->length = L->length ;
}
顺序表删除
1.找删除位置
2.将要删除的元素后的元素向前移动一个位置
3.数组长度减一

1.1.3链表结构体定义
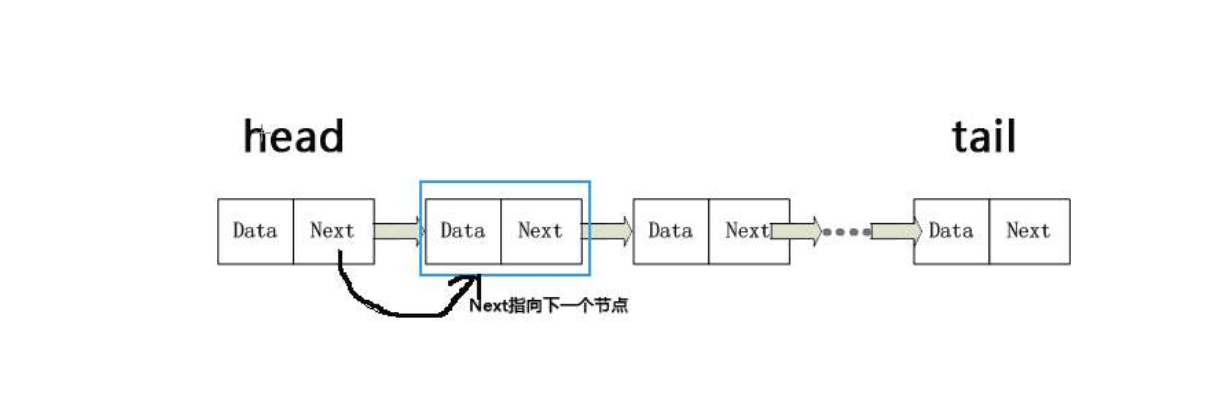
链表不同于顺序表,链表各数据之间是没有逻辑联系的,即是一种非连续,非顺序的储存结构。
- 对链表进行插入操作时,比顺序表的插入操作更为简便,但是链表查找元素的效率确实大大不如顺序表的,使用链表可以克服数组链需要事先知道数组元素的数据大小的弊端,链表结构可以充分利用计算机的内存空间,形成灵活的动态处理
typedef struct LNode //定义单链表结点类型
{
ElemType data;
struct LNode *next; //指向后继结点
} LNode,*LinkList;
1.1.4头插法

代码实现如下:
void CreateListF(LinkList& L, int n)
{
LinkList pre;
L = new LNode;
L->next = NULL;
for (int i = 0; i < n; i++)
{
pre = new LNode;
cin >> pre->data;
pre->next = L->next;
L->next = pre;
}
}
- 头插法的实质其实就是输出元素和输入元素的顺序相反,很多情况下可以巧妙的利用头插法来解决问题
例如:以此题单链表逆置为例
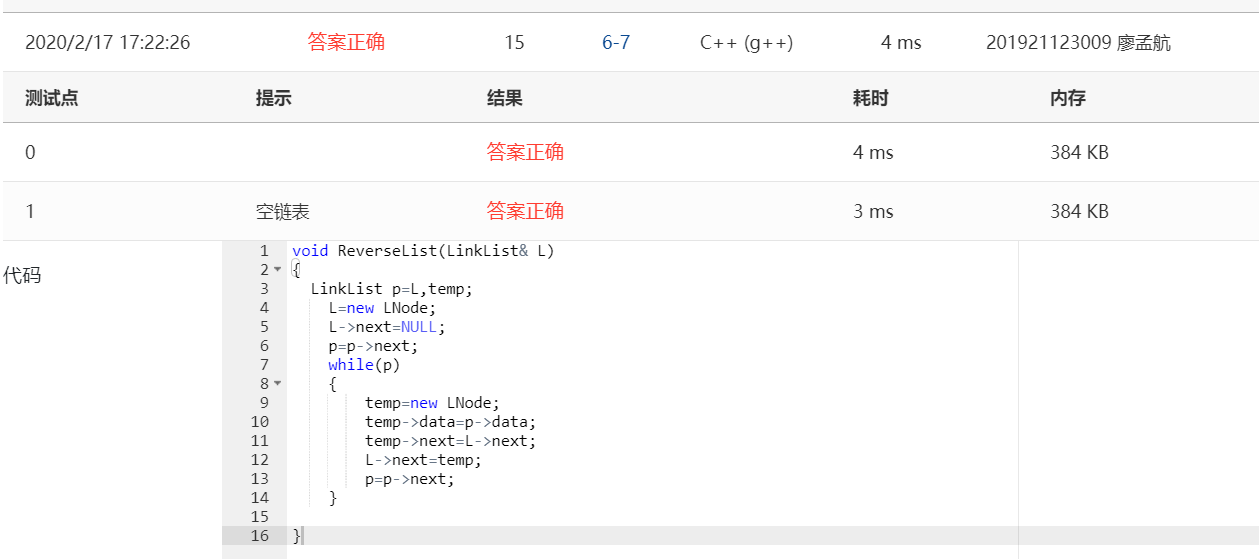
这就是将头插法灵活应用的结果
1.1.5尾插法
尾插法代码实现如下:
void CreateListR(LinkList& L, int n)
{
LinkList ptr,end;
L = new LNode;
end = L;
for (int i = 0; i < n; i++)
{
ptr = new LNode;
cin >> ptr->data;
end->next = ptr;
end = ptr;
}
}
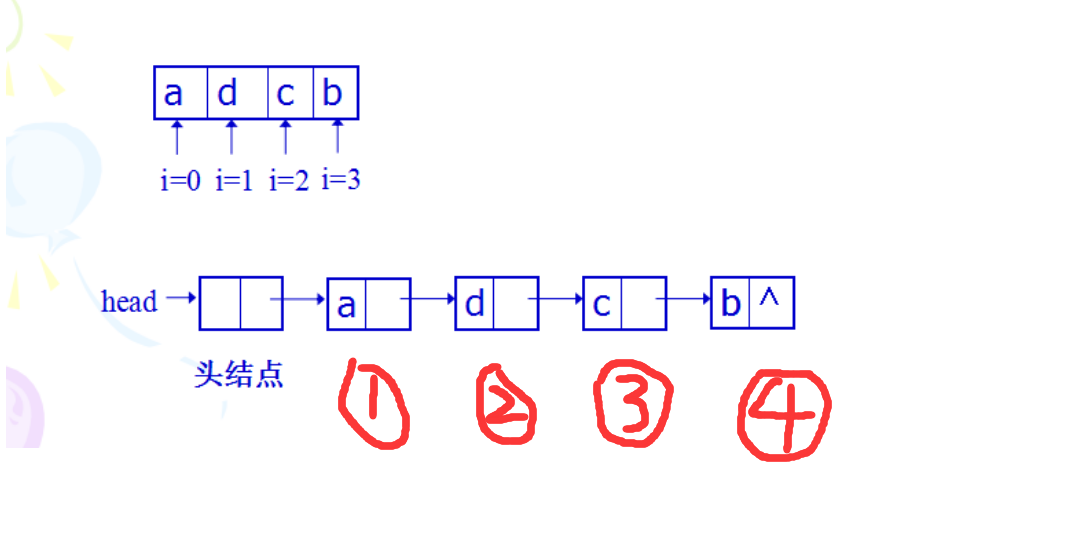
- 尾插法输出结果顺序即为输入顺序,也是较为常见的方法
1.1.6链表插入与删除
- 链表的插入与删除操作相对于顺序表来说较为简便,顺序表进行这类操作是需要对数组挪动,这就导致了其时间复杂度较大,而链表的插入与删除只需要在插入位置改动指针的前驱和后继就可以达到目的
即,改动数据的前后联系

代码实现如下
void ListInsert(LinkList& L, ElemType e)//有序链表插入e元素
{
LinkList p = L, q;
q = new LNode;
int flag=0;
q->data = e;
q->next = NULL;
while (p->next)
{
if (p->next->data >= e)
{
q->next = p->next;
p->next = q;
flag=1;
break;
}
p = p->next;
}
if (flag == 0)p->next = q;
}
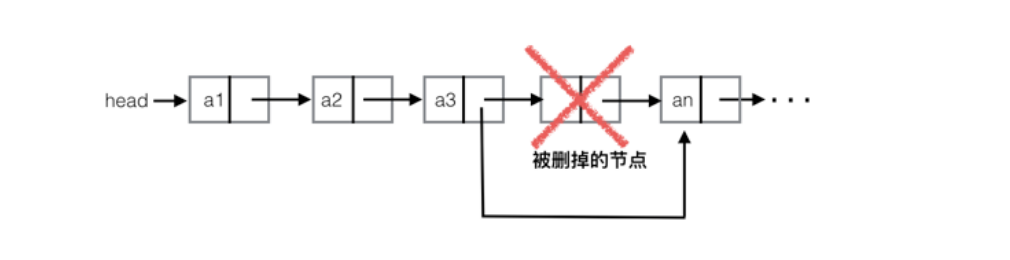
有序链表删除代码实现
void ListDelete(LinkList& L, ElemType e)//删除e元素
{
int flag=0;
LinkList p = L, q;
if (p->next == NULL)return;
while (p->next)
{
if (p->next->data == e)
{
p->next = p->next->next;
flag=1;
break;
}
p = p->next;
}
if (flag == 0)cout << e << "找不到!" <<endl;
}
1.1.7有序表合并
- 首先进行有序表的合并,在接收输入数据时并建链表时就应该对数据进行从大到小的排序,在这里我认为有序表的合并有两种方法,其各有各的好处
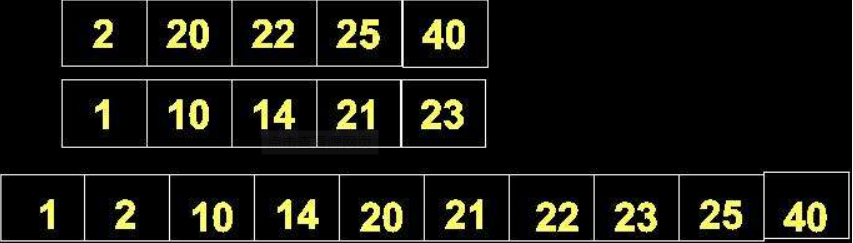
第一种也是较为常见的一种
bool merge(struct SqList* LL1,struct SqList* LL2,struct SqList* LL3)
{
if((LL1->length+LL2->length)>LL3->length)
return false;
int i=0;
int j=0;
int k=0;
while((i<LL1->length)&&(j<LL2->length))
{
if(LL1->data[i]<=LL2->data[j])
{
LL3->data[k]=LL1->data[i];
i++;
k++;
}
else
{
LL3->data[k]=LL2->data[j];
j++;
k++;
}
}
while(i<LL1->length)
{
LL3->data[k++]=LL1->data[i++];
}
while(j<LL2->length)
{
LL3->data[k++]=LL2->data[j++];
}
LL3->length=k;
return true;
}
- 这种方法大概就是把两条链的元素关系都断开只保留其头节点,再对所有元素对比排序,其实相当于就是将所有元素重新放入一个新链表,这种方法简单易懂,且操作难度不大,
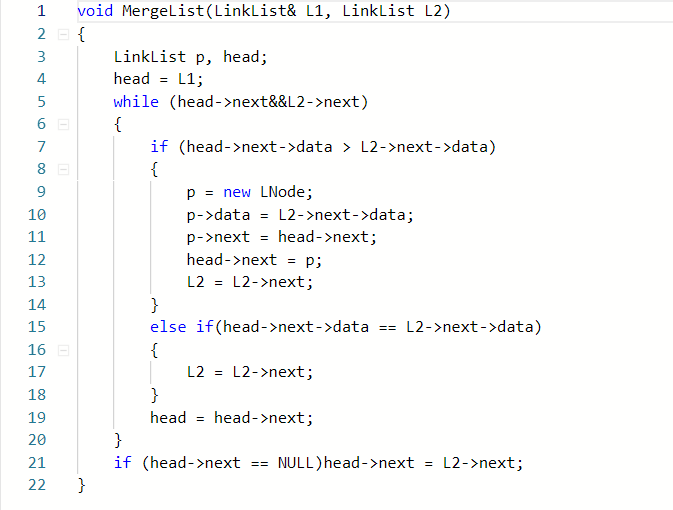
第二种方法
void MergeList(LinkList& L1, LinkList L2)
{
LinkList p, head;
head = L1;
while (head->next&&L2->next)
{
if (head->next->data > L2->next->data)
{
p = new LNode;
p->data = L2->next->data;
p->next = head->next;
head->next = p;
L2 = L2->next;
}
else if(head->next->data == L2->next->data)
{
L2 = L2->next;
}
head = head->next;
}
if (head->next == NULL)head->next = L2->next;
}
- 两种方法的原理差不多,但第二钟方法保留了其中一条链,只分解了第二条链,通过数据的对比,将第二条链的数据插入进第一条链中。这种方法的好处就是能够使需要讨论的情况减少,使代码更为简洁,比如在结尾处第一种方法还需要判断两钟情况,即:第一条链更长,和第二条链更长的情况,而第二种方法由于我们是将一条链的基础上进行操作,若是该链是较长的那一条链,这种情况就可以不用讨论了,只需讨论另一条链更长的情况,节省了代码量
1.1.8循环链表、双链表结构特点
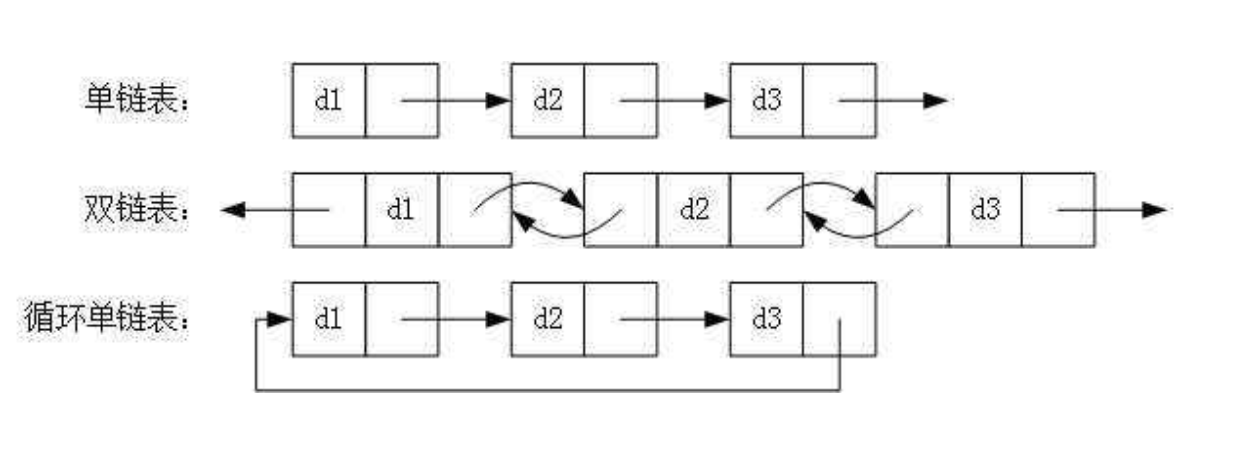
循环链表是另一种形式的链式存贮结构。它的特点是表中最后一个结点的指针域指向头结点,整个链表形成一个环
判断空链表的条件是
head==head->next;
rear==rear->next;
循环链表的建立
Node *CreateLoopLinkList(int n){
Node *p;
Node *tail;//指向尾结点的指针
LinkList=new Node;
LinkList->next=NULL;
head=LinkList;
for(auto i=0;i<n;i++){
p=new Node;
p->data=i;
LinkList->next=p;
LinkList=p;
}
//将尾结点赋值给尾指针
tail=LinkList;
//将尾指针的指针域指向头结点指向的指针域
tail->next=head->next;
return head;
}
1.循环链表的优点是无须增加存储量,仅对表的链接方式稍作改变,即可使得表处理更加方便灵活
2.循环链表中没有NULL指针。涉及遍历操作时,其终止条件就不再是像非循环链表那样判别p或p->next是否为空,而是判别它们是否等于某一指定指针,如头指针或尾指针等
3.在单链表中,从一已知结点出发,只能访问到该结点及其后续结点,无法找到该结点之前的其它结点。而在单循环链表中,从任一结点出发都可访问到表中所有结点,这一优点使某些运算在单循环链表上易于实现。
- 双向链表也叫双链表,是链表的一种,它的每个数据结点中都有两个指针,分别指向直接后继和直接前驱。所以,从双向链表中的任意一个结点开始,都可以很方便地访问它的前驱结点和后继结点。一般我们都构造双向循环链表。
定义双向链表
typedef struct Node
{
int data;
struct Node *pNext;
struct Node *pPre;
}NODE, *pNODE;
创建双向链表
pNODE CreateDbLinkList(void)
{
int i, length = 0, data = 0;
pNODE pTail = NULL, p_new = NULL;
pNODE pHead = (pNODE)malloc(sizeof(NODE));
if (NULL == pHead)
{
printf("内存分配失败!\n");
exit(EXIT_FAILURE);
}
pHead->data = 0;
pHead->pPre = NULL;
pHead->pNext = NULL;
pTail = pHead;
printf("请输入想要创建链表的长度:");
scanf("%d", &length);
for (i=1; i<length+1; i++)
{
p_new = (pNODE)malloc(sizeof(NODE));
if (NULL == p_new)
{
printf("内存分配失败!\n");
exit(EXIT_FAILURE);
}
printf("请输入第%d个元素的值:", i);
scanf("%d", &data);
p_new->data = data;
p_new->pNext = NULL;
p_new->pPre = pTail;
pTail->pNext = p_new;
pTail = p_new;
}
return pHead;
}
- 双向链表的优点:删除单链表中的某个结点时,一定要得到待删除结点的前驱,得到该前驱有两种方法,第一种方法是在定位待删除结点的同时一路保存当前结点的前驱。第二种方法是在定位到待删除结点之后,重新从单链表表头开始来定位前驱。尽管通常会采用方法一。但其实这两种方法的效率是一样的,指针的总的移动操作都会有2*i次。而如果用双向链表,则不需要定位前驱结点。因此指针总的移动操作为i次。
1.2.谈谈你对线性表的认识及学习体会。

- 数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关。都说数据结构在我们学习的现阶段来说是一个承上启下的作用,而线性表又是其中重要的一环,其实在上学期末,老师就已经让我们接触了链表,当然,刚开始学还是把上学期的知识忘得差不多了。我认为数据结构是一个操作性实用性非常强的,包括我们之后要学的栈、队列、排序、优先队列等等,都事可以广泛的应用的生活中的。计算机专业本科生都开设数据结构课程,它是计算机学科知识结构的核心和技术体系的基石。研究生考试也是必考科目,在这么多种储存方式中,判断方法,储存方法都是各不相同,可以说代码也是非常多种,有的时候能听到抱怨声,说数据结构中许多操作背不下来,这当然不是死记硬背的,记住每种不同储存结构的储存方式
- C语言中参数的传递分为值传递和指针传递,而C++中多了一个引用传递。值传递和指针传递都不可以改变传递进来的值,但指针可以改变其所指向的值。在C语言中,调用函数时传入的参数叫做“实参”,而在函数声明或定义中在函数头中的参数叫做“形参”。值传递与指针传递中,形参的改变是不影响实参的。C++中,引用传递,形参与实参实际上是同一个内容的不同名字,因而形参的变化会改变实参。引用传递是C++中一个很重要也很方便的特性,比如在可能会产生不必要的复制时,采用引用传递是一个很不错的解决方案。
2.PTA实验作业
2.1.题目1:jmu-ds-链表分割
2.1.1
2.1.2本题PTA提交列表说明。

- 一开始的部分正确是我用了另一种方法,看到题目是分割链表,而且需要一个头插法一个尾插法,那我就想先把简单的先将链表奇数位先输出,利用flag记录奇偶。再将剩下的偶数链的数字储存在一个数组中,再用头插法再次建链,但是这种方法第二个测试点过不去,我也找不到原因
- 第二次尝试我就换了一个方式,就相当于利用一个循环和flag让奇数偶数位的链分别做不一样的事,这样的思路我觉得是完全没问题的,但是这次变得更错了
- 在vs里调试后发现,按照这种方法来做的话实际上尾插法的那条连是要多做一次操作的这样,我就利用了一个oldc来使一下操作只进行一次,然后再进行正常操作,问题就解决了
if (oldc == 1)
{
q = new LNode;
q->data = head->data;
L2->next = q;
continue;
}
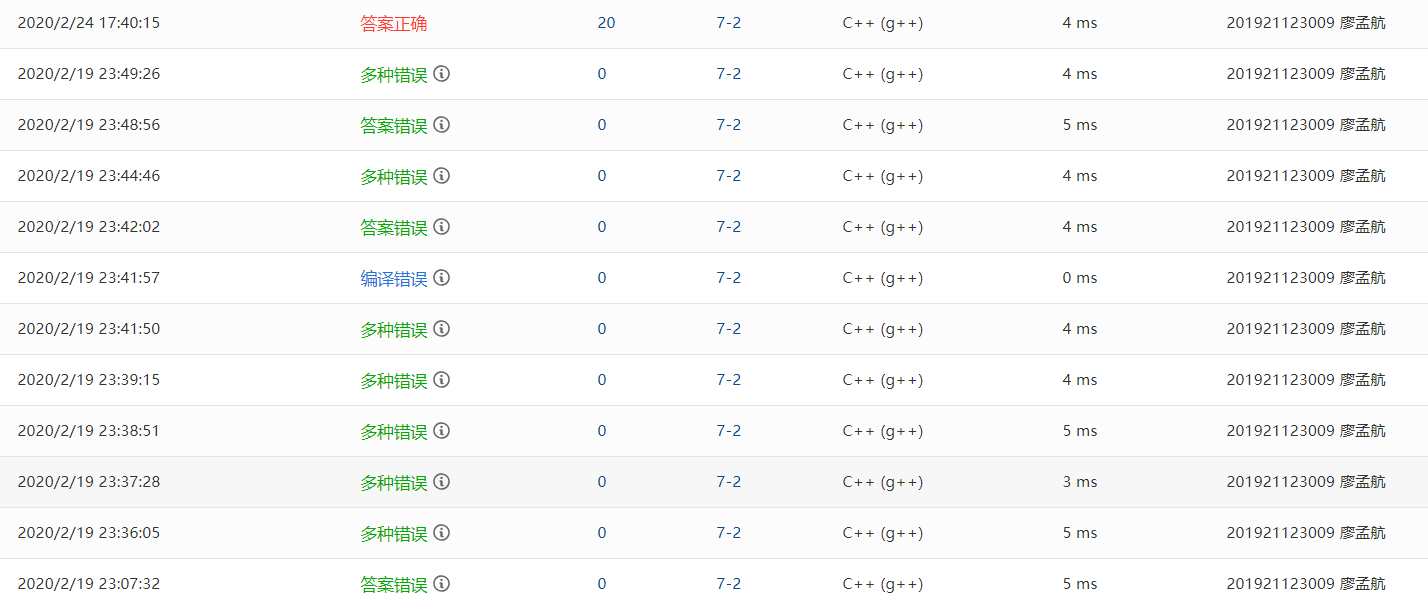
2.2 7-2 一元多项式的乘法与加法运算
正确代码如下


2.1.2本题PTA提交列表说明。
其实把这题放在这我主要是有些疑问,因为这题是多项式相加相乘,其实最主要的就是结构体中的指数位,再利用数组的一些操作其实不难写出,但是这题最后还是参考同学的代码才正确的
因为这题我花了非常多的时间,不是这题很难,是因为我调试感觉答案没问题,但是pta上不让过,格式的问题我也考虑过,但是还是找不出问题所在
我一开始代码如下:
#include<iostream>
#include<string>
using namespace std;
typedef int ElemType;
typedef struct LNode
{
ElemType p;
ElemType q;
struct LNode* next;
}LNode, * LinkList;
int main()
{
LinkList L1, L2, head1, head2, m, n;
int num1, num2;
L1 = new LNode;
L2 = new LNode;
cin >> num1;
head1 = L1;
head2 = L2;
for (int i = 0; i < num1; i++)
{
m = new LNode;
cin >> m->p;
cin >> m->q;
head1->next = m;
head1 = head1->next;
}
head1->next = NULL;
cin >> num2;
for (int i = 0; i < num2; i++)
{
n = new LNode;
cin >> n->p;
cin >> n->q;
head2->next = n;
head2 = head2->next;
}
head2->next = NULL;
head1 = L1->next;
head2 = L2->next;
LinkList max1, max2, data;
max1 = head1;
max2 = head2;
int number;
int a1[100], b1[100], a2[100], b2[100];
for (int i = 0; i < num1; i++)
{
a1[i] = max1->q;
a2[i] = max1->p;
max1 = max1->next;
}
for (int i = 0; i < num2; i++)
{
b1[i] = max2->q;
b2[i] = max2->p;
max2 = max2->next;
}
int c[100], d[100];
int u = 0;
for (int i = 0; i < num2; i++)
{
for (int j = 0; j < num1; j++)
{
c[u] = a2[j] * b2[i];
d[u] = a1[j] + b1[i];
u++;
}
}
int count = 0;
for (int i = 0; i < u; i++)
{
for (int m = i + 1; m < u; m++)
{
if (d[i] == d[m])
{
c[i] = c[i] + c[m];
count++;
for (int j = m; j < u; j++)
{
c[j] = c[j + 1];
}
for (int j = m; j < u; j++)
{
d[j] = d[j + 1];
}
}
}
}
for (int i = 0; i < u - count; i++)
{
cout << c[i] << " ";
cout << d[i];
if (i <= u - count - 2)
{
cout << " ";
}
}
cout << endl;
for (int i = 0; i < num1; i++)
{
for (int j = 0; j < num1; j++)
{
if (j >= num2 && i >= num1)
{
exit(0);
}
if (j >= num2 && i < num1)
{
cout << a2[i] << " ";
cout << a1[i];
if (i <= num1)
{
cout << " ";
}
i++;
continue;
}
if (i >= num1 && j < num2)
{
cout << b2[j] << " ";
cout << b1[j];
if (i < num1 || j < num2)
{
cout << " ";
}
continue;
}
if (a1[i] > b1[j])
{
cout << a2[i] << " ";
cout << a1[i];
if (i < num1 || j < num2)
{
cout << " ";
}
i++;
j--;
continue;
}
if (a1[i] == b1[j])
{
cout << a2[i] + b2[j] << " ";
cout << a1[i];
if (i < num1 || j < num2)
{
cout << " ";
}
i++;
continue;
}
if (a1[i] < b1[j])
{
cout << b2[j] << " ";
cout << b1[j];
if (i < num1 || j < num2)
{
cout << " ";
}
continue;
}
}
}
}
2.3 7-1 jmu-ds-有序链表合并
2.1.3本题PTA提交列表说明。
- 我一开始设置的循环是,把两条链不停的往下走,但是如果遇到两条链的值相等的情况下,数据需要保存,如若按照没改过的代码就可能会出现,循环输出几位数字
- 还有一个问题就是没有注意到合并后要删除重复数字
3.阅读代码
3.1 删除链表的倒数第N个节点(leetcode 19)
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n){
ListNode* right = head;
ListNode* left = head;
for (int i = 0; i < n; i++) {
right = right->next;
}
if (right == nullptr) {
head = head->next;
return head;
}
while (right->next != nullptr) {
left = left->next;
right = right->next;
}
left->next = left->next->next;
return head;
}
};
3.1.1 该题的设计思路
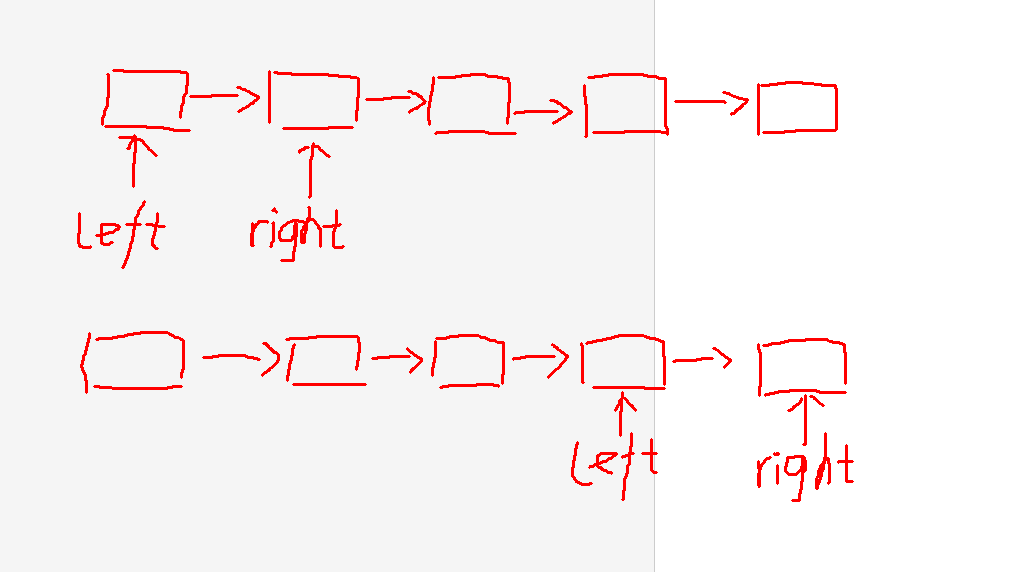
该题利用两个指针,以一种不同的方式解决了问题
给定一个链表: 1->2->3->4->5, 和 n = 2.
当删除了倒数第二个节点后,链表变为 1->2->3->5.
时间复杂度位O(n),空间复杂度为O(1)
3.1.2 该题的伪代码
ListNode* removeNthFromEnd(ListNode* head, int num) {
将right,left的值分别等于head
for (移动指针right) {
到达需要删的正序位置
}
if 若超出链表范围,退出
while (right->next != nullptr) {
left与right指针向下移动
}
删除元素
return head;
}
3.1.3 运行结果
3.1.4分析该题目解题优势及难点。
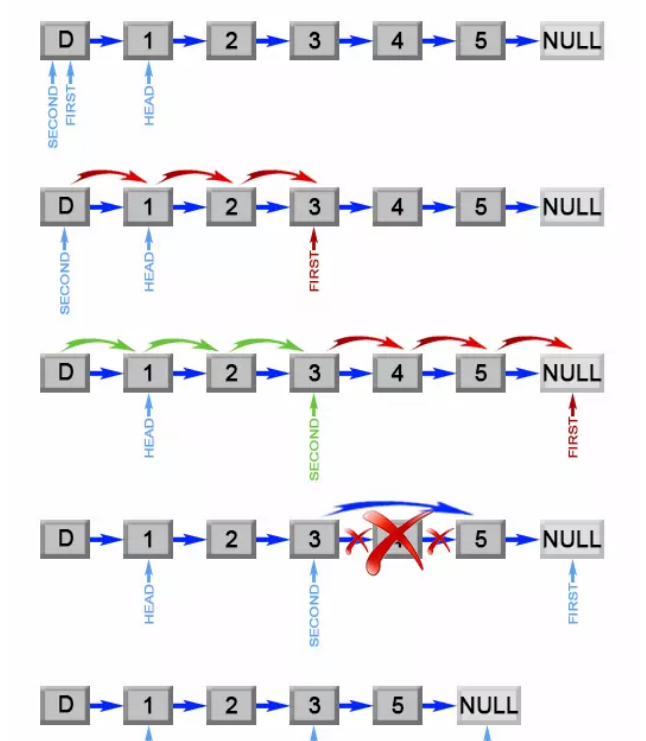
该题亮点即为运用了双指针法,使本题只需遍历一次链表就能找出需要删除的元素,降低了时间复杂度
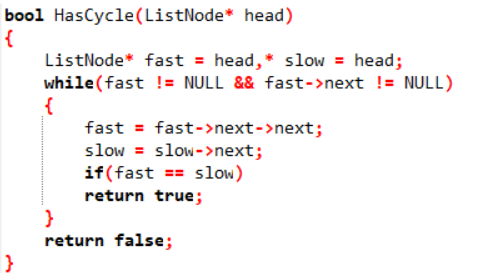
3.1 判断一个单链表中是否有环
3.1.1 该题的设计思路
如果一个链表中有环,也就是说用一个指针去遍历,是永远走不到头的。因此,我们可以用两个指针去遍历,一个指针一次走两步,一个指针一次走一步,如果有环,两个指针肯定会在环中相遇。时间复杂度为O(n)
3.1.2 该题的伪代码
定义两个快,慢指针fast,slow;
while(fast != NULL && fast->next != NULL)
{
slow往后移一位;
fast往后移2位;
if (fast==slow)//即为两者相遇
return true;
}
end while
return false;
3.1.3 运行结果
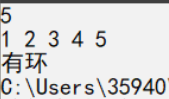
3.1.4分析该题目解题优势及难点。
- 运用了快慢指针,方法新颖,很好的利用了环状链表的特性,即指针遍历无法到头
- 且要注意建链表时注意把头尾指针连起来即tail->=head不要漏了


