SIFT特征学习笔记

SIFT(Scale Invariant Feature Transform)，尺度空间不变特征，目前手工设计的最好vision特征。

以下是学习http://blog.csdn.net/zddblog/article/details/7521424后的收获。

一、尺度空间

gaussian pyramid的产生：

1、为避免对第一组第一层图片（原始图片）做高斯滤波导致损失，在其基础上将尺度扩大一倍作为-1层，方法是用=0.5做高斯滤波。

2、对每组（octave）倒数第三张图片做降采样，产生下组的第一层图片（第一组不用），由于降采样，越往上图片越小。

3、每层图片在上一层基础上做高斯滤波。

所谓尺度即一张图片的精细程度或概括度，用度量，

由下往上尺度变大。尺度用高斯函数中的方差来描述。

从2.1的高斯分布图可知，对一个区域做高斯滤波，若方差越大（峰越低），则这个点被平滑得越厉害，那么图像就变得越模糊。在模糊的图片中我们看到的是更宏观的东西（大，尺度大），而清晰的图片看到的是更为微观的东西（小，尺度小）。

点->线，边缘，角点->轮廓形状->鼻子，嘴巴->头->人（尺度由小到大）

组（O，octave），层（S），尺度（）三者的关系：

可见逐组逐层递增。

二、尺度空间上的关键点选取

关键点，即金字塔上的三维局部极值点。（三维：x，y，，每张图上的位置及图的尺度）

1、首先对gaussian做高斯差分（Difference of Gaussian，DOG）

即上层减下层。

原因：2002年Mikolajczyk在详细的实验比较中发现尺度归一化的高斯拉普拉斯函数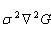的极大值和极小值同其它的特征提取函数，例如：梯度，Hessian或Harris角特征比较，能够产生最稳定的图像特征。而Lindeberg早在1994年就发现高斯差分函数（Difference of Gaussian ，简称DOG算子）与尺度归一化的高斯拉普拉斯函数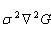非常近似。