归并排序

原地归并的抽象方法。

实现归并排序的一个直截了当的方法是将两个不同的有序数组归并到第三个数组中（他们都实现了Comparable接口）。但是当数组很大时要进行多次归并，因此在每次归并时都创立数组会带来性能问题。如果有一种能原地归并的方法，这样先将左半部分排序，再将右半部分排序，然后再数组中移动元素。乍一看很简单，实际上所有的实现都非常复制。实际上，将原地归并抽象化仍然很有帮助。

相关代码：

   private static Comparable[] aux;
    private static boolean less(Comparable<Object> a,Comparable<Object> b)
    {
        return a.compareTo(b)<0;
    }
    public static void merge(Comparable[] a,int start,int mid,int end )
    { 
        int i=start;
        int j=mid+1;
        for(int k=start;k<=end;k++)
        {
            aux[k]=a[k];
        }
        
        for(int k=start;k<=end;k++)
        {
            if(i>mid) a[k]=aux[j++];
            //左边用尽取右边
            else if(j>end) a[k]=aux[i++];
            //右边用尽取左边
            else if(less(aux[i],aux[j])) a[k]=aux[i++];
            //左边比右边小取左边
            else a[k]=aux[j++];
            //左边比右边大取右边
            
        }
    }

 

 

 

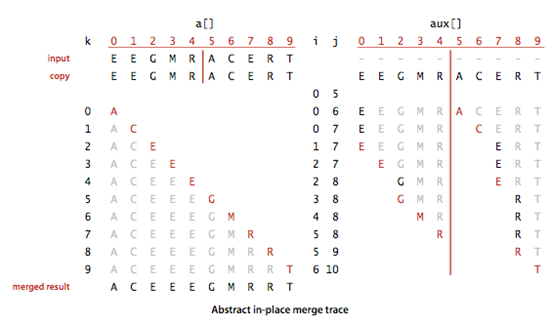
算法轨迹

自顶向下的归并排序

 

public class Main {
    private static Comparable[] aux;
    private static boolean less(Comparable<Object> a,Comparable<Object> b)
    {
        return a.compareTo(b)<0;
    }
    public static void merge(Comparable[] a,int start,int mid,int end )
    { 
        int i=start;
        int j=mid+1;
        for(int k=start;k<=end;k++)
        {
            aux[k]=a[k];
        }
        
        for(int k=start;k<=end;k++)
        {
            if(i>mid) a[k]=aux[j++];
            //左边用尽取右边
            else if(j>end) a[k]=aux[i++];
            //右边用尽取左边
            else if(less(aux[i],aux[j])) a[k]=aux[i++];
            //左边比右边小取左边
            else a[k]=aux[j++];
            //左边比右边大取右边
            
        }
    }
    
    public static void sort(Comparable[] a)
    {
        aux=new Comparable[a.length];
        sort(a,0,a.length-1);
    }
    private static void sort(Comparable[] a,int start,int end)
    {   if(end<=start) return;
        int mid=start+(end-start)/2;
        sort(a,start,mid);
        sort(a,mid+1,end);
        merge(a,start,mid,end);
        
    }
}

算法轨迹

   sort(a,0,15)

将左半部分排序：

      sort(a,0,7)

          sort(a,0,3)

            sort(a,0,1)

              merge(a,0,0,1)

            sort(a,2,3)

              merge(a,2,2,3)

            merge(a,0,1,3)

          sort(a,4,7)

            sort(a,4,5)

              merge(a,4,4,5)

            sort(a,6,7)

              merge(a,6,6,7)

            merge(a,4,5,7)

         merge(a,0,3,7)

将右半部分排序：

      sort(a,8,15)

          sort(a,8,11)

            sort(a,8,9)

              merge(a,8,8,9)

            sort(a10,11)

              merge(a,10,10,11)

            merge(a,8,9,11)

          sort(a,12,15)

            sort(a,12,13)

              merge(a,12,12,13)

            sort(a,14,15)

              merge(a,14,14,15)

            merge(a,12,13,15)

         merge(a,8,11,15)

归并结果：

   merge(a,0,7,15);

我们也可以采用树的形式简单描述：

 

 

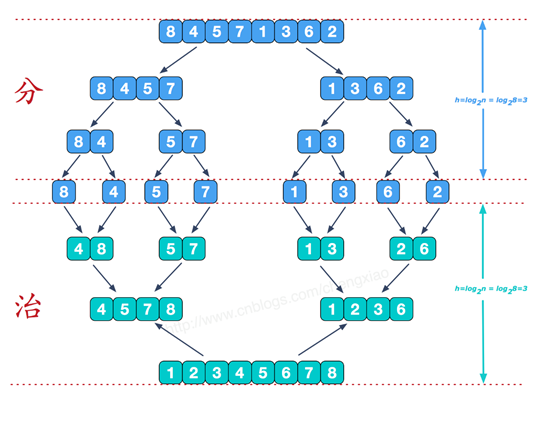
改进思路：

我们直到递归会使小规模的问题中的方法调用非常频繁，当要排序的数组很小时，我们可以选择采用插入排序或选择排序的方法

 

自底向上归并排序：

我们先归并那些微型数组，然后再成对归并得到的子数组，如此这般，直到将整个数组归并在一起。首先我们进行两两归并（把每个元素当成大小为一的数组），然后四四归并（将两个大小为2的数组归并为一个含有4个元素的数组），以此类推，最后一次归并的第二个数组可能比第一个小，但这并不是问题。

代码实现：

public static void sort0(Comparable[] a)
    {
        int N=a.length;
        aux=new Comparable[N];
        for(int sz=1;sz<N;sz=sz+sz)
          for(int start=0;start<N-sz;start+=sz+sz)
          {
              merge(a,start,start+sz-1,Math.min(start+sz+sz-1, N-1));
          }
    }

 

 

上面的是数组大小恰好为sz的偶数倍的情况，现在我们看一下一个例子：

0 7

1 6

2 5

3 4

4 3

5 2

6 1

现在一共有七个元素，0到6为下标，红色为下标对应的元素。现在来看排序轨迹（从小到大排）：

当sz=1时，两两归并

此时

0 6	1 7	2 4	3 5	4 2	5 3	6 1
归并 Start=0,end=start+sz+sz-1=1		归并 Start=0+sz+sz=sz=2,end=start+sz+sz-1=3		归并 Start=0+sz+sz=sz=4,end=start+sz+sz-1=5		归并

对于下标为6的那个元素，因为start=4+sz+sz=6,end=start+sz+sz-1=7,end越界，只能取N-1（N为元素个数）这就是为什么需要用到Math.min(start+sz+sz-1,N-1)的原因，此时的merge为merge(a,start,start+sz-1, Math.min(start+sz+sz-1,N-1))

即merge(a,6,6,6)

当sz=2时：

 

0 4	1 5	2 6	3 7	4 1	5 2	6 3
归并 Start=0,end=start+sz+sz-1=3				归并 Start=0+sz+sz=sz=4,end=start+sz+sz-1=7 越界

对于右边的归并，end越界，所以取N-1，此时merge为

merge(a,4,5,6)

以此类推，排序完毕

 

算法分析：

子数组的大小sz初始值为1，每次增加一倍，最后一个子数组的大小自有在数组大小是sz的偶数倍的时候才会等于sz，否则只会小于sz.,例如，现在要排序的数组有16个元素，

当我们要进行十六十六归并的时候，每个子数组大小为8，16正好为8的偶数倍，所以此时可以进行十六十六归并，但如果只有15个元素，15不是8的偶数倍，所以此时不能进行十六十六归并，最后一个子数组大小为7，我们就将这个子数组直接合并到已经排序的数组中。start+sz+sz-1如果小于N-1说明我们仍然能进行（2*sz）(2*sz)的归并。

当数组的长度为2的幂时，两种归并排序的比较次数和数组访问次数正好相等，只是顺序不同，自底向上的归并排序比较适合与链表组织的数据，想象将链表先当成1的子链表排序，然后是大小为2的子链表，以此类推，这种方法只需要重新组织链表链接就能原地排序，不需要创建任何新的链表节点