前言:从图中的任一顶点出发,对图中的所有顶点访问一次且只访问一次称为图的遍历。
深度优先遍历
走迷宫:
为了更好的理解深度优先遍历,我们先来考虑一下一个经典的问题——走迷宫。
我们使用Tremaux搜索。
- 在身后放一个绳子
- 访问到的每一个地方放一个绳索标记访问到的交会点和通道
- 当遇到已经访问过的地方,沿着绳索回退到之前没有访问过的地

代码实现:

1 public class DepthFirstSearch { 2 3 private boolean[] marked; 4 private int count; 5 6 public DepthFirstSearch(Graph G,int S) 7 { 8 marked=new boolean[G.V()]; 9 10 } 11 12 private void dfs(Graph G,int V) 13 { 14 marked[V]=true; 15 count++; 16 for(int w:G.adj(V)) 17 { 18 if(!marked[w]) 19 dfs(G,w); 20 } 21 } 22 public boolean marked(int w) 23 { 24 return marked[w]; 25 } 26 27 public int count() 28 { 29 return count; 30 } 31 32 33 }
深度优先遍历就是用一个递归的方法访问一个顶点,在访问其中一个顶点时,只要
(1):将它标记为已经访问;
(2):递归的访问它所有没有被标记过的邻居节点。
跟踪算法的行为:
为了方便描述,我们假设迷宫是由单项通道构成的,在碰到边v-w时,要么递归的进行调用(w没有被访问),要么跳过(w已经被标记)。当再从w-v遇到这条边的时候,总会忽略它,因为另一端V已经访问过了。跟踪图示如下:
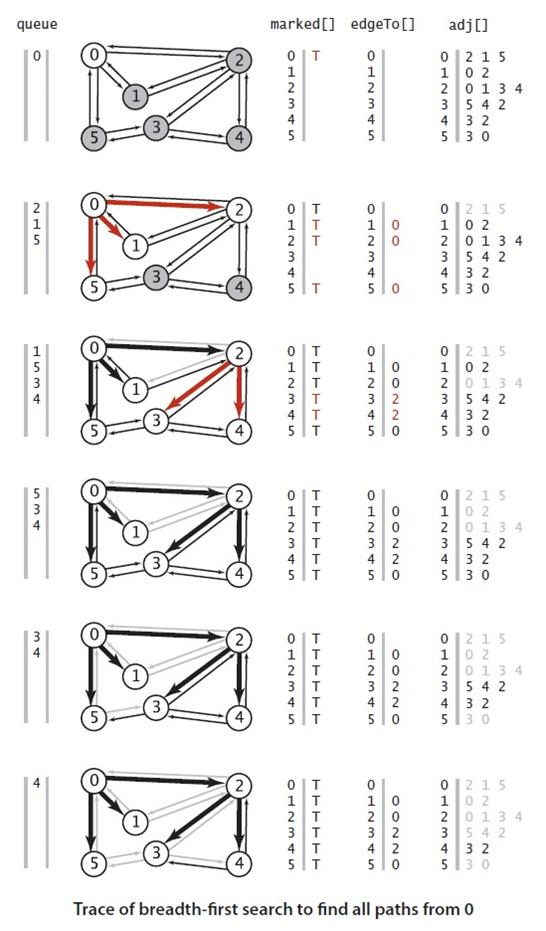
现在来分析这张图:
起点为0,查找开始于构造函数调用dfs来标记和访问顶点0,
(1): 因为2是0的邻接表的第一个元素且没有被访问过,dfs()递归调用自己来访问顶点2,(实际上系统将顶点0和0的邻接表的当前位置压入栈中)。
(2):顶点0是2的第一个元素但是已经被标记过了,dfs会跳过它,1是2的第二个元素且没有被标记过,dfs()递归调用自己来访问顶点1.(系统将顶点2和2的邻接表的当前位置压入栈中)
(3)对于顶点1,因为它的邻接表的所有顶点均已被访问过,方法从dfs(1)返回,接下来检查2-3,(2的邻接表中1后面是3),dfs()递归调用自己来访问顶点3.
(4)因为5是3的邻接表的第一个元素且没有被访问过,dfs()递归调用自己来访问顶点5.
(5),5的邻接表的所有顶点都已经被标记,不需要在递归。
(6)、因为4是3的邻接表的第二个元素且没有被访问过,dfs()递归调用自己来访问顶点4.
(7)、此时实际上已经遍历完。dfs()不断检查(实际上是出栈),发现所有顶点均标记。
总结:实际上深度优先遍历就是一个不断进栈出栈的过程,对于上面的图遍历,访问某一个顶点,实际上就是将此元素入栈,而元素出栈的条件就是他的邻接表中的所有元素都被标记(访问过)。
利用深度优先遍历,我们可以判断两个顶点之间是否连通:
我们定义以下API:

我们需要定义一个变量来记录已经找的路径。
代码实现:

1 public class DepthFirstPaths { 2 3 private boolean[] marked; 4 private int s; 5 private int[] edgeTo; 6 public DepthFirstPaths(Graph G,int S) 7 { 8 marked=new boolean[G.V()]; 9 edgeTo=new int[G.V()]; 10 this.s=S; 11 dfs(G,S); 12 } 13 14 private void dfs(Graph G,int V) 15 { 16 marked[V]=true; 17 18 for(int w:G.adj(V)) 19 { 20 if(!marked[w]) 21 edgeTo[w]=V; 22 dfs(G,w); 23 } 24 } 25 public boolean hasPathTo(int w) 26 { 27 return marked[w]; 28 } 29 30 public Iterable<Integer> pathTo(int v) 31 { 32 if(!hasPathTo(v)) return null; 33 Stack<Integer> path=new Stack<Integer>(); 34 for(int x=v;x!=s;x=edgeTo[x]) 35 { 36 path.push(x); 37 } 38 path.push(s); 39 return path; 40 } 41 42 43 }
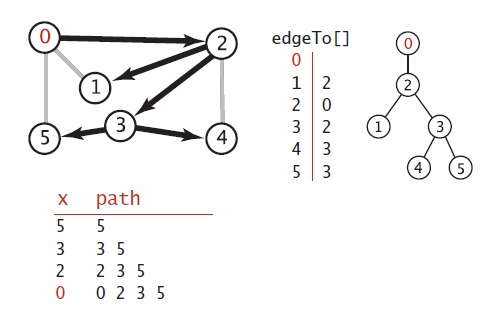
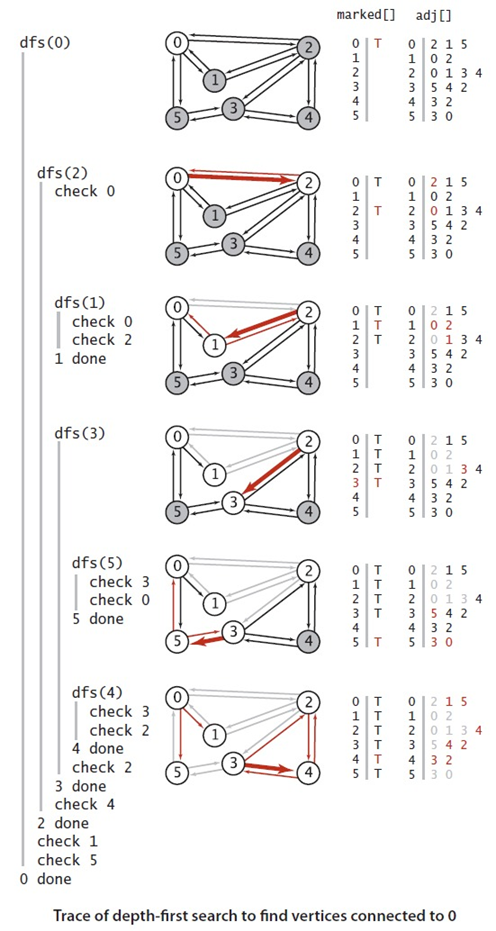
上图中是黑色线条表示深度优先搜索中,所有定点到原点0的路径,他是通过edgeTo[]这个变量记录的,可以从右边可以看出,他其实是一颗树,树根即是原点,每个子节点到树根的路径即是从原点到该子节点的路径。下图是深度优先搜索算法的一个简单例子的追踪。
算法行为追踪:
//通过遍历,我们想edgeTo[]数组中添加了0-2,2-1,2-3,3-5和3-4.具体分析和上面的分析类似,不再阐述。
广度优先遍历:
现在我们可以通过深度优先遍历来判断顶点S到顶点V是否存在路径,那么如果存在路径,能否找出最小的那一条的呢?事实上,深度优先遍历在解决这个问题上没有什么作用,因为它遍历图的顺序和找出最短路径的目标没有任何关系,而要解决这个问题,就需要用到广度优先遍历。
要找到S到V的最短路径,从S开始,在所有由一条边到达的定点中就可以寻找V,如果找不到就可以在与S距离两条边的所有顶点中招,以此类推。广度优先遍历就好像一条河流流向迷宫,当遇到交叉路口,河水会分开继续流动,而两股水流相遇时就会合成一股水流!
我们使用队列来实现相关功能。(用到的API请参考 )
此算法的核心步骤:
(1):取队列中的下一个顶点V并标记它
(2):将于V相邻的未被标记的顶点加入队列。
代码实现:

1 public class BreadthFirstSearch { 2 3 private boolean[] marked; 4 private int s; 5 private int edgeTo[]; 6 public BreadthFirstSearch(Graph g,int s) 7 { 8 marked=new boolean[g.V()]; 9 this.s=s; 10 edgeTo=new int[g.V()]; 11 bfs(g,s); 12 } 13 14 private void bfs(Graph g,int s) 15 { Queue<Integer> queue=new Queue<Integer>(); 16 marked[s]=true;//标记 17 queue.enqueue(s);//起点进队 18 19 while(!queue.isEmpty()) 20 { 21 int v=queue.dequeue(); 22 for(int w:g.adj(v)) 23 { 24 if(!marked[w]) 25 { edgeTo[w]=v; 26 marked[w]=true; 27 queue.enqueue(w); 28 } 29 } 30 } 31 32 } 33 34 public boolean hasPathTo(int v) 35 { 36 return marked[v]; 37 } 38 39 public Iterable<Integer> pathTo(int v) 40 { 41 if(!hasPathTo(v)) return null; 42 Stack<Integer> path=new Stack<Integer>(); 43 for(int x=v;x!=s;x=edgeTo[x]) 44 { 45 path.push(x); 46 } 47 path.push(s); 48 return path; 49 }//与深度优先遍历一样 50 51 52 }
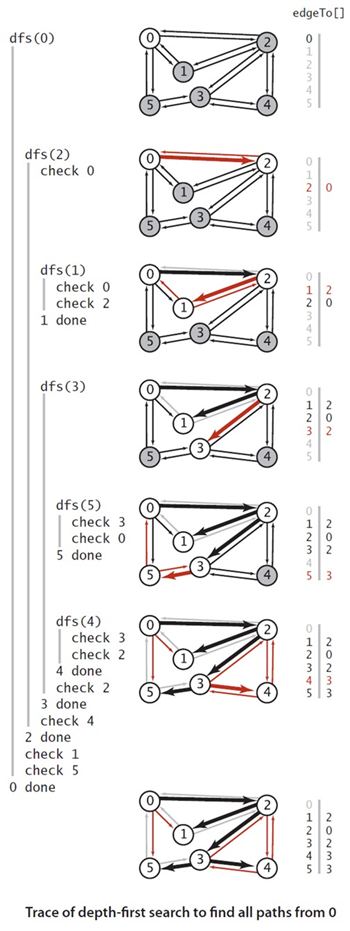
算法行为跟踪:
首先,标记开始顶点0,加入队列中。
(1),0出队,将他的邻居节点2、1、5依次标记并加入队列。将对应的edgeTo[]设为0;
(2)2出队,检查它的相邻 节点,发现0、1都已经被标记,将3、4标记并加入队列中,将3、4对应的edgeTo设为2;
(3)1出队,检查发现它的所有相邻节点都被标记了。
(4)5出队,检查发现它的所有相邻节点都被标记了。
(5)3出队,检查发现它的所有相邻节点都被标记了。
(6)4出队,检查发现它的所有相邻节点都被标记了。