数据结构之无向图

前言：  

      我们所讨论的图模型中，边仅仅是两个顶点之间的连接。一般使用0-(V-1)来表示一张含有V个顶点的图中的各个顶点。用v-w的记法表示v点和w点之间的边（又可以写成w-v）。

      特殊的两种图：

         自环：  一条连接一个顶点和其自身的边。

         平行边： 连接同一对顶点的两条边。

     以下所说的图两个顶点之间仅含有一条边。

相关术语：

  

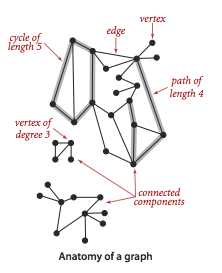
当边连接两个顶点时，我们说顶点彼此 相邻。

顶点的度数为依附于他的边的总数。

子图是一幅图所有被边的一个子集（包括他们所依附的顶点）。

路径是由边连接的顶点序列，没有重复的边。

简单路径是没有重复顶点的路径。

环是一条至少含有一条边且起点和终点相同的路径。

简单环是一条（除了起点和终点必须相同之外）不含重复顶点和边的环。

路径或环的长度为其包含的边数。

如果从任意一个顶点都存在一条路径到达另一个任意顶点，则称这幅图是连通图。

一个非连通图由若干连通图组成，它们都是极大连通子图。

无环图是一个不包含环的图。

树是一副无环连通图。互不相连的树组成森林。连通图的生成树是他的一副子图，它含有图中的所有顶点且是一颗树。图的生成森林是他的所有连通子图的生成树的集合。

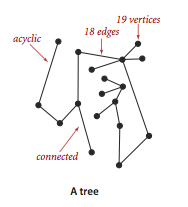
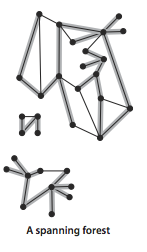
关于树的定义，以下五种说法是等价的：（一副含有V个顶点的图G）

1：G有V-1条边并且不含环。

2：G有V-1条边并且是联通的

3：G是连通的且删除任意一条边都会使他不连通。

4：G是无环图且添加任意一条边都会使他产生一条环。

5：G中任意一对顶点间仅存在一条简单路径。

 

我们定义以下图的基本操作API：

Public  class   Graph

                 Graph(int V)   //创建一个含有V个顶点但不含边的图

                 Graph(InputStream in) //从标准输入流中读取一个图

          int     V()    //顶点数

          int     E()    //边数

          void addEdge(int v,int w)  //添加边V-W

    Iterable<Integer> adj（int v）   //遍历与v相邻的顶点

           String toString()      // @Override

 

相关实现：

计算V的度数：

       public static int degree(Graph g,int v)

{    int  degree=0;

    for(int w: g.adj(v)) degree++;

   return degree;

}

计算所有顶点的最大度数：

   public static int maxDegree(Graph g)

{    int  max=0;

     for(int v=0;v<g.v();v++)

             if(degree(g,v)>max)

                   max=degree(g,v);

          return  max;   }

计算自环的个数：

public static int numberOfSefLoops(Graph g)

{   int count=0;

       for(int v=0;v<g.v();v++)

           for(int w:g.adj(v))

            if(w==v)  count++;

       return count/2;

}

//覆写toString方法@Override

  public String toString()

{

    String s=V+”vertices”+E+” edges\n”;//建议你用StringBuilder

       for(int v=0;v<g.v();v++)

        {   s+=v+”:  ”;

              for(int w:this.adj(v))

                 s+=“\n”;

}

   return  s;

}

 

图的几种表示方法：

要求：  1、必须为各种情况下遇到的图预留足够空间。

             2、快。

  邻接矩阵：

      用一个V * V的Boolean矩阵表示，1代表相连。

       //不满足第一种要求。

  边的数组：

       使用一个Edge类，含有两个int变量。

       /不满足第二个要求，比如调用adj方法。

  邻接表数组：（推荐）

      使用以顶点为索引的列表数组，其中每个元素都是和该顶点相连的顶点列表。如下图：

     

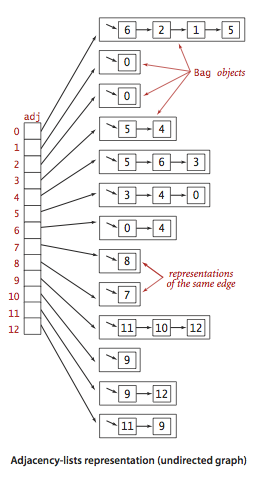
要连接一条v到w的边，我们要将w添加到v的邻接表中并把v添加到w的临界表中。因此这种结构中每条边都会出现两次。

  代码实现：

//我们使用前面介绍过的Bag,Stack实现，相关代码请看数据结构之队列、栈。

public class Graph {

    private final int V;
    private int E;
    private Bag<Integer> adj[];
    
    @SuppressWarnings("unchecked")
    public Graph(int V)
    {   if (V < 0) throw new IllegalArgumentException("Number of vertices must be nonnegative");
        this.V=V;
        this.E=0;
        adj= (Bag<Integer>[])new Bag[V];
        for(int i=0;i<V;i++)
        {
            adj[i]=new Bag<Integer>();
        }
    }
    
    public Graph(Graph G) {
        this(G.V());
        this.E = G.E();
        for (int v = 0; v < G.V(); v++) {
         
            Stack<Integer> reverse = new Stack<Integer>();
            for (int w : G.adj[v]) {
                reverse.push(w);
            }
            for (int w : reverse) {
                adj[v].add(w);
            }
        }
    }
    
    public int V()
    {
        return this.V;
    }
    
    public int E()
    {
        return this.E;
    }
    
    private void validateVertex(int v) {
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
    }
    
    public void addEdge(int v,int w)
    {  validateVertex(v);
       validateVertex(w);
     adj[v].add(w);    
     adj[w].add(v);
     E++;
    }
    
     public Iterable<Integer> adj(int v) {
            validateVertex(v);
            return adj[v];
        }
     
      public int degree(int v) {
            validateVertex(v);
            return adj[v].size();
        }
      
       public String toString() {
            StringBuilder s = new StringBuilder();
            s.append(V + " vertices, " + E + " edges " );
            for (int v = 0; v < V; v++) {
                s.append(v + ": ");
                for (int w : adj[v]) {
                    s.append(w + " ");
                }
                s.append("\r");
            }
            return s.toString();
        }

}