DS博客作业05--查找
| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业05--查找 |
| 这个作业的目标 | 学习查找的相关结构 |
| 姓名 | 李雷默 |
0.PTA得分截图


1.本周学习总结
1.1 查找的性能指标
- ASL即平均查找长度,在查找运算中,由于所费时间在关键字的比较上,所以把平均需要和待查找值比较的关键字次数称为平均查找长度。一个算法的ASL越大,说明时间性能差,反之,时间性能好。
- 顺序查找,时间复杂度O(N)
分块查找,时间复杂度O(logN+N/m);
二分查找,时间复杂度O(logN)
哈希查找,时间复杂度O(1)
1.2 静态查找
- 顺序查找:
![]()
![]()
- 二分查找:
ASL成功=每一层节点数层次数的总和/总结点数
ASL不成功=其他不存在于树中的每一层节点数(层次数-1)/总结点数
1.3 二叉搜索树
1.3.1 如何构建二叉搜索树(操作)
构建:把父节点设置为根节点。如果新节点内的数据值小于当前节点内的数据值,那么把当前节点设置为当前节点的左孩子。
如果新节点内的数据值大于当前节点内的数据值,那么就将当前节点设为当前节点的右孩子。
如果当前节点的左孩子的数值为空,就把新节点插入在这里并且退出循环。否则,跳到 while 循环的下一次循环操作中。
把当前节点设置为当前节点的右孩子。如果当前节点的右孩子的数值为空,就把新节点插入在这里并且退出循环。否则,跳到 while 循环的下一次循环操作中。
插入:树为空,则直接插入,返回true。树不为空,按二叉搜索树性质查找插入的位置,插入新节点
删除:
1.叶子节点则直接删除
2.若该节点,有一个节点,左或是右。因为只有一个节点,直接令祖父节点指向孙子节点,孙子节点的左右需要分开判断。
3.若该节点含有两个子节点,一般的删除策略是用其右子树的最小结点代替待删除结点的数据,然后递归删除那个右子树最小结点。即将第三种情况转化为第二种情况
1.3.2 如何构建二叉搜索树(代码)
- 构建:
STNode* CreateBST(KeyType A[], int n)//创建二叉排序树
//返回BST树根结点指针
{
BSTNode* bt = NULL;//初始时bt为空树
int i = 0;
while (i < n)
{
InsertBST(bt, a[i]);//插入,构建二叉树的实质是连续向二叉树插入若干个元素的过程
i++;
}
return bt;//返回建立的二叉排序树的根指针
}
- 插入:
bool InsertBST(BSTNode*& bt, KeyType k)
//在二叉排序树bt中插入一个关键字为k的结点,若插入成功返回真,否则返回假
{
if (bt == NULL)//原树为空,新插人的结点为根结点
{
bt = (BSTNode*)malloc(sizeof(BSTNode));
bt->key = k; bt->lchild - bt->rchild - NULL;
return true;
}
else if (k == bt->key)
return false;//树中存在相同关键字的结点,返回假
else if (k < bt->key)
return InsertBST(bt → > lchild, k);//插入到左子树中
else
return InsertBST(bt->rchild, k);//插入到右子树中
}
- 删除:
bool DeleteBST(BSTNode& bt, KeyType k)//在bt中删除关键字为k的结点
{
if (bt == NULL)
return false//空树删除失败,返回假
else
{
if (k < bt->key)
return DeleteBST(bt->lchild, k);//递归在左子树中删除为k的结点
else if (k > bt->key)
return DeleteBST(bt->rchild, k);//递归在右子树中删除为k的结点
else//找到了要删除的结点bt
{
Delete(bt);//调用Delete(bt)函数删除结点bt
return true;//删除成功,返回真
}
}
}
void Delete(BSTNode*& p)//从二叉排序树中删除结点p
{
BSTNode* q;
if (p->rchild == NULL) //结点p没有右子树(含为叶子结点)的情况
{
q = p;
p = p->lchild;//用结点p的左孩子替代它
free(q);
}
else if (p->lchild = NULL) //结点口没有左子树的情况
{
q = р;
p = p->rchild;//用结点p的右孩子替代它
free(q);
}
else Delete(p, p->lchild);//结点p既有左子树又有右子树的情况
}
void Deletel(BSTNode* p, BSTNode*& r) //被删结点p有左、右子树,r指向其左孩子
{
BSTNode* q;
if (r->rchild != NULL)
Deletel(p, r->rchild);//递归找结点r的最右下结点
else//找到了最右下结点r(它没有右子树)
{
p->key = r->key;//将结点r的值存放到结点p中(结点值替代)
P->data = r->data;
q = r;//删除结点r
r = r->lchild;//即用结点r的左孩子替代它
free(q);//释放结点a的空间
}
}
二叉树删除结点的顺序也是要先查找,再删除,与插入结点类似,二叉排序树插入时间复杂度最大为O(n)。若是二叉排序树比较平衡,其时间复杂度下降,最小的时间复杂度为O(logn)。
1.4 AVL树
-
AVL树解决什么问题,其特点是什么
平衡二叉树又称为 AVL 树,其实就是一颗平衡的二叉排序树 ,解决了二叉排序树的不平衡问题,即斜树。AVL树或者是一颗空树,或者是具有下列性质的二叉排序树:
它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过 1。
平衡二叉树上结点的 平衡因子定义为该结点的左子树深度减去它的右子树的深度,平衡二叉树上所有结点的平衡因子只可能是 -1,0,1。
AVL树是从二分搜索树升级过来的。所以它满足二分搜索树的基本特征【左子树所有节点都小于其根节点,右子树所有节点都大于其根节点】,AVL树是对于二分搜索树退化成链表的一种解决方案。 -
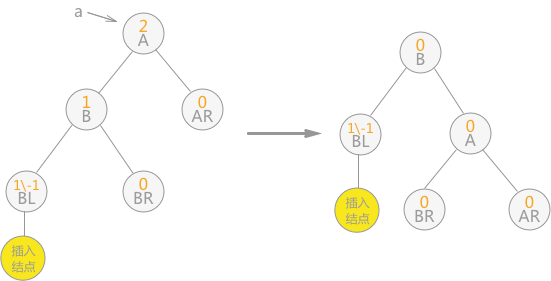
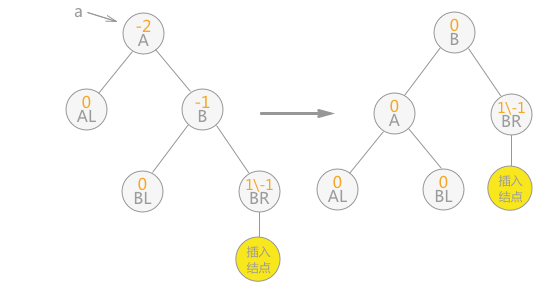
rr型:
![]()
ll型:
![]()
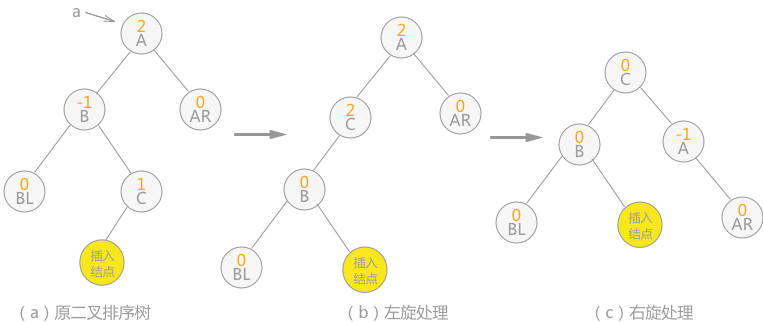
lr型:
![]()
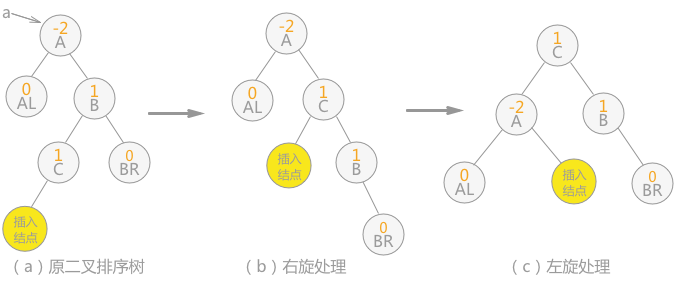
rl型:
![]()
-
AVL树的高度和树的总节点数n的关系:
AVL树,它的特点是在二叉搜索树的基础上,要求每个节点的左子树和右子树的高度差至多为1。这个要求使AVL的高度h = log2 n.(n为树的结点个数) -
介绍基于AVL树结构实现的STL容器map的特点、用法。
map容器的常用操作
map<Key, value> m
map<Key, value> m; 构造一个空的map,
empty() // 如果map 为空,返回true。否则返回 false
ize() // 返回map 中元素的大小,即 key-value 的个数
操作符[] // m[k] 返回map 中 Key为 k的元素的value的引用。
// 如果 k不存在,那么将会插入一个 key为 k的元素,并返回其默认 value。
// []操作总会将 map的大小 +1
find 查找 在map中查找key 为 k的元素,返回指向它的迭代器。若k不存在,返回 map::end.
count 计数 统计map中 key为k的元素的个数,对于map,返回值不是1(存在),就是0(不存在)
1.5 B-树和B+树
-
B-树和AVL树区别
B-树每个节点可以有多个关键字,而AVL树每个节点只能有一个关键字。同时,B-树可以有多个子树,而AVL树只能最多有两个子树。
B-树是一棵多叉平衡搜索树,旨在比AVL树能够拥有更低的树高,提高查找的效率,但是同AVL树一样,面对插入和删除数据的操作后需要维持平衡,这可能带来一些得不偿失的情况。其次B-树可以被采用在外存的数据查询上,因为树高比较低,这样就可以减少磁盘的I/O次数。 -
B-树定义:
1.树中每个结点至多有m 棵子树(孩子节点);
2.若根结点不是叶子结点,则至少有 2 棵子树;
3.除根之外的所有节点至少有 m/2孩子节点;
4.所有的叶子结点都出现在同一层次上,并且不带信息,通常称为失败结点
5.所有的非终端结点最多有 m一1 个关键字 -
插入:
1.该结点的关键字数目n<m-1,不修改指针
2.该结点的关键字数目n=m-1,则需进行结点分裂
1)如果没有双亲结点,新建一个双亲结点,树的高度增加一层
2)如果有双亲结点,将ki插入到双亲结点中 -
删除:
1.结点中关键字的个数>[m/2]-1,直接删除
2.结点中关键字的个数=[m/2]-1
1)要从其左(或右)兄弟结点"借调"关键字
2)若其左和右兄弟结点均无关键字可借(结点中只有最少量的关键字),则必须进行结点的"合并" -
B+树定义:
索引文件组织中,经常使用B-树的变形B+树,B+树是大型索引文件的标准组织方式。
一棵m阶B+树满足下列条件:
1.每个分支节点至多有m棵子树
2.根节点或者没有子树,或者至少有两棵子树
3.除根节点,其他每个分支节点至少有「m/2]棵子树
4.有n棵子树的节点有n个关键字。
5.所有叶子结点包含全部关键字及指向相应记录的指针
a.叶子结点按关键字大小顺序链接
b.叶子结点时直接指向数据文件的记录
6.所有分支结点(可以看成是分块索引的索引表),包含子节点最大关键字及指向子节点的指针
1.6 散列查找
-
哈希表的构造
1.直接定址法
哈希函数:h(k)=k+c
优势:计算简单,不可能有冲突发生
缺点:关键字分布不连续,将造成内存单元的大量浪费
2.除留取余数法
用关键字k除以某个不大于哈希表长度m的数p所得的余数作为哈希地址,h(k)=k%p(这里的p最好为不大于m的质数,减少冲突的可能性) -
哈希冲突解决
1.开放定址法
在出现哈希冲突时,再哈希表中找到一个新的空闲位置存放元素,例如:要存放关键字k,d=h(k),而地址d已经被其他元素占用了,那么就在d地址附近寻找空闲位置进行填入。开放定址法分为线性探测和平方探测等
2.线性探测
线性探测是从发生冲突的地址d0开始,依次探测d0的下一个地址(当到达哈希表表尾时,下一个探测地址为表首地址0),直到找到一个空闲的位置单元为止,探测序列为:d=(d+i)%m,所以,我们在设置哈希表的长度时一定要大等于元素个数,保证每个数据都能找到一个空闲单元插入 -
哈希表ASL:
![]()
-
哈希链ASL:
![]()
![]()
2.PTA题目介绍
2.1 是否完全二叉搜索树
2.1.1 伪代码
void InserBST(BinTree*& BST,KeyType k)//往二叉树中插入结点k
{
if(BST==NULL) 建立新结点;
else if(k<BST->key) 递归进入右子树;
else 递归进入左子树
}
/*层次遍历二叉树并判断是否为完全二叉树*/
bool Level_DispBST(BinTree* BST)
{
定义变量end表示是否已经找到第一个叶子结点或者第一个只有左孩子结点;
(如果是,则接下来未遍历的结点应该都是叶子结点)
定义flag保存判断结果;
若根结点BST不为空,入队,并输出;
while(队不为空)
出队一个结点p;
若结点p的左,右孩子不为空,依次输出,并入队;
若在剩余节点都应该是叶子结点的情况下p为非叶子节点
不是完全二叉树,flag=flase;
若结点p只有右孩子,没有左孩子
不是完全二叉树,flag=flase;
若结点p为叶子结点或者为第一个只有左孩子的结点
修改end,表示接下来应该都是叶子结点;
end while
return flag;
}
2.1.2 提交列表

2.1.3 本题知识点
完全二叉树的结构,二叉树的层次遍历,二叉搜索树的插入操作
2.2 航空公司VIP客户查询
2.2.1 伪代码
map<string, int>M;
for i=0 to n-1 i++
输入身份证,已行驶里程数据
if 里程小于最小里程k
then 让里程=k
end if
if 该身份证已由会员记录
then 原来的里程数再加上刚才输入的(M[id1]+=len)
end if
else 未被登记为会员
则现在输入身份证及里程信息(M[id1]=len)
end for
for i=0 to m-1 i++
输入身份证
若信息库(M)里由=有该身份证信息就输出里程信息
若信息库M中未找到该身份证信息
则输出“NO INFO
2.2.2 提交列表
2.2.3 本题知识点
哈希链的创建,初始化,查找和插入
2.3 基于词频的文件相似度
2.3.1 伪代码
定义一个map二维数组,一维表示文件序号,二维表示该文件某个单词,值表示出现了几次
for i=1 to N i++
while 读取一行的内容,当内容为#就停止循环
令top=0;
for j=0 to s.length() j++
if 内容不是字母即为分割符
then if 单词长度小于3 则不记录
end if
continue
end if
if 单词长度大于10
then 值记录前10
end if
else 加结束符 单词数+1
top=0
end if
else 是字母,大写该小写
需要队组后一个单词判断
开始计算相似度:
输入两个文件序号
map<string, int>:: iterator itl,it2//两个迭代器,类似指针
因为map可以自动排序(按照字典序),所以可以两个文本同时遍历
itl->first<it2->first 说明itl后面可能有和it2相同的单词itl向后移
itl->first>it2->first 说明it2后面可能有和itl相同的单词itl向后移
相同时,将分子++,两个迭代器都向后移
输出相似度 100.0*mole/(deno-mole)
2.3.2 提交列表

2.3.3 本题知识点
字符串的遍历,string的使用
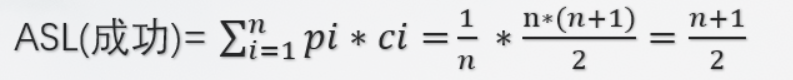





 浙公网安备 33010602011771号
浙公网安备 33010602011771号