DS博客作业02-栈和队列
| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业02-栈和队列 |
| 这个作业的目标 | 学习栈和队列的结构设计及运算操作 |
| 姓名 | 李雷默 |
0.PTA得分截图
1.本周学习总结
1.1 栈
1.1.1顺序栈
顺序表（底层实现是数组）和栈结构的存储数据的方式高度相似，只不过栈对数据的存取过程有特殊的限制，而顺序表没有。
- 进栈
bool Push(SqStack &S,ElemType e)
{
if(s->top==MaxSize-1)//顺序栈进栈时要注意栈是否已满
{
return false;
}
s->top++;
s->data[s->top]=e;
return true;
}
- 出栈
bool Pop(SqStack &s,ElemType &e)
{
if(s->top==-1)//顺序栈出栈时要注意栈是否为空
{
return flase
}
e=s->data[s->top];
s->top--;
return ture;
}
}
1.1.2链栈
链表的头部作为栈顶，意味着：
- 在实现数据"入栈"操作时，需要将数据从链表的头部插入；
- 在实现数据"出栈"操作时，需要删除链表头部的首元节点；
因此，链栈实际上就是一个只能采用头插法插入或删除数据的链表。
- 进栈
void Push(LiStack &s,Elemtype e)
{
LiStack p;
p=new LiNode;
p->data=e;//头插法
p->next=s->next;
s->next=p;
};
}
出栈
bool Pop(LiStack &s,ElemType &e)
{
LiStack p;//新建结点临时保存
if(s->next=NULL)
{
return false;
}
p=s->next;
e=p->data;
s->enxt=p->next;
delete p;
return true;
}
1.2栈的应用
中缀表达式转化为后缀表达式：
中缀表达式a + b*c + (d * e + f) * g，其转换成后缀表达式则为a b c * + d e * f + g * +。
过程如下：
- 如果遇到操作数，我们就直接将其输出。
- 如果遇到操作符，则我们将其放入到栈中，遇到左括号时我们也将其放入栈中。
- 如果遇到一个右括号，则将栈元素弹出，将弹出的操作符输出直到遇到左括号为止。注意，左括号只弹出并不输出。
- 如果遇到任何其他的操作符，如（“+”， “*”，“（”）等，从栈中弹出元素直到遇到发现更低优先级的元素(或者栈为空)为止。弹出完这些元素后，才将遇到的操作符压入到栈中。有一点需要注意，只有在遇到" ) "的情况下我们才弹出" ( "，其他情况我们都不会弹出" ( "。
- 如果我们读到了输入的末尾，则将栈中所有元素依次弹出。
1.3队列
1.3.1顺序队列
顺序队列的底层使用的是数组，因此需预先申请一块足够大的内存空间初始化顺序队列。除此之外，为了满足顺序队列中数据从队尾进，队头出且先进先出的要求，我们还需要定义两个指针（front 和 rear）分别用于指向顺序队列中的队头元素和队尾元素。
- 进队列
bool enQueue(SqQueue &q,ElemType e)
{
if(q->rear+1==MaxSize)//判断是否栈满
return flase;
q->rear=q->rear+1;
q->data[q->rear]=e;
return ture;
}
- 出队列
bool deQueue(SqQueue &q,Elemtype &e)
{
if(q->front==q->rear)//判断队是否为空
return flase;
e=q->data[q->front];
q->front=q->front+1;//移动指针
return ture;
}
1.3.2环形队列
- 进队列
bool enQueue(SqQueue &q,Elemtype e)
{
if((q->rear+1)%MaxSize==q->front)//判断是否队满
return false;
q->rear=(q->rear+1)%MaxSize;//移动rear
q->data[q->rear]=e;
return true;
}
- 出队列
bool enQueue(SqQueue &q,Elemtype e)
{
if((q->rear+1)%MaxSize==q->front)//判断是否队满
return false;
q->rear=(q->rear+1)%MaxSize;//移动rear
q->data[q->rear]=e;
return true;
}
1.3.3链队列
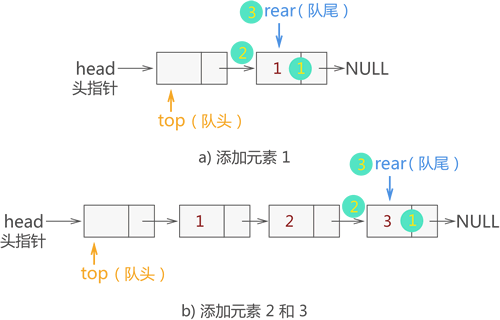
- 进队列
bool enQueue(LinkQuNode &q,ElemType e)
{
p=new QNode;
p->data=e;
p->next=NULL;
q->rear->next=p;
q->rear=p;
}
- 出队列
bool deQueue(LinkQuNode &q,ElemType e)
{
Node t;
if(q->rear==NULL)
return false;
t=q->front;
if(q->front==q->rear）
{
q->front=q->rear=NULL;
}
else
{
q->front=q->front->next;
}
e=t->data;
delete t;
}
1.3.4队列应用
7-5 jmu-报数游戏
2.PTA实验作业
2.1 7-2 jmu-ds-符号配对
2.1.1解题思路及伪代码
for(i = 0;i<len;i++)
{
if(s[i]!='{' && s[i]!='[' && s[i]!='(' && s[i]!='}' && s[i]!=']' && s[i]!=')' )//确认左符号是否满足条件，满足函数继续
continue;
if(s[i]=='{' || s[i] == '[' || s[i] == '(')
q.push(s[i]);
else if(s[i]==']' || s[i]==')'||s[i]=='}')
{
if(q.empty())//确认右符号
break;
else
{
if( (s[i]==']'&&q.top()=='[') || (s[i]==')'&&q.top()=='(') || (s[i]=='}'&&q.top()=='{') )
q.pop();
}
}
}
2.1.2 总结解题所用的知识点
本题需要考虑到左符号剩余，右符号剩余，配对情况，不配对情况，需要多重if 来进行约束判断，最后根据len的值输出对应的结果。
2.2 银行业务队列简单模拟
2.2.1 解题思路及伪代码
while(i<N)
{
cin >> num;
if(num%2==0)
{
evenQu.push(num);
}
else
{
oddQu.push(num);
}
i++;
}
int flag=0;
if(oddQu.size()!=1&&evenQu.size()!=1)
{
while(!evenQu.empty()&&!oddQu.empty())
{
if(flag==0)
{
cout << oddQu.front();
flag = 1;
}
else
{
cout<<' '<< oddQu.front();
}
oddQu.pop();
cout<<' '<<oddQu.front();
oddQu.pop();
cout<<' '<<evenQu.front();
evenQu.pop();
}
}
else
{
if(evenQu.size()==1)
{
cout<<evenQu.front();
evenQu.pop();
}
if(oddQu.size()==1)
{
cout<<oddQu.front();
oddQu.pop();
}
}
2.2.2总结解题所用的知识点
queue相关函数的使用、队列优先输出的顺序、本题需要考虑A对列的特殊情况，考虑其个数以及奇偶性。
3.阅读代码
3.1题目及解题代码
class MyQueue {
private:
stack<int> inStack, outStack;
void in2out() {
while (!inStack.empty()) {
outStack.push(inStack.top());
inStack.pop();
}
}
public:
MyQueue() {}
void push(int x) {
inStack.push(x);
}
int pop() {
if (outStack.empty()) {
in2out();
}
int x = outStack.top();
outStack.pop();
return x;
}
int peek() {
if (outStack.empty()) {
in2out();
}
return outStack.top();
}
bool empty() {
return inStack.empty() && outStack.empty();
}
};
3.2 该题的设计思路及伪代码
队列的特性是 FIFOFIFO（先入先出），而栈的特性是 FILOFILO（先入后出）。
知道两者特性之后，我们需要用两个栈来模拟队列的特性，一个栈为入队栈，一个栈为出对栈。
当出队栈存在内容时，出队栈的栈顶，即为第一个出队的元素。
若出队栈无元素，我们的需求又是出队的话，我们就需要将入队栈的内容反序导入出队栈，然后弹出栈顶即可。
3.3 分析该题目解题优势及难点
优势：代码简洁清晰，便于阅读。
难点：含有没教过的知识点，理解难度较大。
