弦图与区间图
弦图 - OI Wiki 这部分 OI-Wiki 上写的很好,证明也很妙。
弦图
弦:指一个大于 \(3\) 个点的环中,连接不相邻的两个点的边。非常形象。
弦图:指图中任意环均有弦。显然弦图的点导出子图也是弦图。
团:一个诱导子图满足对于子图内的点是完全图。非常形象。
单纯点:设 \(N(v)\) 表示 \(v\) 的邻域,一个点称为单纯点当且仅当 \(v+N(v)\) 的导出子图为一个团。
引理:任何一个弦图都至少有一个单纯点,不是完全图的弦图至少有两个不相邻的单纯点。
完美消除序列:一个点的序列 \(v_1,v_2,\cdots,v_k\) 满足 \(v_i\) 在 \(\{v_i,v_{i+1},\cdots,v_k\}\) 的导出子图中为一个单纯点。
定理:一个无向图是弦图当且仅当它有一个完美消除序列。
记
\(\omega(G)\) 为最大团的点集大小,称为团数。
\(\chi(G)\) 为最小染色的色数,称为色数。
\(\alpha(G)\) 为最大独立集的大小。
\(\kappa(G)\) 为最小团覆盖的团的数量。
\(\omega(G)\le \chi(G)\),因为最大团中颜色必须互不相同。
\(\alpha(G)\le\kappa(G)\),因为每个团中最多取一个点。
弦图的判定
MCS 算法
最大势算法 \(Maximum\ Cardinality\ Search\),可以在 \(O(n+m)\) 的时间内求出无向图的完美消除序列。
逆序从 \(n\) 到 \(1\) 把节点编号,编号为 \(i\) 的点出现在完美消除序列的第 \(i\) 个。
设 \(label_x\) 表示 \(x\) 与多少个已经标号的点相邻,每次选择 \(label\) 最大的未标号节点进行标号。
实现可以用链表维护对于每个 \(i\),满足 \(label_x=i\) 的 \(x\)。
每条边对 \(\sum\limits_{i=1}^n label_i\) 的贡献最多是 \(2\),时间复杂度为 \(O(n+m)\)。
非弦图时要判断每个点是否与后面相邻的点构成团,设 \(v_{j1}\cdots v_{jk}\) 是 \(i\) 连向后面的点。继承后面点的判断后,算法只需判断 \(v_{j1}\) 是否与其他 \(v_{j}\) 都相连即可。时间复杂度 \(O(n+m)\)。
于是我们可以在 \(O(n+m)\) 的时间复杂度内判断图是否是弦图并求出它的完美消除序列。
证明
只需证明求得序列中任意一点的后面与它相连的点两两相连。
设 \(p_i\) 为 \(i\) 在序列中的位置。
引理一:考虑三个点 \(u,v,w\) 且 \(p_u<p_v<p_w\),如果 \(uw\) 相连,\(vw\) 不相连,则 \(w\) 只给 \(u\) 的 \(label\) 贡献。为了让 \(v\) 比 \(u\) 先入序列,需要一个 \(x\) 满足 \(p_v<p_x\) 且 \(vx\) 相连,\(ux\) 不相连。
引理二:任意一个弦图一定不存在一个序列 \(v_0,v_1,\cdots,v_k(k\le 2)\) 满足下列性质
- \(v_iv_j\) 相连当且仅当 \(|i-j|=1\)。
- \(p_{v_0}>p_{v_i}(i\in [1,k])\)。
- 存在 \(i\in[1,k-1]\),满足 \(p_{v_i}<p_{v_{i+1}}<\cdots<p_{v_{k}}\) 且 \(p_{v_i}<p_{v_{i-1}}<\cdots<p_{v_1}<p_{v_{k}}<p_{v_0}\)。
证明引理:
由于 \(p_{v1}<p_{v_k}<p_{v_0}\),且 \(v_1v_0\) 相连,\(v_kv_0\) 不相连,所以由引理一,存在 \(x\) 满足 \(p_{v_k}<p_x\) 且 \(v_kx\) 相连,\(v_1x\) 不相连。
考虑最小的 \(j\in (1,k]\) 满足 \(v_jx\) 相连,那么 \(v_0x\) 不相连,否则 \(v_0v_1\cdots v_jx\) 构成长度大于 \(4\) 且无弦的环。
如果 \(p_x<p_{v_0}\),则 \(v_0,v_1,\cdots,v_j,x\) 是满足性质的序列;如果 \(p_{v_0}<p_x\) 则 \(x,v_j,\cdots,v_1,v_0\) 是满足性质的序列。
在上面的推导中,我们扩大了 \(p_{v_k}\),于是一直推下去,一定在第一步找不到 \(p_x>p_{v_k}\),产生矛盾。
证明原命题:
考虑三个点 \(u,v,w\) 且 \(p_u<p_v<p_w\),我们需要证明若 \(uv\) 相连,\(uw\) 相连,则 \(vw\) 一定相连。
反证,假设不相连,那么 \(w,u,v\) 就满足引理二中的性质,所以矛盾。
弦图的极大团
设 \(i\) 在弦图的完美消除序列中第 \(p_i\) 个。令 \(N(v)=\{w|p_w>p_v且w与v相连\}\)。
定理:弦图的极大团一定是 \(v\cup N(v)\) 的形式。
证明:设 \(v\) 为极大团 \(V\) 中 \(p\) 最小的点,那么 \(V\sube v\cup N(v)\),又 \(V\) 极大,得证。
推论:弦图最多有 \(n\) 个极大团。
要求出最多 \(n\) 个极大团,可以判断每个 \(x+N(x)\) 是否是极大团。
设 \(A=x+N(x),B=y+N(y)\),若 \(A\sub B\),则 \(A\) 不是极大团。此时显然 \(p_y<p_x\)。
那么设 \(nxt_x\) 表示 \(N(x)\) 中最靠前的点,\(y'\) 表示所有满足 \(A\sub B\) 的 \(y\) 中最靠后的点。此时必有 \(nxt_{y'}=x\),否则 \(y'\) 不是最靠后的,令 \(y'=nxt_{y'}\) 仍满足。
\(A\sub B\) 当且仅当 \(|A|+1\le |B|\)。
判断不是极大团转化为判断是否存在 \(y\),满足 \(p_y<p_x,nxt_y=x\) 且 \(|N(x)|+1\le |N(y)|\),时间复杂度 \(O(n+m)\)。实现参考 OI-Wiki。
弦图的团数或色数
团数 \(\omega(G)\),最大团的点集大小。
色数 \(\chi(G)\),相邻点不同色的最小颜色数。
定理:\(\omega(G)=\chi(G)\)。
一种构造方式:按完美消除序列从后往前依次给每个点染色,给每个点染上可以染的最小颜色,因为一个点只需要考虑在它后面的相连点的颜色。
设染色共用 \(t\) 种,那么该过程中 \(t\ge \chi(G)\) 而 \(t=\omega(G)\),又因为每个团内点颜色互不相同所以 \(\chi(G)\ge \omega(G)\) 所以 \(t=\chi(G)=\omega(G)\)。
弦图的最大独立集或最小团覆盖
最大独立集 \(\alpha(G)\),选出两两不相邻的点的最大点集。
最小团覆盖 \(\kappa(G)\),用团覆盖整张图的最小团数。
定理:\(\alpha(G)=\kappa(G)\)。
构造最大独立集的方式:完美消除序列从前往后能选就选。
设最大独立集为 \({v_1,v_2,\cdots,v_t}\),则团的集合 \(\{\{v_1+N(v_1)\},\{v_2+N(v_2)\},\cdots,\{v_t+N(v_t)\} \}\) 是图的最小团覆盖。
因为若没有覆盖完那么剩下的点是独立点,与最大独立集矛盾。
而 \(t\le \alpha(G),t\ge\kappa(G)\),又因为每个团里都能选一个所以 \(\kappa(G)\ge \alpha(G)\),所以 \(\alpha(G)=\kappa(G)\)。
完美图
完美图:一个图 \(G\) 的每一个诱导子图(点导出子图)都满足 \(\omega(G)=\chi(G)\)。
伴完美图:一个图 \(G\) 的每一个诱导子图(点导出子图)都满足 \(\alpha(G)=\kappa(G)\)。
完美图等价于伴完美图。
弦图属于完美图。
区间图
给定一些区间,定义一个相交图为每个顶点表示一个区间,两个点有边当且仅当两个区间的交集非空。
一个点为区间图当且仅当它是若干个区间图的相交图。
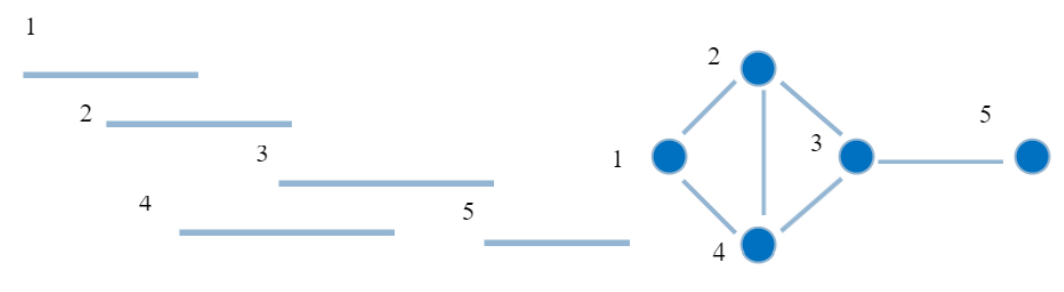
性质
区间图一定是弦图,显然不存在长度大于 \(3\) 的无弦环。于是区间图具有弦图的一切性质。
区间图的一个完美消除序列是将所有区间按照右端点从小到大排序。显然右边所有与当前区间有交的区间之间都相交。
应用
-
给定 \(n\) 个区间,要求选择最多区间而不互相重叠。
- 区间图的最大独立集。
-
有 \(n\) 个高为 \(1\),宽为 \([L_i,R_i]\) 的积木,求一个下落顺序使最后积木总高度最小。
- 把一层积木看成一个颜色,转化为区间图的色数问题。

