后缀自动机
后缀自动机 SAM
昨天看了一晚上今天有些感性理解，记一下。
SAM 是什么样的
endpose
是指一个子串在原串中的所有结束位置的集合。比如 \(ababc\) 中子串 \(ab\) 的 endpose 是 \(\{2,4\}\)。
将字符串 \(S\) 所有子串及其 endpose 写出来，可以发现一些等价类，即 endpose 相同的一些子串，如上文中 \(ab\) 和 \(b\) 是一个等价类，因为他们的 endpose 相同。
注意到 endpose 存在包含关系但不存在相交，这是因为一旦存在一个交，就说明一个子串是另一个的后缀。
不同等价类之间根据包含关系构成一棵树，树根是虚拟节点 \(t\)，定义其 endpose 为 \(\{1,\cdots,n\}\)，记等价类儿子向父亲的链接为 \(link\)。
从一个等价类向上走时 endpose 不断增大，此时他的祖先都是等价类中子串的后缀且长度逐渐变小。
如果设一个等价类中最长的子串长为 \(len\)，最短子串长为 \(minlen\)，那么一个等价类中包含长度为 \([minlen,len]\) 的后缀，且其父亲和他的长度是连续的，即 \(minlen=len_{link}+1\)。
转移
不同于 endpose 之间的父子关系，转移是指在一个子串后加上一个字符到达另一个子串。显然转移是在等价类之间进行的，因为等价类的 endpose 在位置上减一后就能到达其他的一些不同等价类，于是转移会形成从 \(t\) 开始的一张 DAG。
等价类中一条祖先链上的子串是一连串的后缀，而转移连向的则是一个前缀对应的不同子串。
后缀自动机就由等价类，等价类父子 \(link\) 和转移构成。
形象化的，\(abcbc\) 的 SAM 是这样（其中红边为转移，黑边为 \(link\)）
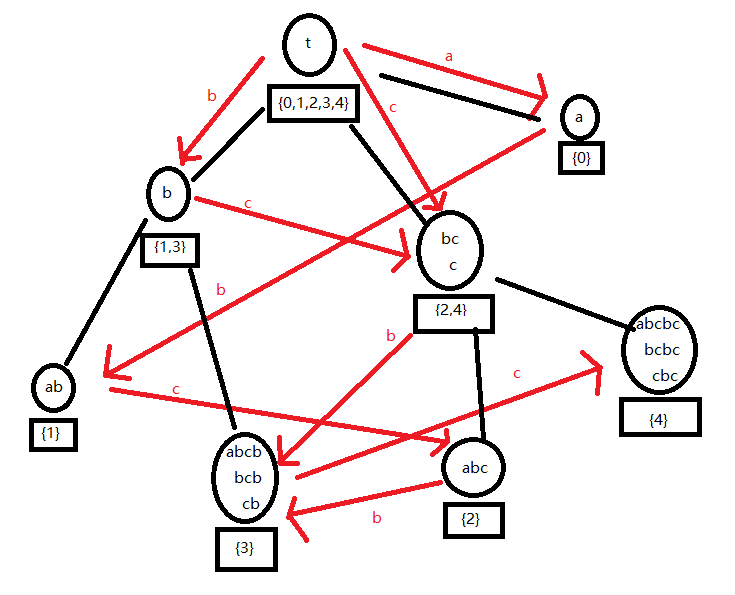
转移可能略过混乱（
然后我们可以肉眼看到的性质
是一条从等价类沿 \(link\) 走到根节点的路径上的所有串是原串某子串的所有后缀。
原串的任意子串都可以通过转移走到。
肉眼看不出来的是 SAM 的转移数是线性的，上界为 \(3n-4\)；等价类数是线性的，上界为 \(2n-1\)，这使得 SAM 成为了一个强大的解决字符串问题的工具。
如何构造 SAM
给出在线线性构造 SAM 的方法。
我们增添一个字符到原字符串，并在原有的 SAM 上进行修改。
记增添前原串所在等价类为 \(last\)。
现在我们新增一个节点 \(cur\) 代表的是新增字符后的原串所在等价类，此时原串所有后缀都在 \(cur\) 中。
接下来我们发现 \(last\) 是向 \(cur\) 有新增字符 \(c\) 的转移的，包括 \(last\) 的所有祖先也有转移。
我们遍历 \(last\) 的祖先 \(p\) 直到 \(p\) 已经有 \(c\) 的转移，记转移到的点为 \(q\)，也就是说，现在 \(cur\) 中有了曾经出现过的子串，那么显然我们应该把 \(cur\) 的 \(link\) 设为 \(q\)，这意味着 \(cur\) 到 \(q\) 到根 \(t\) 形成了连续的一串后缀。
注意到 \(cur\) 中该出现过的子串可由 \(p\) 转移到 \(q\)，但 \(q\) 中可能不只含有这个重复的子串，\(q\) 可能是一段连续后缀，而这个重复的串只是其中一部分。于是我们注意到新的 \(cur\) 的出现将会改变 \(q\) 内这个重复子串以上的串的 endpose，所以我们需要把 \(q\) 拆开，我们复制 \(q\) 的 \(link\) 和转移到 \(clone\)，并将 \(len_{clone}\) 设为 \(len_p+1\) 表示重复串以上的所有串，我们再将 \(q\) 和 \(cur\) 的 \(link\) 定向到 \(clone\)。最后再把所有存在转移到 \(q\) 的重复部分的点重转移到 \(clone\)，由于 \(p\) 可以转移到 \(q\) 的重复部分，所以所有需要改转移的点都在 \(p\) 的祖先链上。
而如果 \(q\) 中不存在比重复串更长的串，我们就可以直接把 \(cur\) 的 \(link\) 定向到 \(clone\)，这里的判断依据是 \(len_p+1=len_q\)。
添加完成后，将 \(last\) 改为 \(cur\)。
如何实现
定义一个存储等价类的结构体
struct state{
int len,link,siz;
map<char,int>nxt;
}st[N<<1];
定义当前总等价类数 \(sz\) 和 当前原串所在等价类 \(last\)
int sz,last;
定义 SAM 初始化 \(t\)（\(link=-1\) 为边界）
void sum_init(){st[0].len=0,st[0].link=-1,sz++,last=0;}
定义在原 SAM 上添加字符的操作
void sum_extend(char c){
int cur=sz++;
st[cur].len=st[last].len+1,st[cur].siz=1;
int p=last;
while(p!=-1&&!st[p].nxt.count(c))
st[p].nxt[c]=cur,p=st[p].link;
if(p==-1)st[cur].link=0;
else{
int q=st[p].nxt[c];
if(st[p].len+1==st[q].len)st[cur].link=q;
else{
int clone=sz++;
st[clone].len=st[p].len+1;
st[clone].link=st[q].link;
st[clone].nxt=st[q].nxt;
while(p!=-1&&st[p].nxt[c]==q)
st[p].nxt[c]=clone,p=st[p].link;
st[q].link=st[cur].link=clone;
}
}
last=cur;
}
如何做题
（没看懂时间复杂度证明直接做题的屑）
模板题，将 SAM 建出后考虑如何计数。
注意到只需要求出每个等价类的出现次数，于是我们只需要让所有原串前缀所在等价类记 \(siz\) 为 \(1\)，并在 SAM 上求一下子树的 \(siz\) 和即可。这是因为所有前缀所在等价类向祖先的贡献就相当于对所有前缀枚举后缀，相当于枚举了原串的所有子串。
const int N=1000005;
struct state{
int len,link,siz;
map<char,int>nxt;
}st[N<<1];
int sz,last;
void sum_init(){st[0].len=0,st[0].link=-1,sz++,last=0;}
void sum_extend(char c){
int cur=sz++;
st[cur].len=st[last].len+1,st[cur].siz=1;
int p=last;
while(p!=-1&&!st[p].nxt.count(c))
st[p].nxt[c]=cur,p=st[p].link;
if(p==-1)st[cur].link=0;
else{
int q=st[p].nxt[c];
if(st[p].len+1==st[q].len)st[cur].link=q;
else{
int clone=sz++;
st[clone].len=st[p].len+1;
st[clone].link=st[q].link;
st[clone].nxt=st[q].nxt;
while(p!=-1&&st[p].nxt[c]==q)
st[p].nxt[c]=clone,p=st[p].link;
st[q].link=st[cur].link=clone;
}
}
last=cur;
}
string S;
int cnt[N<<1],t[N<<1];
ll ans;
signed main(){
cin>>S;
sum_init();
for(int i=0,R=S.length();i<R;i++)sum_extend(S[i]);
for(int i=1;i<sz;i++)cnt[st[i].len]++;
for(int i=1;i<sz;i++)cnt[i]+=cnt[i-1];
for(int i=1;i<sz;i++)t[cnt[st[i].len]--]=i;
for(int i=sz-1;i>0;i--){
int p=t[i];st[st[p].link].siz+=st[p].siz;
if(st[p].siz>1)ans=max(ans,1ll*st[p].siz*st[p].len);
}
cout<<ans;
return 0;
}
