决策单调性优化dp
决策单调性优化属于常见 1D/1D 型 dp 优化。
1D/1D 型 dp 指转移式为 \(dp[i]=\max/\min\{dp[j]+w[j,i]\}+g[i],j\in[L,R]\)
其中 \(w[j,i]\) 指从 \(j\) 转移到 \(i\) 的贡献。
如果 \(w[i,j]\) 可以拆成只与 \(h[i],h[j]\) 有关,那么可以使用单调队列优化。时间复杂度为 \(O(n)\)。
如果 \(w[i,j]\) 可以拆成只与 \(h[i],h[j],h[i]*h[j]\) 有关,那么可以使用斜率优化。时间复杂度为 \(O(n)\) 或 \(O(n\log n)\)。
如果 \(w[i,j]\) 满足四边形不等式即 \(a\le b\le c\le d,w[a,c]+w[b,d]\) 优于 \(w[a,d]+w[b,c]\),那么可以使用决策单调性优化。时间复杂度为 \(O(n\log n)\)。
决策单调性就是指对于 \(a\le b\le c\le d\),若从 \(b\) 转移到 \(c\) 比从 \(a\) 转移到 \(c\) 更优,那么一定从 \(b\) 转移到 \(d\) 也比从 \(a\) 转移到 \(d\) 更优。
也就是决策点单调不降。
也就是 \(f[b]+w[b,c]\le f[a]+w[a,c] \Rightarrow f[b]+w[b,d]\le f[a]+w[a,d]\)
发现只要有 \(w[b,d]-w[b,c]\le w[a,d]-w[a,c]\) 即可满足。
也就是 \(w[a,c]+w[b,d]<w[a,d]+w[b,c]\),简记为交叉优于包含。
决策单调性可能会让人记录上一个点的决策位置然后暴力往后跳,但这样时间复杂度是错的,可能有一长串的位置都从 \(0\) 转移,还是 \(O(n^2)\)。
分治
如果 \(dp[i]=dp[j]+w[j,i]\) 中的 \(dp[j]\) 是上一轮的已经算出来的值,或者 \(dp[i]=w[j,i]\),那么就可以采用一种巧妙的分治做法。
每层我们找到 \(mid\),先把 \(mid\) 的答案和决策点算出来,然后分治到左右两边,限制决策点的左右区间。这样分治下去是 \(\log\) 层;每层因为决策点的左右限制,一层内决策点总的枚举次数是 \(O(n)\) 的,所以时间复杂度为 \(O(n\log n)\)。
例题 CF868F
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define cs const
#define in read()
inline int read(){
int p=0,f=1;char c=getchar();
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){p=p*10+c-48;c=getchar();}
return p*f;
}
cs int N=100005;
int n,K,a[N];
int dp[N][21],cnt[N],ans;
int TL,TR;
inline void add(int x){if(++cnt[x]^1)ans+=cnt[x]-1;}
inline void del(int x){if(--cnt[x])ans-=cnt[x];}
int calc(int L,int R){
while(TR<R)add(a[++TR]);
while(TL>L)add(a[TL--]);
while(TR>R)del(a[TR--]);
while(TL<L)del(a[++TL]);
return ans;
}
inline void solve(int l,int r,int Fl,int Fr,int k){
if(l>r)return ;
int mid=(l+r)>>1,fr=0;
for(int j=Fl;j<=Fr&&j<=mid;j++)
if(dp[j][k-1]+calc(j,mid)<dp[mid][k])
fr=j,dp[mid][k]=dp[j][k-1]+calc(j,mid);
solve(l,mid-1,Fl,fr,k);
solve(mid+1,r,fr,Fr,k);
}
signed main(){
n=in,K=in;
for(int i=1;i<=n;i++)a[i]=in;
for(int k=0;k<=K;k++)
for(int i=0;i<=n;i++)
dp[i][k]=1000000000000000000;
dp[0][0]=0;
for(int k=1;k<=K;k++)
solve(1,n,0,n-1,k);
cout<<dp[n][K];
return 0;
}
二分决策栈/队列
这个方法比 dp 可以先算中间后算前面这种需要满足特殊性质的分治做法更通用。
两者也有相似之处,都有维护一个最优决策点和其适用的区间。
具体来说,定义三元组 \((l,r,t)\) 表示现在 \([l,r]\) 的最优决策点为 \(t\)。
用一个单调队列来存三元组,保证 \(t\) 单增,对于 \(i\) 的转移,把队头 \(r<i\) 的三元组去掉,然后用队头的最优决策点更新。
对于 \(i\) 的插入,应该把 \((l_i,r_i,i)\) 插入队尾,考虑怎么找 \(l_i,r_i\)。
首先设 \(w(j,i)\) 表示从 \(j\) 转移到 \(i\) 的决策值,那么如果 \(w(i,n)\) 劣于 \(w(q[tl].t,n)\),\(i\) 就不需要插入决策栈了。
否则显然 \(r_i=n\),然后只要 \(w(q[tl].t,q[tl].l)\) 劣于 \(w(i,q[tl].l)\) 就说明整个 \([q[tl].l,q[tl].r]\) 区间的最优决策点都应变为 \(i\),弹出队尾。
直到 \(w(q[tl].t,q[tl].l)\) 优于 \(w(i,q[tl].l)\)。此时判断 \(w(q[tl].t,q[tl].r)\) 优于 \(w(i,q[tl].r)\) 那么 \(l_i\) 就确定了。否则 \(l_i\) 就在 \([q[tl].l,q[tl].r]\) 之间,用二分找到分段点,再把 \(q[tl]\) 的适用区间拆开即可。
时间复杂度 \(O(n\log n)\)。
例题 P1912
注意这题中间的 dp 值爆 long long,用 long double 最后强转为 long long。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define ll long double
#define cs const
#define in read()
inline int read(){
int p=0,f=1;
char c=getchar();
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){p=p*10+c-'0';c=getchar();}
return p*f;
}
cs int N=100005;
cs int inf=1000000000000000000;
int T,n,L,P;
inline ll qpow(ll a,int b){ll ans=1;for(;b;b>>=1,a*=a)if(b&1)ans*=a;return ans;}
ll dp[N];
int sum[N],fr[N];
string s[N];
struct decinode{
int l,r,t;
}a[N];
decinode q[N];
int qh,qt;
inline ll w(int j,int i){
return dp[j]+qpow(abs(sum[i]-sum[j]-1-L),P);
}
inline int bin(int L,int R,int t,int i){
int l=L,r=R,mid;
while(l<r){
mid=(l+r)>>1;
if(w(t,mid)>=w(i,mid))r=mid;
else l=mid+1;
}
return l;
}
inline void getans(int x){
if(x==0)return ;
getans(fr[x]),cout<<'\n';
for(int i=fr[x]+1;i<x;i++)
cout<<s[i]<<' ';
cout<<s[x];
}
signed main(){
T=in;
while(T--){
n=in,L=in,P=in;
for(int i=1;i<=n;i++)
cin>>s[i],sum[i]=sum[i-1]+s[i].length();
for(int i=1;i<=n;i++)sum[i]+=i;
q[qh=qt=1].l=1,q[1].r=n,q[1].t=0;
for(int i=1,j,l;i<=n;i++){
while(q[qh].r<i)qh++;
j=q[qh].t,dp[i]=w(j,i),fr[i]=j,l=n;
if(w(q[qt].t,n)>=w(i,n)){
while(qt>=qh&&w(q[qt].t,q[qt].l)>=w(i,q[qt].l))l=q[qt--].l;
if(qt>=qh&&w(q[qt].t,q[qt].r)>=w(i,q[qt].r))l=bin(q[qt].l,q[qt].r,q[qt].t,i);
if(q[qt].r>=l)q[qt].r=l-1;
q[++qt].l=l,q[qt].r=n,q[qt].t=i;
}
}
if(dp[n]>inf)cout<<"Too hard to arrange\n";
else cout<<(long long)dp[n],getans(n),cout<<'\n';
cout<<"--------------------\n";
}
return 0;
}
然后这里膜拜 FlashHu 巨佬,在洛谷诗人小G的题解区说明了数形结合的决策单调性理解。
具体来说,一个 \(dp[i]=\max/\min\{w[j,i]\}\),把 \(w[j,i]\) 看成每个 \(j\) 都有的一个关于 \(i\) 的函数。
比如 \(w[j,i]=a[j]+\sqrt{i-j}\),一部分 \(j\) 的函数图像为
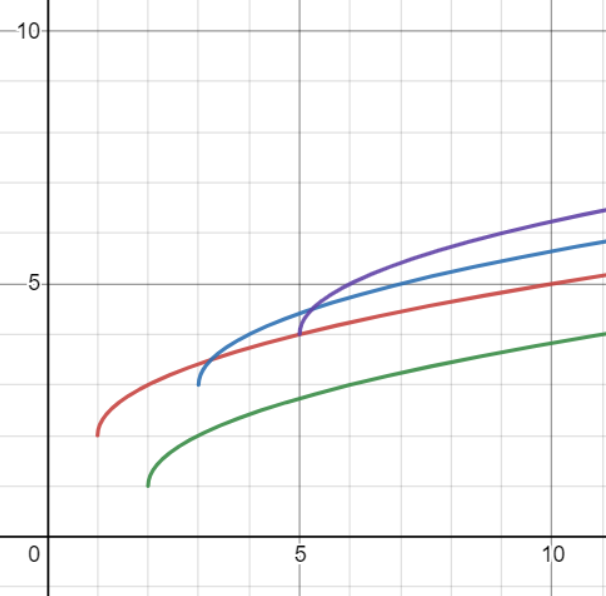
然后 \(dp[i]\) 就是要从这些函数图像在 \(i\) 点处的值中选择最大或最小值。
注意一个特性是 任意两个函数图像都满足最多只有 1 个交点。
因为两函数图像只有一个交点就意味着在交点之前是一个决策优,在交点之后是另一个决策更优。
还有一些满足函数单调性的转移,比如 \(w[j,i]=dp[j]+|sum[i]-sum[j]-C|^P\),满足 \(P\) 一定,\(i>j\) 且 \(sum[i]>sum[j]\)。由于有绝对值,那么对于每个 \(j\) 这就是一个关于 \(x=sum[j]+C\) 对称的类似二次函数一样的图形,由于 \(P\) 一定,这些图形的交点自然只会有 1 个了。
于是你就可以从四边形不等式之外,用数形结合的角度分析转移是否满足决策单调性了。


