半平面交
说起来简单但是写起来还是好麻烦。。。
首先半平面交是指给出多条向量和起点,规定只取向量的左侧或右侧,求最终得到的交。
我们只需要维护交的凸包上的直线和它们的交点。
可以 \(O(n^2)\) 地暴力,但甚至 \(O(n\log n)\) 还要好写点??
把所有点逆时针排序,最后的交就是所有直线左半平面的交。
首先把所有直线搞出来,用起点和向量表示
for(int i=1;i<=n;i++){
m=in;
for(int j=1;j<=m;j++)x[j]=in,y[j]=in;
for(int j=1;j<m;j++)a[++an]=Line({x[j],y[j]},{x[j+1]-x[j],y[j+1]-y[j]});
a[++an]=Line({x[m],y[m]},{x[1]-x[m],y[1]-y[m]});
}
我们的思路是按极角加入直线并维护一个凸包,这样会比杂乱无章的插入舒服很多,先把所有直线按向量极角排序。
排序时我们注意到,如果有两条直线极角相同,我们需要保留靠左的直线,这里不能只看横纵坐标,而应用叉乘正负判断。如果有两条线在同一直线,因为我们维护的是直线,所以可以任取。
struct vec{// point/vector
double x,y;
vec(){}
vec(double inx,double iny):x(inx),y(iny){}
vec operator+(cs vec a){return {x+a.x,y+a.y};}
vec operator-(cs vec a){return {x-a.x,y-a.y};}
vec operator*(cs double b){return {x*b,y*b};}
vec operator/(cs double b){return {x/b,y/b};}
}b[N];
double dotp(vec a,vec b){return a.x*b.x+a.y*b.y;}// dot product
double crsp(vec a,vec b){return a.x*b.y-a.y*b.x;}//cross product
struct Line{
vec s,e;//s->point,e->vector
double K;
Line(){}
Line(vec S,vec E):s(S),e(E),K(atan2(E.x,E.y)){}
bool operator<(cs Line a)//Keep the line near to left
{return (K-a.K>eps||K-a.K<-eps)?K>a.K:crsp(a.e,{s.x-a.s.x,s.y-a.s.y})>0;}
}a[N],q[N];
把直线排序之后就去重
sort(a+1,a+1+an);a[0].K=10000000000,m=0;
for(int i=1;i<=an;i++)
if(a[i].K-a[i-1].K<-eps)a[++m]=a[i];
接下来用一个双端队列维护凸包上的边,再维护它们的交点。
然后我们自己画画图,可以发现由于我们是按极角加边,所以一次加边对队尾的影响只有两种情况:
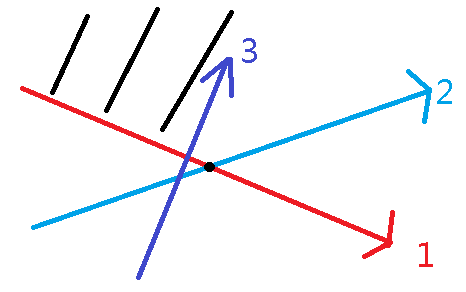
若是上一个交点在当前直线右边,那么上一条边就没有用了,应该去掉。
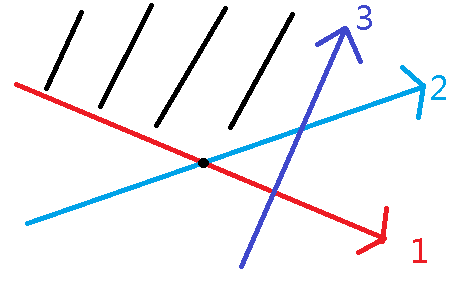
若是上一个交点在当前直线左边,那么上一条直线就应该保留。
同时我们注意到一条边还可能对队头的边产生影响,再画画图,我们同样注意到第一条直线的去留和第一个交点是否在当前直线左边有关
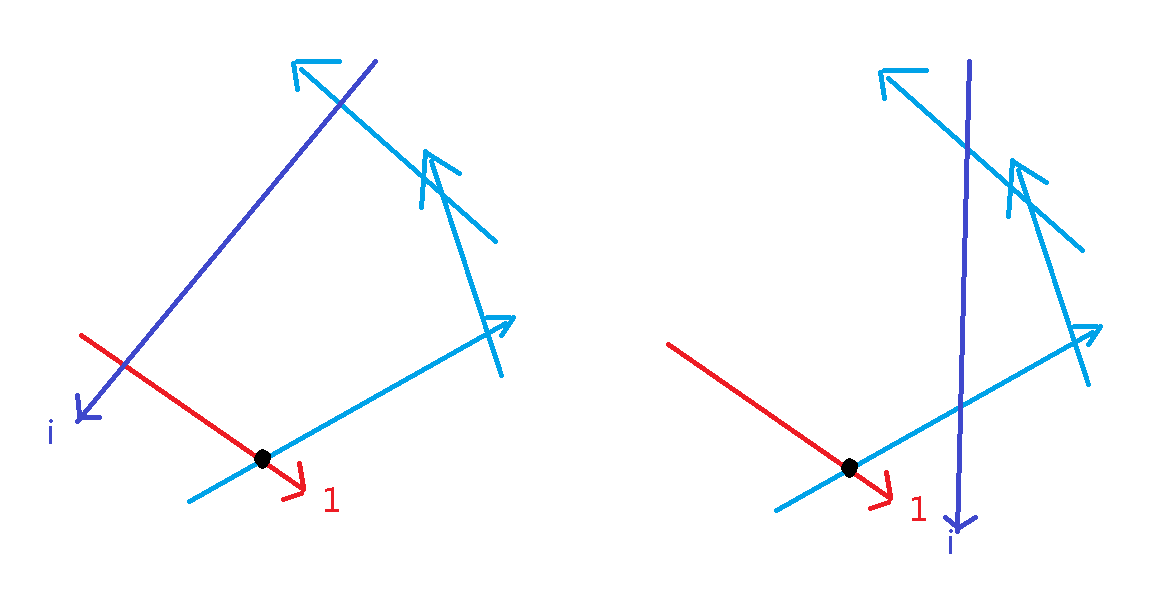
最后,因为我们一直是用新的直线来干掉队尾的直线,所以可能会出现队尾最后没有去干净的情况
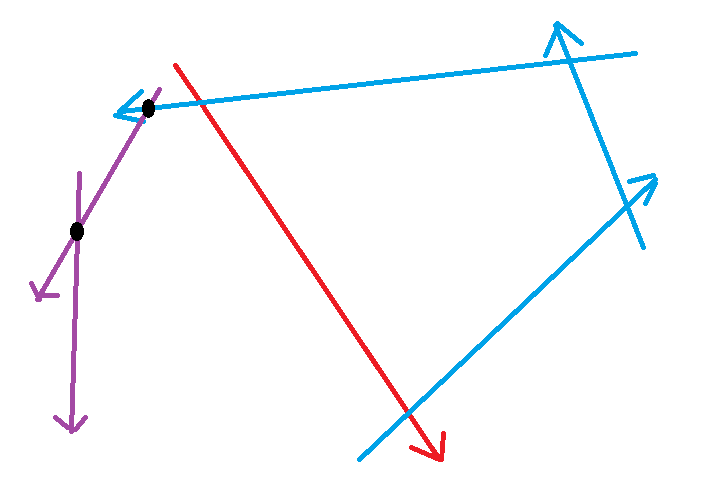
这种情况发现所有多余的边与上一条边的交点都在队头直线的右边。
所以维护凸包时,我们只需要,判断队尾,判断队首,加入直线,维护交点。
最后再把多余的直线干掉。
for(int i=1;i<=m;i++){
while(tl>hd&&rightof(b[tl],a[i]))tl--;
while(hd<tl&&rightof(b[hd+1],a[i]))hd++;
q[++tl]=a[i];
if(tl>hd)b[tl]=getcrspt(q[tl-1],q[tl]);
}
while(rightof(b[tl],q[hd]))tl--;
其中的求交点要小心竖直不存在斜率的直线
bool rightof(vec t,Line p){//if the point is on the right of the line
t.x-=p.s.x,t.y-=p.s.y;
if(crsp(p.e,t)<=0)return true;
return false;
}
vec getcrspt(Line x,Line y){//to get the cross point of two lines
if(abs(x.e.x)>abs(y.e.x))swap(x,y);
if(x.e.x<=eps&&x.e.x>=-eps){
double k2=y.e.y/y.e.x,b2=y.s.y-y.s.x*k2;
return {x.s.x,x.s.x*k2+b2};
}
double k1=x.e.y/x.e.x,b1=x.s.y-x.s.x*k1;
double k2=y.e.y/y.e.x,b2=y.s.y-y.s.x*k2;
return {(b2-b1)/(k1-k2),k1*(b2-b1)/(k1-k2)+b1};
}
好了,现在你得到了凸包上的 \(n\) 条直线和 \(n-1\) 个交点,并且由于我们是按极角排序加边,这些点都是排好序的,所以直接三角剖分算面积。(叉乘的几何意义是两向量夹的平行四边形面积)
vec t=getcrspt(q[hd],q[tl]);
for(int i=hd+1;i<=tl;i++)
b[i].x-=t.x,b[i].y-=t.y;
for(int i=hd+1;i<tl;i++)
ans+=crsp(b[i],b[i+1]);
cout<<fixed<<setprecision(3)<<ans/2;
ok,这样这道模板题就可以过了。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define cs const
#define in read()
inline int read(){
int p=0,f=1;
char c=getchar();
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){p=p*10+c-'0';c=getchar();}
return p*f;
}
cs double eps=1e-18;
cs double pi=acos(-1);
cs int N=505;
struct vec{// point/vector
double x,y;
vec(){}
vec(double inx,double iny):x(inx),y(iny){}
vec operator+(cs vec a){return {x+a.x,y+a.y};}
vec operator-(cs vec a){return {x-a.x,y-a.y};}
vec operator*(cs double b){return {x*b,y*b};}
vec operator/(cs double b){return {x/b,y/b};}
}b[N];
double dotp(vec a,vec b){return a.x*b.x+a.y*b.y;}// dot product
double crsp(vec a,vec b){return a.x*b.y-a.y*b.x;}//cross product
struct Line{
vec s,e;//s->point,e->vector
double K;
Line(){}
Line(vec S,vec E):s(S),e(E),K(atan2(E.x,E.y)){}
bool operator<(cs Line a)//Keep the line near to left
{return (K-a.K>eps||K-a.K<-eps)?K>a.K:crsp(a.e,{s.x-a.s.x,s.y-a.s.y})>0;}
}a[N],q[N];
int hd=1,tl;
int an,n,m;
double x[55],y[55],ans;
bool rightof(vec t,Line p){//if the point is on the right of the line
t.x-=p.s.x,t.y-=p.s.y;
if(crsp(p.e,t)<=0)return true;
return false;
}
vec getcrspt(Line x,Line y){//to get the cross point of two lines
if(abs(x.e.x)>abs(y.e.x))swap(x,y);
if(x.e.x<=eps&&x.e.x>=-eps){
double k2=y.e.y/y.e.x,b2=y.s.y-y.s.x*k2;
return {x.s.x,x.s.x*k2+b2};
}
double k1=x.e.y/x.e.x,b1=x.s.y-x.s.x*k1;
double k2=y.e.y/y.e.x,b2=y.s.y-y.s.x*k2;
return {(b2-b1)/(k1-k2),k1*(b2-b1)/(k1-k2)+b1};
}
signed main(){
n=in;
for(int i=1;i<=n;i++){
m=in;
for(int j=1;j<=m;j++)x[j]=in,y[j]=in;
for(int j=1;j<m;j++)a[++an]=Line({x[j],y[j]},{x[j+1]-x[j],y[j+1]-y[j]});
a[++an]=Line({x[m],y[m]},{x[1]-x[m],y[1]-y[m]});
}
sort(a+1,a+1+an);a[0].K=10000000000,m=0;
for(int i=1;i<=an;i++)
if(a[i].K-a[i-1].K<-eps)a[++m]=a[i];
for(int i=1;i<=m;i++){
while(tl>hd&&rightof(b[tl],a[i]))tl--;
while(hd<tl&&rightof(b[hd+1],a[i]))hd++;
q[++tl]=a[i];
if(tl>hd)b[tl]=getcrspt(q[tl-1],q[tl]);
}
while(rightof(b[tl],q[hd]))tl--;
vec t=getcrspt(q[hd],q[tl]);
for(int i=hd+1;i<=tl;i++)
b[i].x-=t.x,b[i].y-=t.y;
for(int i=hd+1;i<tl;i++)
ans+=crsp(b[i],b[i+1]);
cout<<fixed<<setprecision(3)<<ans/2;
return 0;
}

