wqs二分

wqs二分

wqs二分用来解决一类问题，该类问题一个突出的特征是答案具有凸性，（比如选某一类东西有贡献也有一定限制，求选 K 个该类物品时的最优解）并且这类问题一般在不要求选 K 个时能够较轻松地做出来。

首先要判断答案是否有凸性，我们可以发现比如最小生成树选 K 条的凸性就比较显然，每次多选一条必然选的是这些边里的最小值，并把原树上两点间最大值去掉，边权和变化是最小值减最大值，然后每次会把最大值和最小值去掉，所以斜率必然是单调的。然后最小生成树在没有限制时又有现成的做法，所以比较基础的wqs二分都是从最小生成树讲起。

我们来看看wqs二分的流程。

假设必须选 x 个时的答案是 g(x)，然后注意我们只知道 g(x) 的形状是个凸包，并不知道它实际的值。

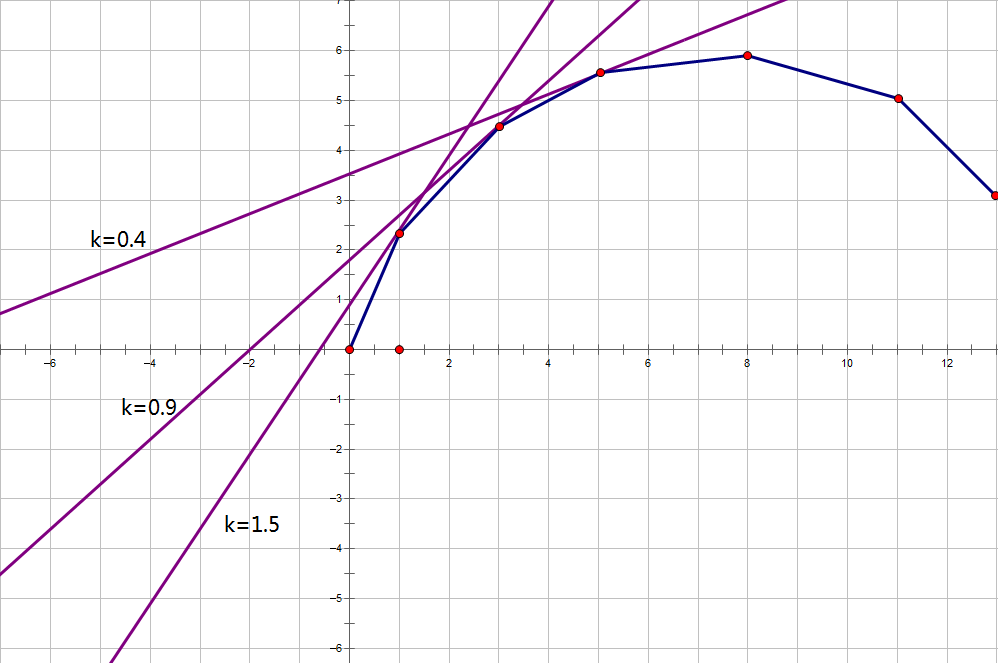
image

然后我们注意到一条斜率为 k 的可以对应到图像上的一个（或者一些）切点，此时设与图形相切的直线的截距为 f(x)。

于是我们二分斜率 k，得到一条直线，那么接下来如果我们能够快速求出直线与图形的切点位置，我们就可以根据得到的位置 x 与 K 的关系判断 k 接下来怎么二分。

在这个凸包里，我们发现直线截距 f(x) 最大时就对应了切点。

并且有 f(x)=g(x)−kx。g(x) 是选 x 个时的最优答案，g(x)−kx 就相当于把要选的一类物品全部减掉 k 后的选 x 个的答案。那么我们要让 f(x) 最大就是把要选的一类物品全部减掉 k 后没有限制的最优解，这样就可以做了。

我们注意到可能有一个区间的 k 都对应一个切点，所以我们最后二分出的 k 只会是两个端点之一。此时你的 k 可能对应到两个或者多个 x，所以我们只能利用已知 K 和斜率 k，截距 f(x) 算出答案 g(K)=f(x)+k×K。

讲的好意识还是来看题吧。

P5633 最小度限制生成树

P5633

给你一个有 n 个节点，m 条边的带权无向图，你需要求得一个生成树，使边权总和最小，且满足编号为 s 的节点正好连了 k 条边。

你发现这里跟 s 相连的边就是要选的一类物品，把它们叫做特殊边吧，所以我们二分 k，并把特殊边的边权加 k，然后直接跑最小生成树。

我们可以规定偏序先选特殊边，这样跑出来的就是边权一定时特殊边选的最多的，如果这样的特殊边边数还小于 K，那么斜率 k 就应该变小，否则 k 就应该保留并变大。

最后我们得到一个最优的斜率，并且由于我们刚刚定义的偏序我们用二分出来的 k 做一遍普通的生成树是特殊边选的最多的。那么我们怎么保证它能刚好选到 K 个呢？其实我们发现如果一个斜率对应几个点，那么这几个点一定是相邻的，而且从 x 到 x+1 其实相当于把权值相等的非特殊边换成了特殊边。这里我们二分时保证了此时的斜率是第一个特殊边数大于等于 K 的，所以我们一定可以在这些特殊边里轮换得到 K 条特殊边，且权值和不变。

所以最后直接返回 sum−mid×K 即可。

做这道题如果每次改特殊边的边权再全部排序时间会被卡，我们可以一开始把特殊边分出来，里面用类似归并排序的方式跑最小生成树。

然后这道题要注意一下判无解，首先判一下联通，然后如果选最多的特殊边都选不到 K 条，或者选最少的特殊边都超过了 K 条也是无解。

code

点击查看代码 
#include<bits/stdc++.h>
using namespace std;
#define int long long 
#define in read() 
inline int read(){
	int p=0,f=1;
	char c=getchar();
	while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
	while(isdigit(c)){p=p*10+c-'0';c=getchar();}
	return p*f;
}
const int N=5e4+5;
const int M=5e5+5;
int n,m,s,k;
struct Edge{
	int v,nxt;
}E[M<<1];
int head[N],en;
void insert(int u,int v){
	E[++en].v=v;
	E[en].nxt=head[u];
	head[u]=en;
}
int vis[N];
inline void dfs(int u){
	vis[u]=1;
	for(int i=head[u];i;i=E[i].nxt)
		if(!vis[E[i].v])dfs(E[i].v);
}
struct edge{
	int u,v,w;
	bool operator<(const edge x){
		return w<x.w;
	}
}e1[M],e2[M];
int e1n,e2n;
int fa[N];
inline int getf(int x){
	return fa[x]==x?x:fa[x]=getf(fa[x]);
}
inline bool merge(int x,int y){
	int f1=getf(x),f2=getf(y);
	if(f1==f2)return false;
	fa[f2]=f1;return true;
}
int flag,ans=0;
inline void solve(int mid,int &sum,int &res,int &ress){
	for(int i=1;i<=e2n;i++)e2[i].w+=mid;
	for(int i=1;i<=n;i++)fa[i]=i;
	int l=1,r=1;
	for(int i=1;i<=m;i++){
		if(res==n-1)break;
		if(r>e2n||(l<=e1n&&e1[l].w<e2[r].w)){
			if(merge(e1[l].u,e1[l].v))
				res++,sum+=e1[l].w;
			l++;
		}
		else{
			if(merge(e2[r].u,e2[r].v))
				res++,sum+=e2[r].w,ress++;
			r++;		
		}
	}
	for(int i=1;i<=e2n;i++)e2[i].w-=mid;
}
signed main(){
	n=in,m=in,s=in,k=in;
	for(int i=1,u,v;i<=m;i++){
		u=in,v=in;
		if(u==s||v==s)
			e2[++e2n].u=u,e2[e2n].v=v,e2[e2n].w=in,
			insert(u,v),insert(v,u);	
		else
			e1[++e1n].u=u,e1[e1n].v=v,e1[e1n].w=in,
			insert(u,v),insert(v,u);
	}
	dfs(1);
	for(int i=1;i<=n;i++)
		if(!vis[i])cout<<"Impossible",exit(0);
	sort(e2+1,e2+1+e2n),sort(e1+1,e1+1+e1n);
	int l=-30001,r=30001,mid,sum=0,res=0,ress=0;
	solve(r,sum,res,ress);
	if(ress>k)cout<<"Impossible",exit(0);
	sum=res=ress=0;
	solve(l,sum,res,ress);
	if(ress<k)cout<<"Impossible",exit(0);
	sum=res=ress=0;	
	while(l<r){
		mid=(l+r+1)>>1;
		solve(mid,sum,res,ress);
		if(ress>=k)l=mid;
		else if(ress<k)r=mid-1;
		sum=0,res=0,ress=0;
	}
	solve(l,sum,res,ress);
	cout<<sum-k*l;
	return 0;
}

CF125E MST Company

CF125E

这题是刚刚的加强版，要求输出方案，这下好像不好做了，我们又不知道它是怎么换的边。

那么有没有什么方法可以构造一组wqs二分的解呢，这是可行的。
汲取这篇里写的UOJ群里讨论的构造法。

首先我们注意到每组轮换的边的边权相等，所以我们可以把边权相同的分到一组里。

然后我们先跑一遍 k 最大和 k 最小的最小生成树，此时我们可以得到同一批次里至少要选的特殊边数和至多能选的特殊边数。

有了这些就好办了，我们在最后得到最优斜率跑最后一遍最小生成树时就可以开始构造方案了，首先把每一批里至少要选的特殊边数选了，然后依次选至多的特殊边，直到现在选了特殊边会超过 K，现在随便找几个填满就好了。

这种构造方式应该对其他大部分wqs二分的构造都适用，还是值得看一看。

虽然还没有实现

P2619 [国家集训队]Tree I

P2619
这是wqs在论文里提到的例题。

code

点击查看代码 
#include<bits/stdc++.h>
using namespace std;
#define int long long 
#define in read() 
inline int read(){
	int p=0,f=1;
	char c=getchar();
	while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
	while(isdigit(c)){p=p*10+c-'0';c=getchar();}
	return p*f;
}
const int N=5e4+5;
const int M=1e5+5;
int n,m,k;
struct edge{
	int u,v,w;
	bool operator<(const edge x){
		return w<x.w;
	}
}e1[M],e2[M];
int e1n,e2n;
int fa[N];
inline int getf(int x){
	return fa[x]==x?x:fa[x]=getf(fa[x]);
}
inline bool merge(int x,int y){
	int f1=getf(x),f2=getf(y);
	if(f1==f2)return false;
	fa[f2]=f1;return true;
}
int flag,ans=0;
inline void solve(int mid,int &sum,int &res,int &ress){
	for(int i=1;i<=e2n;i++)e2[i].w+=mid;
	for(int i=0;i<n;i++)fa[i]=i;
	int l=1,r=1;
	for(int i=1;i<=m;i++){
		if(res==n-1)break;
		if(r>e2n||(l<=e1n&&e1[l].w<e2[r].w)){
			if(merge(e1[l].u,e1[l].v))
				res++,sum+=e1[l].w;
			l++;
		}
		else{
			if(merge(e2[r].u,e2[r].v))
				res++,sum+=e2[r].w,ress++;
			r++;		
		}
	}
	for(int i=1;i<=e2n;i++)e2[i].w-=mid;
}
signed main(){
	n=in,m=in,k=in;
	for(int i=1,u,v,w,c;i<=m;i++){
		u=in,v=in,w=in,c=in;
		if(!c)e2[++e2n].u=u,e2[e2n].v=v,e2[e2n].w=w;	
		else e1[++e1n].u=u,e1[e1n].v=v,e1[e1n].w=w;
	}
	sort(e2+1,e2+1+e2n),sort(e1+1,e1+1+e1n);
	int l=-1000,r=1000,mid,sum=0,res=0,ress=0;
	while(l<r){
		mid=(l+r+1)>>1;
		solve(mid,sum,res,ress);
		if(ress>=k)l=mid;
		else if(ress<k)r=mid-1;
		sum=0,res=0,ress=0;
	}
	solve(l,sum,res,ress);
	cout<<sum-k*l;
	return 0;
}

需要注意的是，wqs二分其实属于一种利用题目凸性的凸优化。比起最小生成树更常见的，你可以在很多 dp 中用到它，此时要看出 dp 的决策凸性就不是一件简单的事了。所以给几道题自己做做吧。

P1484 种树
突然注意到一些题斜率应该二分到小数。

点击查看代码 
#include<bits/stdc++.h>
using namespace std;
#define int long long 
#define in read() 
inline int read(){
	int p=0,f=1;
	char c=getchar();
	while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
	while(isdigit(c)){p=p*10+c-'0';c=getchar();}
	return p*f;
}
const double eps=1e-1;
const int N=5e5+5;
int n,K;
double a[N]; 
double dp[N][2],tans;
int num[N][2],tnum;
void solve(double mid){
	for(int i=1;i<=n;i++)a[i]-=mid;
	for(int i=0;i<=n;i++){
		if(dp[i][1]>=dp[i][0])
			dp[i+1][0]=dp[i][1],num[i+1][0]=num[i][1];
		else dp[i+1][0]=dp[i][0],num[i+1][0]=num[i][0];
		dp[i+1][1]=dp[i][0]+a[i];
		num[i+1][1]=num[i][0]+(i!=0);
	}
	for(int i=1;i<=n;i++)a[i]+=mid;
	if(dp[n+1][0]>dp[n+1][1])tnum=num[n+1][0],tans=dp[n+1][0]+mid*tnum;
	else tnum=num[n+1][1],tans=dp[n+1][1]+mid*tnum;
}
signed main(){
	n=in,K=in;
	for(int i=1;i<=n;i++)a[i]=in;
	solve(0);
	if(tnum<=K)cout<<(int)tans,exit(0);
	double l=-1000000,r=1000000,mid;
	while(eps<r-l){
		mid=(l+r)/2;
		solve(mid);
		if(tnum<=K)r=mid;
		else l=mid+1;
	}
	solve(l);
	cout<<(int)(tans-(tnum-K)*l);
	return 0;
}

CF739E Gosha is hunting

CF802O April Fools' Problem (hard)

P4983 忘情

P4383 [八省联考 2018] 林克卡特树

其他优质博客

关于WQS二分算法以及其一个细节证明

Wqs二分

posted @   llmmkk  阅读(265)  评论(1)  编辑  收藏  举报
相关博文：
·  2022寒假刷题计划（1）
·  CSPS2022 题解
·  wqs 二分
·  wqs 二分
·  【9.30】wqs二分
阅读排行：
· 地球OL攻略 —— 某应届生求职总结
· 周边上新：园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源！
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】
点击右上角即可分享
微信分享提示
SQL AI 助手

目录导航