后缀数组
后缀数组
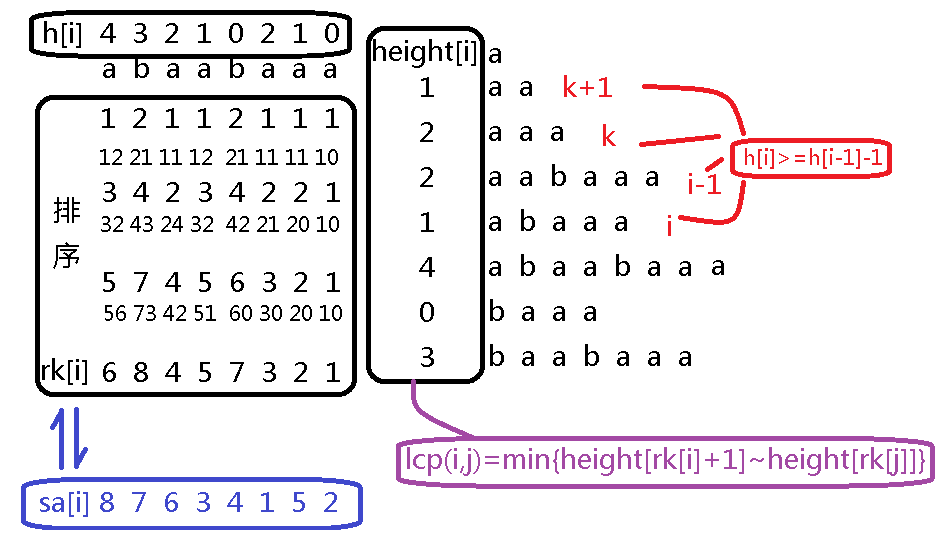
后缀排序
对于一个字符串 \(S\),将它的所有后缀按字典序从小到大排序,没有字符的位置默认字典序最小。如上图右侧就是排序后的后缀。
我们把 \(S_{i\sim n}\) 叫做 \(S\) 的第 \(i\) 个后缀。
数组
\(rk[i]\) 是 \(S\) 的第 \(i\) 个后缀在排序后的排名。
\(sa[i]\) 是排名为 \(i\) 的后缀在原字符串上的位置。显然有\(rk[sa[i]]=sa[rk[i]]=i\)。
\(height[i]\) 是排序后的后缀中排名为 \(i\) 与排名为 \(i-1\) 的两个后缀的lcp长度。lcp即最长公共前缀(longest common prefix)。
\(h[i]\) 是用来求 \(height\) 时的辅助数组,实际上并不需要用到;是第 \(i\) 个后缀与排序后排名在 \(i\) 的排名前一个的某字符串 \(k\) 两个后缀的LCP长度。即 \(h[i]=height[rk[i]]\)。
排序
为了将字符串的每个后缀排序,我们选择一种巧妙的 \(O(n\log n)\) 的方法,只需要从把每个位置往后 \(2^{k}\) 的这些字符串排序,下一次 \(k+1\),只需要用当前位置 \(i\) 合并上 \(i+2^{k}\) 的位置,以两个关键字来排序,如上图展示。
在用这两个关键字排序时,我们可以参考基数排序。
(部分转自 oi-wiki)
基数排序
基数排序是一种排序的思想,它将需要排序的元素分成 \(k\) 个关键字。按关键字的先后顺序从后往前对每一个关键字进行一次稳定的排序,从而做到对整个元素排序。
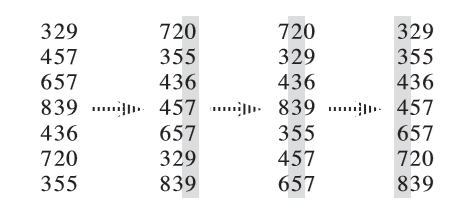
基数排序内部需要一种稳定的排序算法。
通常情况下,如果关键字的值域 \(w\) 较小,内部可以采用计数排序,时间复杂度为 \(O(k(n+w))\)。如果关键字的值域较大,就可以直接用快速排序,时间复杂度为 \(O(k n \log n)\)。
计数排序
计数排序是一种稳定的线性排序算法。若元素值域为 \(w\),那么计数排序的时间复杂度为 \(O(n+w)\)。
计数排序需要借助一个辅助的桶数组。
- 计算每个数的出现次数。
- 计算每个数出现次数的前缀和。
- 根据前缀和得到这个数的排名。
伪代码:

排序部分代码
inline void jsort(){//基数+计数排序
for(int i=0;i<=n;i++)cnt[i]=0;
for(int i=1;i<=n;i++)cnt[st[i].se]++;
for(int i=1;i<=n;i++)cnt[i]+=cnt[i-1];
for(int i=n;i>0;i--)tmp[cnt[st[i].se]]=st[i],cnt[st[i].se]--;
for(int i=0;i<=n;i++)cnt[i]=0;
for(int i=1;i<=n;i++)cnt[tmp[i].fi]++;
for(int i=1;i<=n;i++)cnt[i]+=cnt[i-1];
for(int i=n;i>0;i--)st[cnt[tmp[i].fi]]=tmp[i],cnt[tmp[i].fi]--;
}
且我们可以发现若某刻所有后缀的第一关键字都已不同,就没有再基数排序下去的意义了。
SA的应用
我们可以通过 \(height\) 做到快速求出 \(S\) 任意两后缀的LCP。
假设 \(rk[i]<rk[j]\),观察发现 \(LCP(i,j)=\min\{height[rk[i]+1]\sim height[rk[j]]\}\)。
可以使用 ST 表做到 \(O(n\log n)\) 预处理 \(O(1)\) 查询。
如何求出 \(height\)?
-
顺序暴力,\(O(n^2)\),×
-
利用 \(S\) 和后缀排序的性质,压缩复杂度做到 \(O(n)\),√
看到 \(h\) 数组,我们有 \(h[i]>=h[i-1]-1\)。
证明:
设 \(k\) 是排在 \(i-1\) 前一名的后缀,则它们的最长公共前缀是 \(h[i-1]\)。那么 \(k+1\) 将排在 \(i\) 的前面,并且 \(k+1\) 和 \(i\) 的最长公共前缀是 \(h[i-1]-1\)(这是因为排序是按字典序排序,\(k+1\) 和 \(i\) 相当于 \(k\) 和 \(i-1\) 各自去掉开头的一个字符,二者字典序大小顺序不变,LCP 减去开头的字符)。
我们又可以由 \(height\) 求 LCP 的方法得知 \(i\) 和它排名前一位的 LCP 至少是 \(h[i-1]-1\),即 \(h[i]\ge h[i-1]-1\)。
于是按照 \(h[1],h[2],\cdots ,h[n]\) 的顺序计算 \(height\) 时间复杂度可以降为 \(O(n)\)。并且我们只使用到了 \(h\) 的顺序,并不需要把真正的 \(h\) 求出来。
代码
#include<bits/stdc++.h>
using namespace std;
bool ss;
#define in read()
inline int read(){
int p=0,f=1;
char c=getchar();
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){p=p*10+c-'0';c=getchar();}
return p*f;
}
const int N=1e6+5;
string S;
int n,m,rk[N<<1],sa[N],ht[N];
struct llmmkk{
int fi,se,ref;
}st[N<<1],tmp[N<<1];
int cnt[N];
inline void jsort(){
for(int i=0;i<=n;i++)cnt[i]=0;
for(int i=1;i<=n;i++)cnt[st[i].se]++;
for(int i=1;i<=n;i++)cnt[i]+=cnt[i-1];
for(int i=n;i>0;i--)tmp[cnt[st[i].se]]=st[i],cnt[st[i].se]--;
for(int i=0;i<=n;i++)cnt[i]=0;
for(int i=1;i<=n;i++)cnt[tmp[i].fi]++;
for(int i=1;i<=n;i++)cnt[i]+=cnt[i-1];
for(int i=n;i>0;i--)st[cnt[tmp[i].fi]]=tmp[i],cnt[tmp[i].fi]--;
}
int ston[257];
int lg2[N],minn[N][21];
inline void SA(){
for(int i=0;i<n;i++)ston[S[i]]+=(!ston[S[i]]);
for(int i=1;i<=256;i++)ston[i]+=ston[i-1];
for(int i=1;i<=n;i++)rk[i]=ston[S[i-1]];
for(int k=1,t;k<=(n<<1);k<<=1){
for(int i=1;i<=n;i++)
st[i].fi=rk[i],
st[i].se=rk[i+k],
st[i].ref=i;
jsort();t=0;
for(int i=1;i<=n;i++){
if((st[i].fi^st[i-1].fi)||(st[i].se^st[i-1].se))t++;
rk[st[i].ref]=t;
}if(t==n)break;
}
for(int i=1;i<=n;i++)sa[rk[i]]=i;
for(int i=1;i<=n;i++){
ht[rk[i]]=max(ht[rk[i-1]]-1,0);
while(S[sa[rk[i]-1]+ht[rk[i]]-1]==S[i+ht[rk[i]]-1])
ht[rk[i]]++;
}
for(int i=2;i<=n;i++)lg2[i]=lg2[i/2]+1;
for(int i=1;i<=n;i++)minn[i][0]=ht[i];
for(int i=1;i<=20;i++)for(int j=1;j+(1<<(i-1))<=n;j++)
minn[j][i]=min(minn[j][i-1],minn[j+(1<<(i-1))][i-1]);
}
inline int getmin(int x,int y){
int t=lg2[y-x+1];
return min(minn[x][t],minn[y-(1<<t)+1][t]);
}
signed main(){
cin>>S;n=S.length();SA();
for(int i=1;i<=n;i++)cout<<sa[i]<<' ';
return 0;
}
例题
好啦,现在你已经学完后缀数组了,来试着解决几道简单的例题吧。



