Z-algorithm & kmp & 循环节

Z-algorithm 与循环节

[NOIP2020] 字符串匹配 中用到了Z算法求某个前缀的最长循环次数，大概是这样：

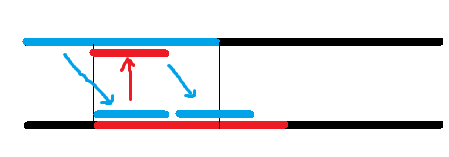
原 \(S\) 串上红蓝段匹配，为看清楚分开画。
上图中上面左边一段和下面的两段是循环节。

然后最后的结果是
\(S_{1\sim i}\) 这个前缀的循环次数是 \(\lfloor\frac{z[i+1]}{(i+1)}\rfloor+1\) 后面的 \(1\) 是开头这一段，\(\lfloor\frac{z[i+1]}{(i+1)}\rfloor\) 就是通过 Z 算法得到的后面的循环次数。

---

kmp 与循环节

这也让我想起曾经刚学 kmp 时做过和循环节有关的题，于是我去回忆了下kmp的循环节。

定理

假设 \(S\) 长为 \(n\),则 \(S\) 存在一个最小的从头开始的循环节，循环节长度为 \(n-next[n]\)。
若 \(n-next[n]\not\mid n\)，则 \(S\) 的最后一个周期不完整，需要补齐。

大概是：

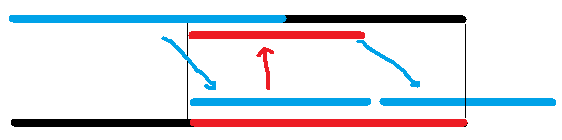
原 \(S\) 串上红蓝段匹配，为看清楚分开画。
上图中上面左边一段和下面的两段是循环节，最后一段循环节不完整。

---