线段树优化建图

在一类问题中，我们会使用时间复杂度和边数有关的算法，如【HNOI2019】校园旅行中的暴力算法，\(O(n+m)\) 的 Dijkstra，\(O(n+m)\) 的 tarjan 等，此时可能会由于边数太大而导致算法复杂度过大，此时的一个优化方向就是减少边数的规模，比如[【HNOI2019】校园旅行]中，我们充分利用题目条件的性质，将边分类然后只保留连通块的一颗生成树或基环树，将边数降至 \(n\)。而另一种常见的减少边规模的技巧就是线段树优化建图。

线段树优化建图

线段树优化建图的适用范围是连边和区间有关，比如一个区间内的点都向某个点连边，一个点向一个区间内的所有点连边，甚至一个区间内每个点向一个区间内每个点连边，这些边的规模是 \(n^2\) 的情况使用线段树优化建图之后边的规模就是 \(n\log n\) 了。

区间向点连边

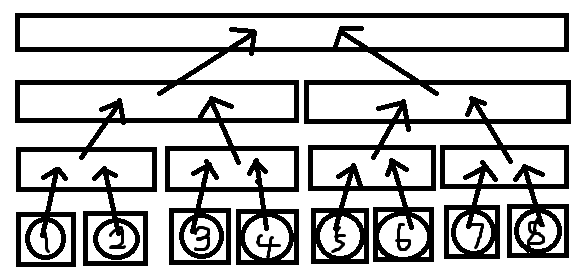
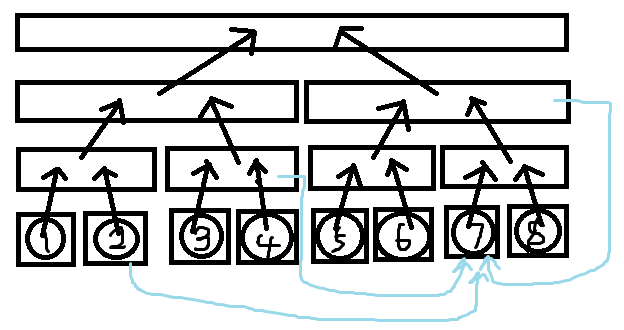
建出这样的图，然后区间向点连边只需要像正常线段树操作找到 \(\log\) 个区间再连就可以了，如区间 \([2,8]\) 连向 \(7\)：

点向区间连边

发现上面的图并不能适用，我们需要将边反向，

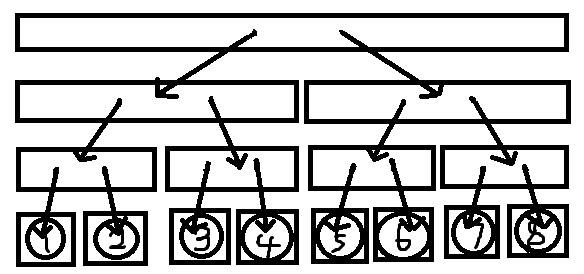
然后如果是 \(7\) 连向区间 \([2,8]\)，就会是

---

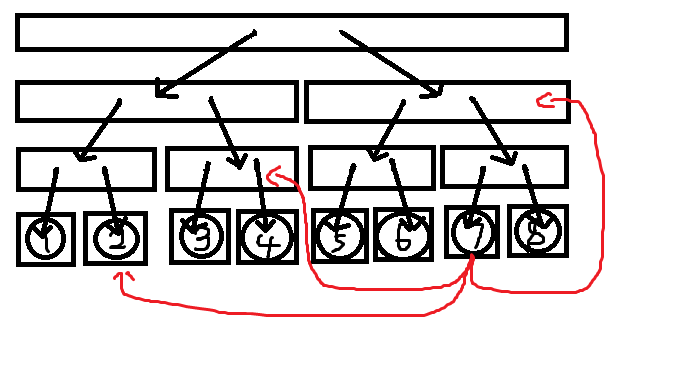
区间向区间连边

于是我们发现需要两颗线段树，并且叶子结点是共用的，所以我们可以把第二张图转一下，建出这样的图：

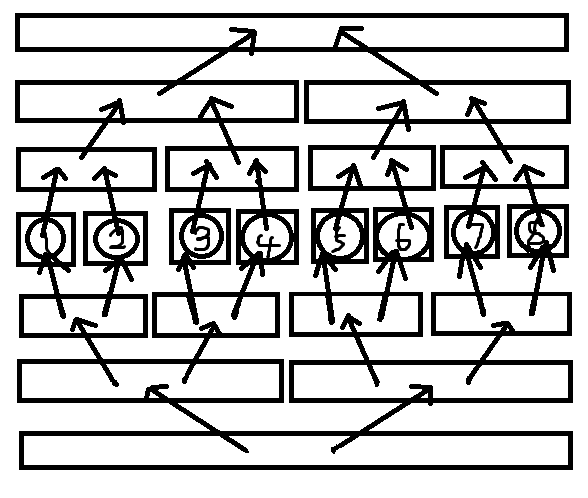
这张图就可以支持点向区间以及区间向点的操作，但如果有区间连区间呢？比如有三个操作，\(\color{red}{1\rightarrow[3,6]}\)，\(\color{blue}{[7,8]\rightarrow 2}\)，\(\color{gold}{[3,6]\rightarrow [7,8]}\)，然后连出来就是

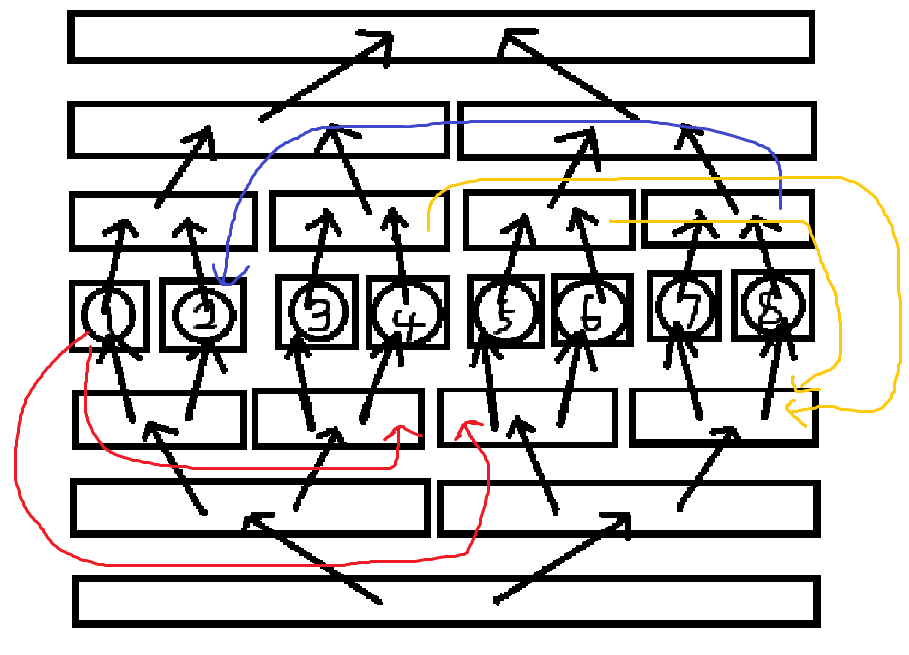
发现如果出现区间向区间连边的情况，如果直接连边，边的规模会变到 \(n\log^2n\)。

这样看起来就像没有线段树优化的直接建图一样，并不优，所以对于区间向区间连边的情况，我们再采取一个措施，就是建一个虚点，将涉及到的区间向虚点连边而不是直接连向区间，这样每新建一个虚点，边数增加就也是 \(\log\) 的了。那么就是：

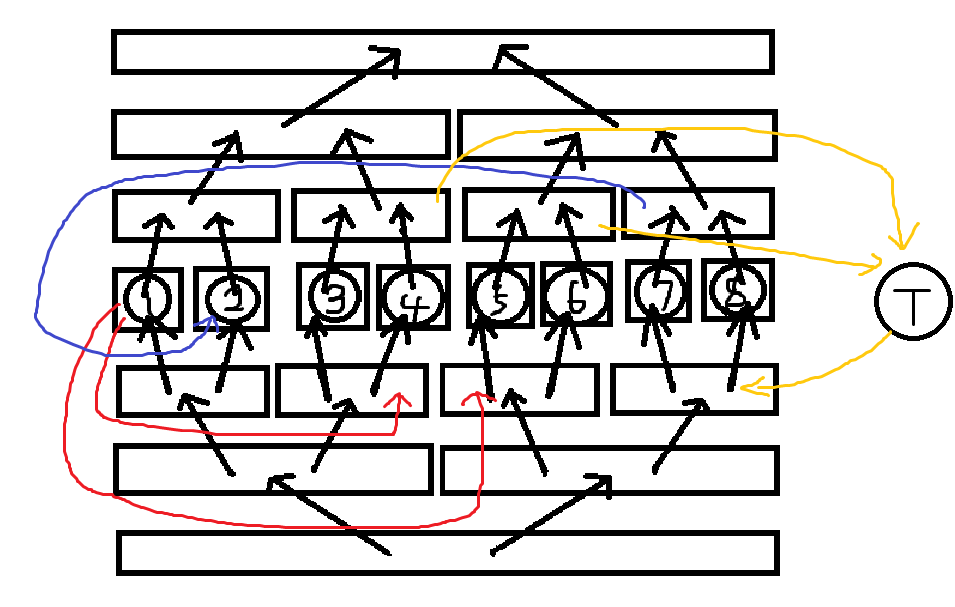
这样，我们发现边的规模就可以减少到 \(n\log n\)，但一个点到另一个点经过的边数增多了，所以如果图要求有边权，线段树上的边权都应该设为 \(0\)。

---