平面图最小割与对偶图最短路

平面图

平面图就是所有边都不相交的图，如

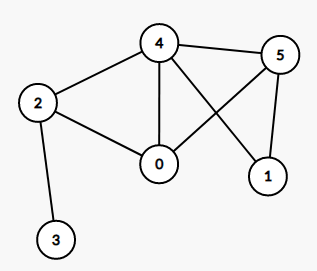
看起来相交了，但实际上没有相交，和下图等价，就是一个平面图

---

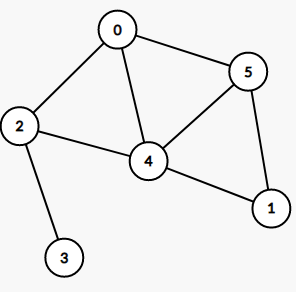
对偶图

对偶图是伴随平面图的一张图，

具体来说就是把原来平面图里的每个面当做一个节点

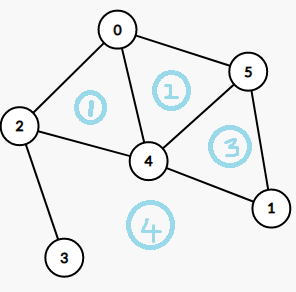
这些节点之间的边是和原图的边相交的，对偶图边权值等于原平面图边的权值

具体地：
设平面图为 $G$，对偶图为 $G'$，对于原图中每条边 $e$，

1. 若 $e$ 属于两个平面 $f1,f2$，则在对偶图中连边 $(f1',f2')$
2. 若 $e$ 属于一个平面 $f1$，则在对偶图中连自环 $(f1',f1')$

如：

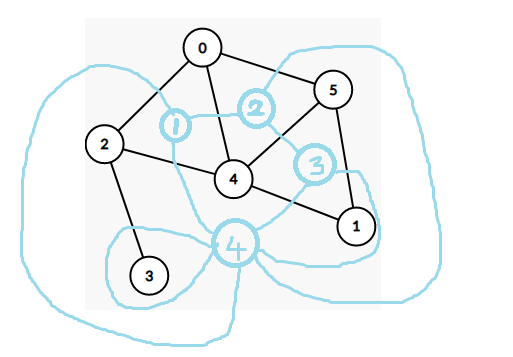
如果单独把对偶图抽出来就是：

---

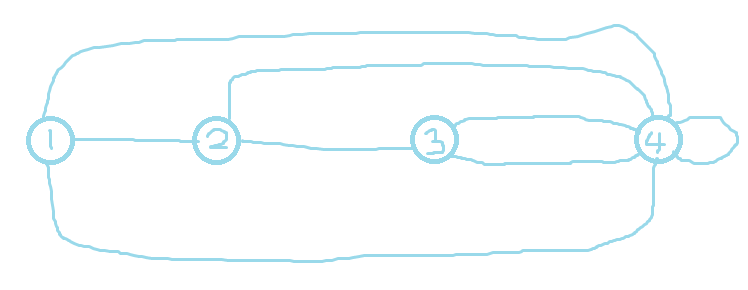
平面图最小割与对偶图最短路

在一类问题中我们常常会遇到网格图，并需要使用最小割算法，如[NOI2010] 海拔，[ICPC-Beijing 2006]狼抓兔子以及[CSP-S 2021] 交通规划，这些题的节点数可能非常多，导致 Dinic 太慢过不去，然后网格图正是一张典型的平面图，所以可以把平面图最小割转换成对偶图最短路。

可以看国集论文“周冬《两极相通——浅析最大—最小定理在信息学竞赛中的应用》”。

也就是说，平面图的最小割就是对偶图的最短路，所以我们在平面图上使用做最小割时，可以先构造出原图的对偶图，然后跑最短路即可，这样显然会比网络流快。

对于对偶图上的起点和终点，假如有这样一张网格图：

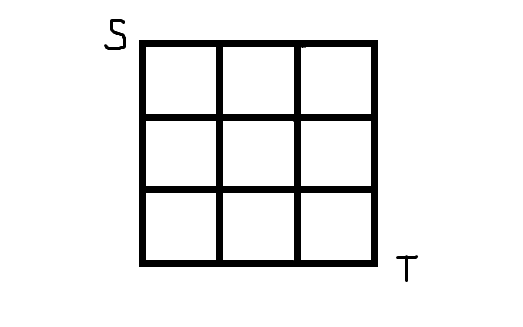
显然它的最小割一定是上下，上左，左右，左下这几种情况，也就是这样四种

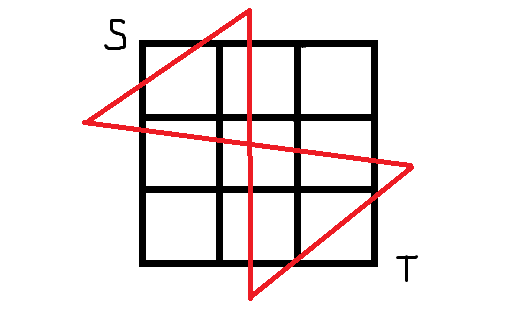
所以我们就可以把最外面的平面当成两个，上和右当做起点点，左和下当做终点，

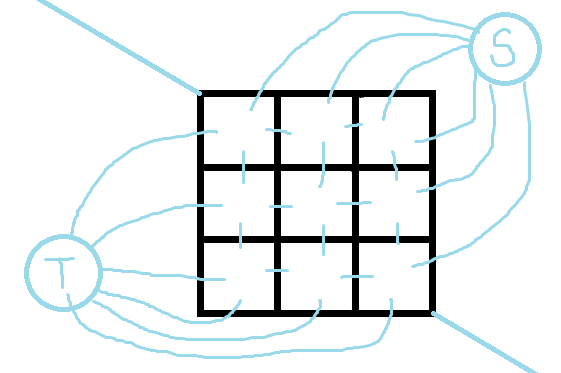
就可以建出这样的对偶图。

然后在实际的题目中会有一些方向的问题，可以自己画画对偶图找找规律啥的。

---

实际技巧

这里存一个网格图建对偶图的有用的东西，

规定这样记对偶图的点

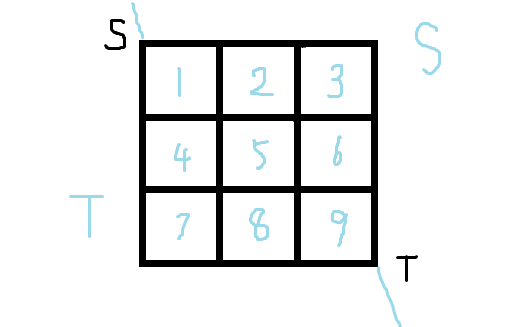
这样记平面图的横边

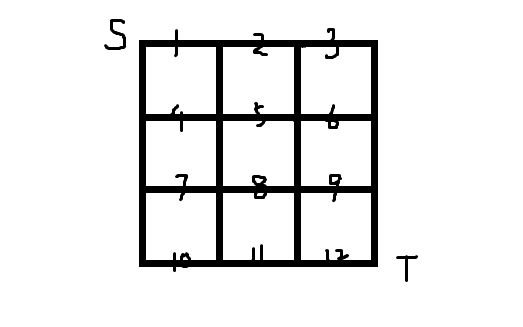
这样记平面图的竖边

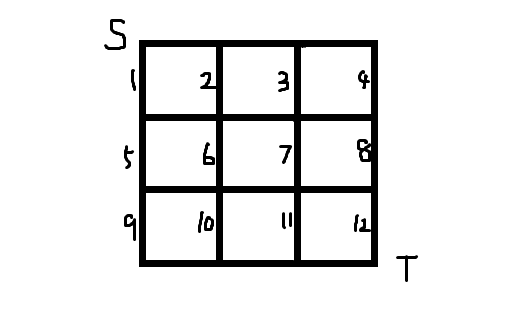
其实就是首先从上到下，其次从左到右编号，

给出一张 $n*m$ 的平面图，

那么可以这样找平面图的边在对偶图中对应的 $(u,v)$

inline int up(int i){
	if(i<=m)return s;
	return i-m;
}
inline int down(int i){
	if(i>n*m)return t;
	return i;
}
inline int left(int i){
	if(i%(m+1)==1)return t;
	return i-(i-1)/(m+1)-1;
}
inline int right(int i){
	if(i%(m+1)==0)return s;
	return i-i/(m+1);
}

up 和 down 用来找平面图横边，left 和 rignt 用来找平面图竖边。

边的方向问题：

原平面图中从 $S$ 流向 $T$ 的边，在对偶图中也从 $S$ 流向 $T$，具体可以参考 海拔 的代码。

海拔的编号方法就是上面的方法。

---