[ZJOI2013]K大数查询 (整体二分理解)
链接:
题意:
维护 \(n(1\leq n\leq 5\times10^4)\) 个可重整数集,编号从 \(1\) 到 \(n\)。有 \(m(1\leq m\leq5\times10^4)\) 个操作:
1 l r c表示将 \(c\) 插入到编号在 \([l,r]\) 的集合中。2 l r c表示查询编号在 \([l,r]\) 的集合的并集中的第 \(c\) 大数。
分析:
这道题除了用树套树等方法外,还可以用整体二分。
参考《浅谈数据结构题的几个非经典解法》的介绍:
所谓整体二分,需要数据结构题满足以下性质:
- 询问的答案具有可二分性
- 修改对判定答案的贡献相对独立,修改之间互不影响效果
- 修改如果对判定答案有贡献,则贡献为一确定的与判定标准无关的值
- 贡献满足交换律,结合律,具有可加性
- 题目允许离线操作
询问的答案有可二分性质显然是前提,我们发现,因为修改对判定标准的贡献相对独立,且贡献的值(如果有的话)与判定标准无关,所以如果我们已经计算过某一些修改对询问的贡献,那么这个贡献永远不会改变,我们没有必要当判定标准改变时再次计算这部分修改的贡献,只要记录下当前的总贡献,再进一步二分时,直接加上新的贡献即可。
这样的话,我们发现,处理的复杂度可以不再与序列总长度直接相关了,而可能只与当前待处理序列的长度相关
简而言之:答案本身可以二分,修改之间互不影响,每个修改对每个查询的贡献不变,贡献可以直接加减,允许离线。
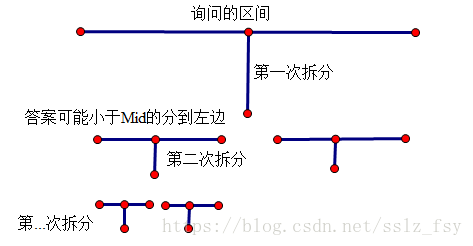
以及FSYo巨巨的图:
回到这道题上:
首先考虑普通二分:对每个查询考虑在它前面的所有修改,二分答案并将大于答案的修改在线段树上区间加一,再看查询的区间有多少大于答案的数,时间复杂度为 \(O(n\log n+m^2\log n)\)。将 \(n,m\) 视为同阶就是 \(O(n^2\log n)\)。这样对于每个查询分别二分会很慢,整体二分就可以把所有查询一次性解决。
具体操作是这样的,首先把所有修改和查询拉到一条序列上,维护这条当前序列在数组上的范围 \([l,r]\) 和答案范围 \([ansl,ansr]\),在本题中分别为 \(1,m,-n,n\)。然后要将这条序列分成两部分,但不是对半分,和普通二分类似的操作:首先令 \(mid=(ansl+ansr)/2\),从左往右扫,对每个扫到的修改,如果大于 \(mid\),那就在线段树上区间加一,并将这个修改放到左部分;如果小于等于 \(mid\),就把修改放到右部分。对每个扫到的询问,看查询区间有多少大于 \(mid\) 的数,如果数量小了,说明 \(mid\) 过大,所以把询问放到左边;如果数量大了,说明 \(mid\) 小了,我们减去查询到的数(意味着左边的贡献全部接受),然后把询问放到右边。然后左右两部分分治下去,每次把线段树清空。
感性理解一下,放到左边的查询是答案大了要减小,放到右边的查询是答案小了要增大,所以右边的查询不仅要减去左边的修改的贡献,还要在右边选择其他修改的贡献,而左边的查询则需要在左边的贡献中再选择。
整体二分把所有询问一次性同时解决了,时间复杂度降为了 \(O(n\log^2 n)\),非常的强大。
代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define in read()
inline int read(){
int p=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){p=p*10+c-'0';c=getchar();}
return p*f;
}
const int N=1e5+5;
int n,m;
struct ques{
int opt,l,r,c,o;
}q[N],tl[N],tr[N];
int sum[N<<2],tag[N<<2],cov[N<<2];
inline void pushup(int p){sum[p]=sum[p<<1]+sum[p<<1|1];}
inline void f(int l,int r,int p,int d){
sum[p]+=(r-l+1)*d;
tag[p]+=d;
}
inline void cf(int p){sum[p]=tag[p]=0;cov[p]=1;}
inline void pushdown(int l,int r,int p){
if(cov[p]){
cf(p<<1);
cf(p<<1|1);
cov[p]=0;
}
if(tag[p]){
int mid=(l+r)>>1;
f(l,mid,p<<1,tag[p]);
f(mid+1,r,p<<1|1,tag[p]);
tag[p]=0;
}
}
inline void change(int l,int r,int p,int cl,int cr,int d){
if(l>=cl&&r<=cr){f(l,r,p,d);return ;}
pushdown(l,r,p);
int mid=(l+r)>>1;
if(cl<=mid)change(l,mid,p<<1,cl,cr,d);
if(cr>mid)change(mid+1,r,p<<1|1,cl,cr,d);
pushup(p);
}
inline int query(int l,int r,int p,int ql,int qr){
if(l>=ql&&r<=qr)return sum[p];
pushdown(l,r,p);
int mid=(l+r)>>1,res=0;
if(ql<=mid)res+=query(l,mid,p<<1,ql,qr);
if(qr>mid)res+=query(mid+1,r,p<<1|1,ql,qr);
return res;
}
int vis[N];
int ans[N];
inline void solve(int l,int r,int ansl,int ansr){
if(l>r)return ;
if(ansl==ansr){
for(int i=l;i<=r;i++)
if(q[i].opt==2)ans[q[i].o]=ansl;
return ;
}
bool bl=false,br=false;cf(1);
int ll=0,rr=0,mid=(ansl+ansr)>>1;
for(int i=l;i<=r;i++){
if(q[i].opt==1){
if(q[i].c>mid){
change(1,n,1,q[i].l,q[i].r,1);
tr[++rr]=q[i];
}
else tl[++ll]=q[i];
}
else{
int t=query(1,n,1,q[i].l,q[i].r);
if(t>=q[i].c)
tr[++rr]=q[i],br=true;
else{
q[i].c-=t;
tl[++ll]=q[i],bl=true;
}
}
}
for(int i=1;i<=ll;i++)q[l+i-1]=tl[i];
for(int i=ll+1;i<=ll+rr;i++)q[l+i-1]=tr[i-ll];
if(bl)solve(l,l+ll-1,ansl,mid);
if(br)solve(l+ll,r,mid+1,ansr);
}
int qn;
signed main(){
n=in,m=in;
for(int i=1;i<=m;i++)
q[i].opt=in,q[i].l=in,q[i].r=in,q[i].c=in,q[i].o=(q[i].opt==2)?++qn:0;
solve(1,m,-n,n);
for(int i=1;i<=qn;i++)
cout<<ans[i]<<'\n';
return 0;
}
例题推荐: