点分治
点分治:
前言:
我太菜了。
用途:
点分治用于静态树上统计路径一类的问题。
如查询边带边权的树上是否存在长度为 \(k\) 的点对等。
算法:
由于只有统计路径的操作,所以这棵树的根是任意取的,先假设树根为1。
那么对于所有路径,只有
- 经过树根。(图中红色)
- 不经过树根。(图中蓝色)
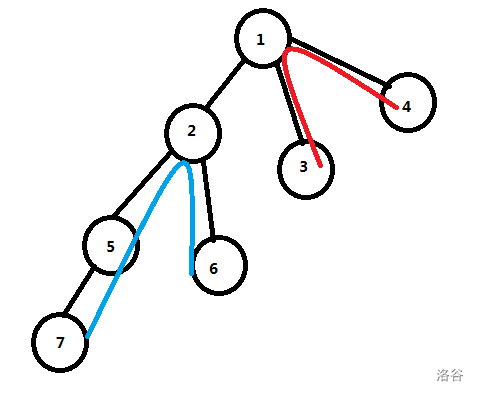
对于情况1,我们当然可以从根遍历整棵树,从而根据每个节点到根的距离等数据得出1的答案。
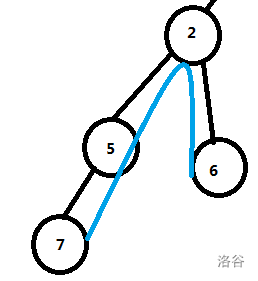
对于情况2,发现不经过树根的路径必然在根节点的某一棵子树内,所以可以递归树根的每一棵子树,即可将情况2转化为情况1,如下图。在递归中就只需处理情况1了。
所以点分治算法只需要每次从根出发,统计这棵树的数据,得到经过树根的答案,再递归每棵子树。选取根(点),递归子树(分治)也就是点分治了。
那么点分治的时间复杂度呢?
发现每层递归中都会遍历所有节点,所以复杂度是和递归层数相关的。
对于这样一条链。
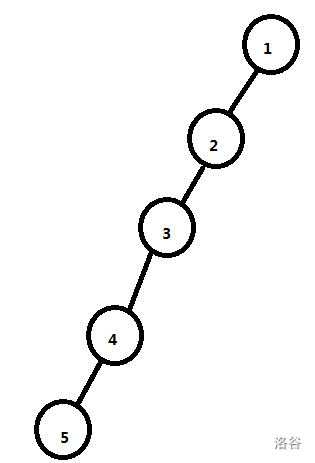
如果每次递归选择的根顺序是1 -> 2 -> 3 -> 4 -> 5,那么它将会递归五层,时间复杂度为 \(O(n^2)\)。所以我们每次要选择最合适的节点作为当前树的根。
那么什么样的根最合适呢?感性理解一下,要让它的子树大小尽量平均。这样可以减小树的规模,从而减少递归层数。所以最合适的根就是树的重心。
可以参考百科词条:
找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心,删去重心后,生成的多棵树尽可能平衡。
同时,重心有以下良好的性质:
- 删去该点后,最大子树的大小最小。
- 以树的重心为根的每棵子树大小不超过 \(\frac {n}{2}。\)
我们每次选取当前树的重心作为根节点,对于上面的链,它选择根的顺序为 3 -> 4,2 -> 5,1 ,只递归了三层。
对于它的时间复杂度可以从重心的第二条性质分析,每棵子树大小不超过 \(\frac {n}{2}\) ,每层递归,树的规模至少减半,所以递归层数是 \(log\ n\),寻找重心每层递归也会遍历所有节点,所以时间复杂度为 \(O(n\ log\ n)\)。
实现:
为了方便看懂后面代码,先看我的存图方式:
struct edge{
int v,w,next;
}e[2*maxn];
int en,head[maxn];//en为边数
inline void insert(int u,int v,int w){
e[++en].v=v;
e[en].w=w;
e[en].next=head[u];
head[u]=en;
}
对于点分治一般会有这样几个函数:
void getroot(int u,int fa,int sum)//查询子树重心
void getdis(int u,int fa,int dis)//遍历子树得到各种数据
void calc(int u)//计算当前子树的贡献
void solve(int u)//分治递归函数
先看solve函数:
void solve(int u){//分治递归函数
vis[u]=true;//当前节点打标记,防止在子树中搜索时搜到子树上面的节点
calc(u);//计算当前节点为根的贡献
for(int i=head[u];i;i=e[i].next){
int v=e[i].v;
if(vis[v])continue;
//递归分治
root=0;
getroot(v,0,siz[v]);
solve(root);
}
}
再看getroot函数:
void getroot(int u,int fa,int sum){//查询子树重心
//注意sum是当前这棵要找重心的树的大小
siz[u]=1,maxp[u]=0;
//siz为以u为根的子树大小,maxp为以u为根的最大子树的大小
for(int i=head[u];i;i=e[i].next){
int v=e[i].v;
if(v==fa||vis[v])continue;
getroot(v,u,sum);
siz[u]+=siz[v];
maxp[u]=max(maxp[u],siz[v]);//更新最大子树
}
maxp[u]=max(maxp[u],sum-siz[u]);//这是u节点上面的节点数,不在u的子树内,用容斥思想理解
if(!root||maxp[u]<maxp[root])root=u;//更新重心,参考重心定义:其所有的子树中最大的子树节点数最少
}
然后是getdis函数:
void getdis(int u,int fa,int dis){
//getdis就是遍历整棵树得到有用信息
a[++tot]=u;//一般会把所有节点存在一个数组中方便计算和统计
d[u]=dis;//到根节点的距离
dist[u]=dist[fa]+1;//到根节点的边数
//这里还可以有各种其他信息,比如u属于树的那棵子树
for(int i=head[u];i;i=e[i].next){
int v=e[i].v,w=e[i].w;
if(v==fa||vis[v])continue;
getdis(v,u,dis+w);
}
}
最后是calc函数:
void calc(int u){//计算当前子树的贡献
tot=0;//a数组的总节点数
a[++tot]=u;//有时会把根节点也放入a数组进行统计
//注意在统计 “u属于树的那棵子树” 时一般把根节点设为自己
d[u]=0;
dist[u]=0;
for(int i=head[u];i;i=e[i].next){
int v=e[i].v,w=e[i].w;
if(vis[v])continue;
getdis(v,u,w);
}
//下面的位置就是根据题目进行统计的地方了,一般技巧有:根据d[x]来sort a数组;单调队列;双指针;二分……也可以在上面的循环中对每棵子树分别处理。
dosomething;
}
在main函数中一般只有
//input
//建图
getroot(1,0,n);
solve(root);
//output
是不是非常的简单呢?
例题:
1.P3806 【模板】点分治1
这就是道点分治模板题。统计路径可以考虑把节点按照到根的距离排序,a[x]是按照到根的距离排序后的所有节点,d[x]是节点到根的距离。排序部分就是:
bool cmp(int x,int y){return d[x]<d[y];}
sort(a+1,a+tot+1,cmp);
用l,r表示两个节点在排序后数组中的位置,发现随着l变大,r是单调减的,所以可以双指针维护。
如果d[a[l]]+d[a[r]]>k,那么r--;如果d[a[l]]+d[a[r]]<k,那么l++。
但是需要注意可能会有a[l]和a[r]在同一棵子树的情况,此时不能被统计,因为有被多计算的路径,所以我们再维护一个b[x]存储x所属的子树根,特别的,令b[root]=root。
当d[a[l]]+d[a[r]]==k时,如果b[a[l]]!=b[a[r]]那么直接统计,如果b[a[l]]==b[a[r]],那么移动指针,考虑移l还是移r,如果d[a[r]]==d[a[r-1]]那么优先移r,否则,移动l,可以根据d[a[x]]的单调增来思考。
另外有多个询问,所以将询问储存下来,对每个询问跑双指针,如果满足条件记录一下即可。
代码:
#include<bits/stdc++.h>
using namespace std;
const int maxn=40005;
#define in read()
inline int read(){
int p=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){p=p*10+c-'0';c=getchar();}
return p*f;
}
int n,m,query[101];
int root,tot,d[maxn],b[maxn],a[maxn],siz[maxn],maxp[maxn];
bool vis[maxn],ok[maxn];
struct edge{
int v,w,next;
}e[2*maxn];
int en,head[maxn];
inline void insert(int u,int v,int w){
e[++en].v=v;
e[en].w=w;
e[en].next=head[u];
head[u]=en;
}
inline void getroot(int u,int fa,int sum){
siz[u]=1,maxp[u]=0;
for(int i=head[u];i;i=e[i].next){
int v=e[i].v;
if(v==fa||vis[v])continue;
getroot(v,u,sum);
siz[u]+=siz[v];
maxp[u]=max(maxp[u],siz[v]);
}
maxp[u]=max(maxp[u],sum-siz[u]);
if(!root||maxp[u]<maxp[root])root=u;
}
inline bool cmp(int x,int y){
return d[x]<d[y];
}
inline void getdis(int u,int fa,int dis,int from){
a[++tot]=u;
d[u]=dis;
b[u]=from;
for(int i=head[u];i;i=e[i].next){
int v=e[i].v,w=e[i].w;
if(v==fa||vis[v])continue;
getdis(v,u,dis+w,from);
}
}
inline void calc(int u){
tot=0;
a[++tot]=u;
d[u]=0;
b[u]=u;
for(int i=head[u];i;i=e[i].next){
int v=e[i].v,w=e[i].w;
if(vis[v])continue;
getdis(v,u,w,v);
}
sort(a+1,a+tot+1,cmp);
for(int i=1;i<=m;i++){
int l=1,r=tot;
while(l<r){
if(d[a[l]]+d[a[r]]>query[i])r--;
else if(d[a[l]]+d[a[r]]<query[i])l++;
else if(b[a[l]]==b[a[r]])
d[a[r]]==d[a[r-1]]?r--:l++;
else{ok[i]=true;break;}
}
}
}
inline void solve(int u){
vis[u]=true;
calc(u);
for(int i=head[u];i;i=e[i].next){
int v=e[i].v;
if(vis[v])continue;
root=0;
getroot(v,0,siz[v]);
solve(root);
}
}
signed main(){
n=in,m=in;
for(int i=1;i<n;i++){
int u=in,v=in,w=in;
insert(u,v,w);
insert(v,u,w);
}
for(int i=1;i<=m;i++){
query[i]=in;
if(!query[i])ok[i]=true;//注意特判,这种情况单调队列无法处理
}
getroot(1,0,n);
solve(root);
for(int i=1;i<=m;i++)
if(ok[i])printf("AYE\n");
else printf("NAY\n");
return 0;
}
2.P4178 Tree
和上题比区别不大,一样排序,需要再维护一个f[x]表示在l和r之间x子树的节点数,可以在l和r移动时动态维护。这样当d[a[l]]+d[a[r]]<=m时,对于l到r中的所有不属于b[a[l]]子树的节点都能与a[l]被统计,即ans+=r-l+1-f[b[a[l]]];,另外单独放出这段代码,注意思考为什么这样统计,为什么不重不漏。
int l=1,r=tot;
while(l<r){
while(l<r&&d[a[l]]+d[a[r]]<=m){
ans+=r-l+1-f[b[a[l]]];
--f[b[a[l]]];
l++;
}
--f[b[a[r]]];
r--;
}
代码:
#include<bits/stdc++.h>
using namespace std;
const int maxn=40005;
#define in read()
inline int read(){
int p=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){p=p*10+c-'0';c=getchar();}
return p*f;
}
int n,m,ans;
int root,tot,d[maxn],b[maxn],a[maxn],siz[maxn],maxp[maxn];
bool vis[maxn];
int f[maxn];
struct edge{
int v,w,next;
}e[2*maxn];
int en,head[maxn];
inline void insert(int u,int v,int w){
e[++en].v=v;
e[en].w=w;
e[en].next=head[u];
head[u]=en;
}
inline void getroot(int u,int fa,int sum){
siz[u]=1,maxp[u]=0;
for(int i=head[u];i;i=e[i].next){
int v=e[i].v;
if(v==fa||vis[v])continue;
getroot(v,u,sum);
siz[u]+=siz[v];
maxp[u]=max(maxp[u],siz[v]);
}
maxp[u]=max(maxp[u],sum-siz[u]);
if(!root||maxp[u]<maxp[root])root=u;
}
inline bool cmp(int x,int y){
return d[x]<d[y];
}
inline void getdis(int u,int fa,int dis,int from){
a[++tot]=u;
d[u]=dis;
b[u]=from;
f[from]++;
for(int i=head[u];i;i=e[i].next){
int v=e[i].v,w=e[i].w;
if(v==fa||vis[v])continue;
getdis(v,u,dis+w,from);
}
}
inline void calc(int u){
memset(f,0,sizeof(f));
tot=0;
a[++tot]=u;
d[u]=0;
b[u]=u;
f[u]++;
for(int i=head[u];i;i=e[i].next){
int v=e[i].v,w=e[i].w;
if(vis[v])continue;
f[v]=0;
getdis(v,u,w,v);
}
sort(a+1,a+tot+1,cmp);
int l=1,r=tot;
while(l<r){
while(l<r&&d[a[l]]+d[a[r]]<=m){
ans+=r-l+1-f[b[a[l]]];
--f[b[a[l]]];
l++;
}
--f[b[a[r]]];
r--;
}
}
inline void solve(int u){
vis[u]=true;
calc(u);
for(int i=head[u];i;i=e[i].next){
int v=e[i].v;
if(vis[v])continue;
root=0;
getroot(v,0,siz[v]);
solve(root);
}
}
signed main(){
n=in;
for(int i=1;i<n;i++){
int u=in,v=in,w=in;
insert(u,v,w);
insert(v,u,w);
}
m=in;
getroot(1,0,n);
solve(root);
printf("%d",ans);
return 0;
}
3.例题推荐:
P2634 [国家集训队]聪聪可可.
P4149 [IOI2011]Race.
小结:
其实点分治理解之后并不难,需要思考的只是如何利用各种信息和技巧快速地统计。
题外话:
因为我太菜了,所以可能还有其他点分治的技巧和操作我还不知道


