浅谈KMP算法

一、介绍

烤馍片KMP算法是用来处理字符串匹配问题的。比如说给你两个字符串A,B，问B是不是A的子串？

比如，eg就是aeggx的子串

一般讲字符串A称为主串，用来匹配的B串称为模式串

定义n为字符串A的长度，m为字符串B的长度（m≤n）

如果用暴力枚举法，时间复杂度为O(NM)

而KMP算法的时间复杂度在最坏的情况下为O(N)，十分搞笑高效

↑如果看到这张图饿了，去吃饭，吃完饭再来学KMP

二、烤馍片的流程

step1：把馍片做出来（要想烤馍片，首先得有馍片可以烤）

假设A=“xzxzxqxzxzq”，B=“xzxqxz”，一起来看看这两个馍片字符串如何匹配

step2：烤箱预热，馍片上撒调料

这两个馍片字符串都有各自的调料。A的调料指针是i，B的调料指针是j。

step3：扔到烤箱里，烤！

在高温的作用下，烤箱里发生了微妙的反应，两块馍片也慢慢烤熟，香气充盈……

现在开始烤馍片匹配字符串

假设现在A[i-j+1…i]和B[1…j]两个馍片已经烤熟了两个长度均为j的字符串完全匹配了

很容易想到，下面一步要继续匹配A[i+1]和B[j+1]

当A[i+1]=B[j+1](相同)时，i和j均加一并继续烤重复以上步骤

当A[i+1]≠B[j+1]（不相同）时

KMP算法的策略是减小j的值使得A[i-j+1…i]和B[1…j]依然匹配并继续尝试A[i+1]和B[j+1]的值

以样例为例：

i = 1 2 3 4 5 6 7 8 9 10 11

A= x z x z x q x z x z q

B= x z x q x z

j= 1 2 3 4 5 6

从头烤匹配，i=j=2时都没问题

当i=j=3时，A[i+1]='z'，B[j+1]='q'，A[i+1]≠B[j+1]

那么我们就要减小j值不然就烤糊了

设j减小后变为k

那么k应该是多少呢

由于当前的字符串是已经烤好了的已匹配的，所以k值要尽可能的大，这样馍片就会更好吃匹配的就会尽可能长。

此外，新的k值还要保证B[1…j]中的头k个字符和后k个字符相同

个人认为这里比较难理解，结合图像来看：

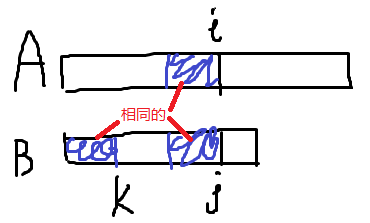
如图，A和B分别以i，j结尾的一段是匹配的，为了可以继续烤匹配，B[1…k]和A[i-k+1…i]也要是匹配的（这样才可以继续匹配A[i+1]和B[k+1]），因此，B[1…j]的开头k个字符和末尾k个字符必须要匹配。

于是图就变成了这样：

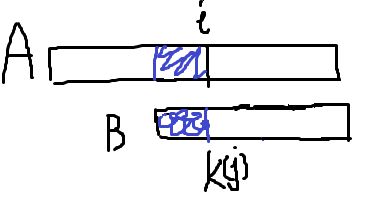
以样例为例，B[1…3]=xzx，开头一个和最后一个字符都是x，恰巧A[4]=B[2]，所以j的值变为1，然后就可以继续烤匹配了

i = 1 2 3 4 5 6 7 8 9 10 11

A= x z x z x q x z x z q

B= x z x q x z

j= 1 2 3 4 5

注意：有的时候直到j=0都无法匹配，这时需要增加i并忽略j，直到A[i]=B[1]为止。

从样例可以看出，k的值与i无关，只与j有关，且每个j值仅对应一个k值。因此，我们可以开一个数组提前将每个j对应的k值存起来，这就是KMP算法中的nxt数组（由于C++中变量名叫next有一些问题。所以通常叫nxt）。nxt[j]表示当匹配到B数组第j个字母而第j+1个字母不能匹配时，k值最大是多少。记住，k值应满足B[1…k]=B[j-k+1…j]且尽可能大（k<j）。

然后，就可以继续烤匹配了。

step4：出炉

当馍片烤好了，就可以出炉了

当j=m时，就匹配完成了

此时依题目要求而定

若题目只要回答B是不是A的子串，输出，结束

若题目要寻找B作为子串出现的次数，则继续寻找

↑香香的烤面筋馍片

下面是代码实现

匹配，输出位置：

//这里数组从1开始 
j=0;
for(i=0;i<n;i++)
{
    while(j>0 && a[i+1]!=b[j+1]) j=nxt[j];//j未减小到0且不能继续匹配，减小j的值
    if(a[i+1]==b[j+1]) j++;//能继续匹配，j的值增加
    //若j==0仍不能匹配，由于循环i的值会自动增加
    if(j==m)//找到一处匹配
    {
        printf("%d\n",i+1-m+1);//输出子串在主串中的位置
        j=nxt[j];//继续匹配 
    }
}

这是代码1

如果若干子串在主串中的位置不能重复，只需将j=nxt[j]改成j=0即可：

//这里数组从1开始 
j=0;
for(i=0;i<n;i++)
{
    while(j>0 && a[i+1]!=b[j+1]) j=nxt[j];//j未减小到0且不能继续匹配，减小j的值
    if(a[i+1]==b[j+1]) j++;//能继续匹配，j的值增加
    //若j==0仍不能匹配，由于循环i的值会自动增加
    if(j==m)//找到一处匹配
    { 
        printf("%d\n",i+1-m+1);//输出子串在主串中的位置
        j=0;//从头开始匹配，保证不重复 
    } 
}

这是代码2

预处理nxt数组：

//这里数组从1开始 
p[1]=j=0;
for(i=1;i<m;i++)
{
    while(j>0 && b[i+1]!=b[j+1]) j=nxt[j];//j未减小到0且不能继续匹配，退一步 
    if(b[i+1]==b[j+1]) j++;//能继续匹配，j的值增加
    //若j==0仍不能匹配，由于循环i的值会自动增加
    nxt[i+1]=j;//nxt数组赋值 
}