周任务——矩阵和行列式

话说我一个初二的小蒟篛，给我布置线性代数（汗）。。。。。。

硬着头皮写博客

 

矩阵

• 第一部分 矩阵的定义

由 m × n 个数a_ij排成的m行n列的数表称为m行n列的矩阵，简称m × n矩阵。记作：

这m×n 个数称为矩阵A的元素，简称为元，数a_ij位于矩阵A的第i行第j列，称为矩阵A的(i,j)元，以数 a_ij为(i,j)元的矩阵可记为(a_ij)或(a_ij)_{m × n}，m×n矩阵A也记作A_mn。

元素是实数的矩阵称为实矩阵，元素是复数（实数和虚数）的矩阵称为复矩阵。而行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵

在计算机里，不就是我们常用的二维数组吗？

int a[1001][1001];

 

• 第二部分 矩阵的基本运算

矩阵的基本运算包括矩阵的加法，减法，数乘，转置，共轭和共轭转置

同型矩阵：行数和列数都相等的矩阵

一、加法

简单来说，就是把相同位置上的数加起来

矩阵的加法满足下列运算律(A，B，C都是同型矩阵)：

交换律：

 

 

 

结合律：

 

 

 

应该注意的是只有同型矩阵之间才可以进行加法

 

二、减法

和加法类似，把同型矩阵相同位置上的数相减

减法同样有交换律和结合律

 

三、数乘

一个数乘以矩阵，把矩阵中的每一个元素都与该数相乘，如：

矩阵的加减法和矩阵的数乘合称矩阵的线性运算

 

四、矩阵×矩阵

重点来了！！！

定义矩阵A_mp，B_pn，即A的列数等于B的行数，这时才能进行乘法，否则乘法就没有意义了

乘出来的矩阵C_mn，矩阵C的行数是A的行数，列数是B的列数（那个不相等的数）

那里面的元素呢？

C_ij=A的第i行（p个数）和B的第j列（同样是p个数，这就是为什么要求A的列数等于B的行数）对应位置上数的乘积的和

举个例子：

C₁₁=A11×B11+A12×B21+A13×B31=1×1+2×2+3×3=14

即A的第一行和B的第一列

矩阵的乘法也满足结合律，但不满足交换律

 

五、矩阵乘法的应用

看了这么多，你可能觉得矩阵并没有什么用。的确没有用。

 

斐波那契数列（洛谷1962）

题目背景

大家都知道，斐波那契数列是满足如下性质的一个数列：

• f(1) = 1

• f(2) = 1

• f(n) = f(n-1) + f(n-2) (n ≥ 2 且 n 为整数)

题目描述

请你求出 f(n) mod 1000000007 的值。

输入输出格式

输入格式：

·第 1 行：一个整数 n

输出格式：

第 1 行： f(n) mod 1000000007 的值

输入输出样例

输入样例#1： 

5

输出样例#1： 

5

输入样例#2： 

10

输出样例#2： 

55

说明

对于 60% 的数据： n ≤ 92

对于 100% 的数据： n在long long(INT64)范围内。

 

解析：

n那么大，不能用普通的递推，那怎么办呢？

观察这个矩阵：

1 1

1 0

把这个矩阵平方一下：

1×1+1×1 1×1+1×0        ==》 2 1

1×1+1×0 1×1+1×0        ==》 1 1

立方：

3 2

2 1

多试几次，可以发现矩阵1110的n次方得到的数是斐波那契数列中的第n+1，n，n，n-1项。

得到了这条结论，下面就很简单了，可以用快速幂运算，得出答案

快速幂运算：

M偶数：N^M=N^{2^(M/2)}

M奇数：N^M=N*N^{2^(M/2)}

附上代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<cstdlib>
#define mod 1000000007
using namespace std;

long long n;

struct node
{
    long long a[5][5];
}x,ans;

node mi(node w,node y)
{
    node tmp;
    int i,j,k;
    memset(tmp.a,0,sizeof(tmp.a));
    for(i=0;i<2;i++)
        for(j=0;j<2;j++)
            for(k=0;k<2;k++)
                tmp.a[i][j]=(tmp.a[i][j]+w.a[i][k]*y.a[k][j])%mod;
    return tmp;
}

int main()
{
    scanf("%lld",&n);
    if(n==0)
    {
        cout<<0;
        return 0;
    }
    if(n==1 || n==2)
    {
        cout<<1;
        return 0;
    }
    x.a[0][0]=ans.a[0][0]=1; x.a[0][1]=ans.a[0][1]=1;
    x.a[1][0]=ans.a[1][0]=1; x.a[1][1]=ans.a[1][1]=0;
    while(n)
    {
        if(n%2==1) ans=mi(ans,x);
        n/=2;
        x=mi(x,x);
    }
    cout<<ans.a[1][1]%mod;
    return 0;
}

 

 六、矩阵的转置

就是把矩阵整个转一下，行变成列，列变成行，记符号为T。如下：

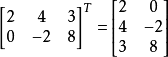
把一个矩阵转置两次，等同于不转置，即（A^T）^T=A