github:代码实现之神经网络
本文算法均使用python3实现
1. 什么是神经网络
人工神经网络(artificial neural network,缩写ANN),简称神经网络(neural network,缩写NN)或类神经网络,是一种模仿生物神经网络(动物的中枢神经系统,特别是大脑)的结构和功能的数学模型或计算模型,用于对函数进行估计或近似。
神经网络主要由:输入层,隐藏层,输出层构成。当隐藏层只有一层时,该网络为两层神经网络,由于输入层未做任何变换,可以不看做单独的一层。实际中,网络输入层的每个神经元代表了一个特征,输出层个数代表了分类标签的个数(在做二分类时,如果采用sigmoid分类器,输出层的神经元个数为1个;如果采用softmax分类器,输出层神经元个数为2个),而隐藏层层数以及隐藏层神经元是由人工设定。一个基本的三层神经网络可见下图:
1.1 从逻辑回归到神经元
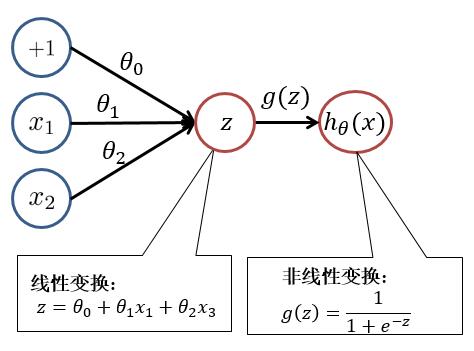
为了便于大家理解,我们先回顾一下逻辑回归。逻辑回归模型如下: $$ h_\theta(x) = \frac{1}{1+e{-\thetaT x}} $$
其中 $ z = \theta^T x = \theta_0 + \theta_1x_1 + \theta_2 x_2 $ , $ h_\theta(x) = g(z) = \frac{1}{1+e^{-z}} $
对此我们可以用以下结构进行理解:
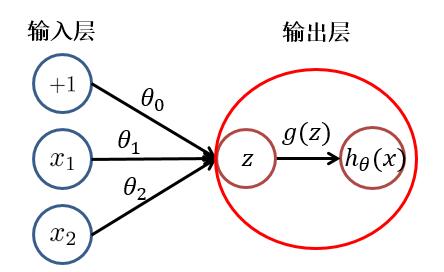
根据上图,我们可以看出,逻辑回归可以分为**线性变换**部分与**非线性变换**部分。而**只有输入层与输出层且输出层只有一个神经元**的神经网络的结构便于逻辑回归一致。只不过在神经网络中,**线性变换(求和)**与**非线性变换**被集成在一个神经元(隐藏层或输出层)中。如下图所示:
于是,对于具有多层或多个输出神经元的神经网络就不难理解了。其**每个**隐藏层**神经元**/输出层**神经元**的值(**激活值**),都是由上一层神经元,经过**加权求和**与**非线性变换**而得到的。其中**非线性变换函数(又被称为激活函数)**可以是: $ sigmoid、tanh、relu $ 等函数。
1.2 神经网络
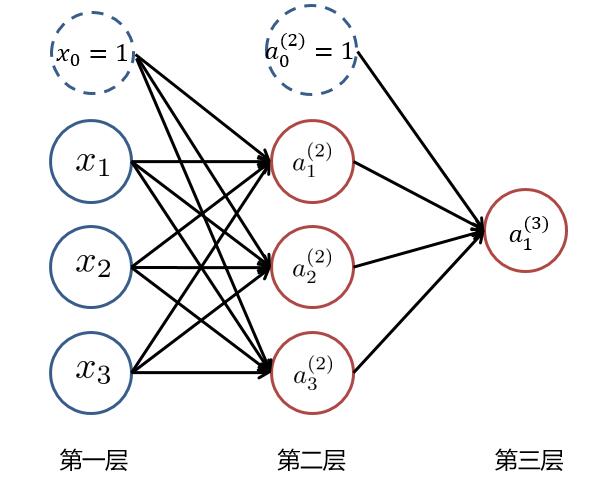
根据1.1中所讲述,我们可以得到以下这样一个基本的三层神经网络:
其中 $ x_i (i=1,2,3) $ 为输入层的值,$ a_i^{(k)} (k=1,2,3...,K;i=1,2,3...,N_k) $ ,表示第 $ k $ 层中,第 $ i $ 个神经元的激活值, $ N_k $ 表示第 $ k $ 层的神经元个数。当 $ k=1 $ 时即为输入层,即 $ a_i^{(1)} = x_i $ ,而 $ x_0 = 1 与 a_0^{(2)} =1 $ 为偏置项。
为了求最后的**输出值 $ h_\theta(x)=a_1^{(3)} $**,我们需要计算隐藏层中每个神经元的激活值 $ a_{ji}^{(k)} (k=2,3) $。而隐藏层/输出层的每一个神经元,都是由上一层神经元经过**类似逻辑回归**计算而来。我们可以使用下图进行理解:
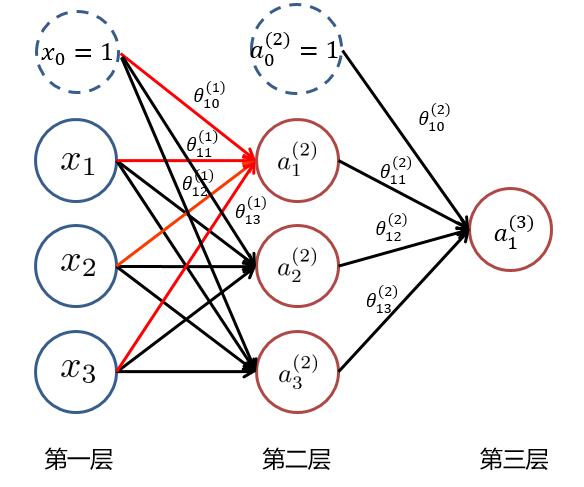
我们使用 $ \theta_{ji}^{(k)} $ 来表示第 $ k $ 层的参数(边权),其中下标 $ j $ 表示第 $ k+1 $ 层的第 $ j $ 个神经元,$ i $ 表示第 $ k $ 层的第 $ i $ 个神经元。于是我们可以计算出**隐藏层**的三个**激活值**:
$$ a_1^{(2)} = g(\theta_{10}^{(1)} x_0 + \theta_{11}^{(1)} x_1 + \theta_{12}^{(1)} x_2 +\theta_{13}^{(1)} x_3) $$
$$ a_2^{(2)} = g(\theta_{20}^{(1)} x_0 + \theta_{21}^{(1)} x_1 + \theta_{22}^{(1)} x_2 +\theta_{23}^{(1)} x_3) $$
$$ a_3^{(2)} = g(\theta_{30}^{(1)} x_0 + \theta_{31}^{(1)} x_1 + \theta_{32}^{(1)} x_2 +\theta_{33}^{(1)} x_3) $$
再将隐藏层的三个激活值以及偏置项( $ a_0^{(2)},a_1^{(2)},a_2^{(2)},a_3^{(2)} $ )用来计算出输出层神经元的**激活值**即为该神经网络的输出:
$$ a_1^{(3)} = g(\theta_{10}^{(2)} a_0^{(2)} + \theta_{11}^{(2)} a_1^{(2)} + \theta_{12}^{(2)} a_2^{(2)} +\theta_{13}^{(2)} a_3^{(2)}) $$
其中 $ g(z) $ 为**非线性变换函数(激活函数)**。
到此,我们就大致了解了什么是神经网络了。
1.3 为什么要使用神经网络
首先,神经网络应用在分类问题中效果很好。 工业界中分类问题居多。LR或者linear SVM更适用线性分类。如果数据非线性可分(现实生活中多是非线性的),LR通常需要靠特征工程做特征映射,增加高斯项或者组合项;SVM需要选择核。 而增加高斯项、组合项会产生很多没有用的维度,增加计算量。GBDT可以使用弱的线性分类器组合成强分类器,但维度很高时效果可能并不好。而神经网络在三层及以上时,能够很好地进行非线性可分。现在我们使用下面的例子进行一下解释。
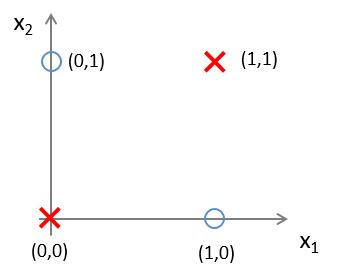
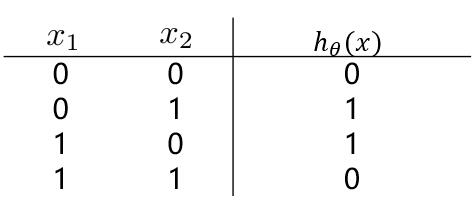
有这样一组样本,如下图:
若我们需要对上图中的样本进行分类,直观来看,**很难找到一条线性分类边界对其进行分类**,而观察上表中的输入输出值,我们可以看出分类结果与输入值是**异或**关系。**而逻辑回归可以通过改变参数,来实现“与”、“或”、“非”简单操作**。
(1)我们先来观察一下**逻辑回归**实现**逻辑“与”操作**,假设模型函数如下: $$ h_\theta^{(1)}(x) = g(-30 + 20x_1+20x_2) = \frac{1}{1+e^{-(-30 + 20x_1+20x_2)}} $$
对应结构与结果为:
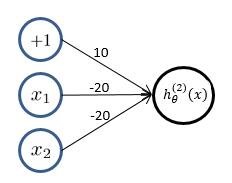
(2)**逻辑回归**实现**逻辑“或非”操作**,假设模型函数如下: $$ h_\theta^{(1)}(x) = g(-10 - 20x_1- 20x_2) = \frac{1}{1+e^{-(10 - 20x_1 - 20x_2)}} $$
对应结果为:
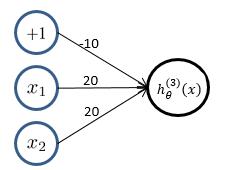
(3)**逻辑回归**实现**逻辑“或”操作**,假设模型函数如下: $$ h_\theta^{(1)}(x) = g(-10 + 20x_1 + 20x_2) = \frac{1}{1+e^{-(10 + 20x_1 + 20x_2)}} $$
对应结果为:
**观察(1)(2)中的 $ h_\theta^{(1)}(x) 与 h_\theta^{(2)}(x) $ 的值,通过“或”操作,便能够得到“异或”操作的结果。**
也就是说,若将三个**逻辑回归**操作进行**叠加**,便能够对上述例子进行**非线性分类**。大致结构图可理解为下:
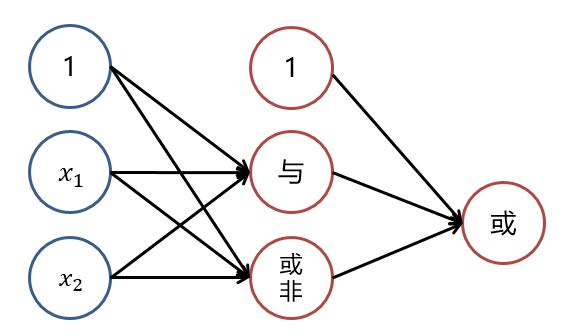
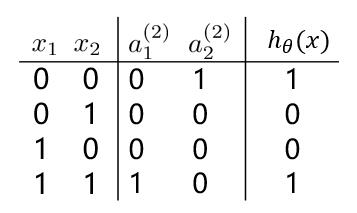
而对**线性分类器**的逻辑与和逻辑或的**组合**可以完美的对平面样本进行分类。
隐层决定了最终的分类效果 :
由上图可以看出,随着隐层层数的增多,凸域将可以形成任意的形状,因此可以解决任何复杂的分类问题。实际上,Kolmogorov理论指出:双隐层感知器就足以解决任何复杂的分类问题。
于是我们可以得出这样的结论:**神经网络**通过将线性分类器进行组合叠加,能够较好地进行**非线性分类**。
2.神经网络目标函数
同样的,对于神经网络我们也需要知道其目标函数,才能够对目标函数进行优化从而学习到参数。
假设神经网络的输出层只有一个神经元,该网络有 $ K $ 层,则其目标函数为(若不止一个神经元,每个输出神经元的目标函数类似,仅仅是参数矩阵的不同):
\[J(\theta) = - \frac{1}{m} [ \sum_{i=1}^m y^{(i)} \log(h_\theta(a^{(K-1)})) + (1-y^{(i)}) \log(1-h_\theta(a^{(K-1)}))] + \frac{\lambda}{2m} \sum_{k=1}^{K-1} \sum_{i=1}^{N_k} \sum_{j=1}^{N_{k+1}} (\theta_{ji}^{(k)})^2
\]
其中 $ a^{(i)} $ 倒数第2层的激活值,作为输出层的输入值。而其值为 $ a^{(k)} = g(a^{(k-1)}) $ , $ y^{(i)} $ 为实际分类结果 $ 0/1 $ , $ m $ 为样本数,$ N_k $ 为第 $ k $ 层的神经元个数。
3.神经网络优化算法
神经网络与普通的分类器不同,其是一个巨大的网络,最后一层的输出与每一层的神经元都有关系。而神经网络的每一层,与下一层之间,都存在一个参数矩阵。我们需要通过优化算法求出每一层的参数矩阵,对于一个有 $ K $ 层的神经网络,我们共需要求解出 $ K-1 $ 个参数矩阵。因此我们无法直接对目标函数进行梯度的计算来求解参数矩阵。
对于神经网络的优化算法,主要需要两步:前向传播(Forward Propagation)与反向传播(Back Propagation)
3.1 前向传播
前向传播就是从输入层到输出层,计算每一层每一个神经元的激活值。也就是先随机初始化每一层的参数矩阵,然后从输入层开始,依次计算下一层每个神经元的激活值,一直到最后计算输出层神经元的激活值。
以下面这个例子来看:
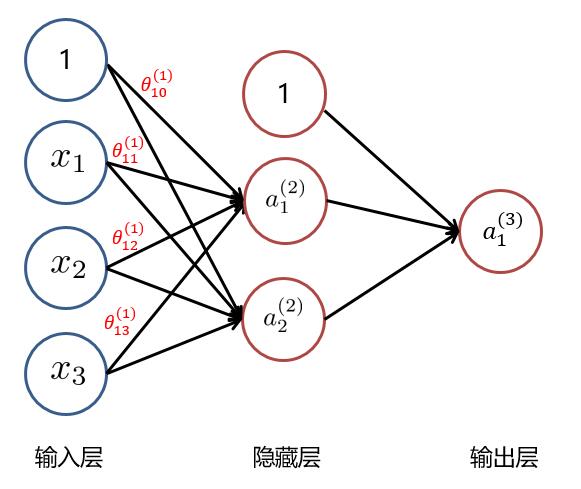
(1)随机初始化参数矩阵 $ \Theta^{(1)} 与 \Theta^{(2)} $ :
$$ \Theta^{(1)} = \begin{bmatrix} \theta_{10}^{(1)} & \theta_{11}^{(1)} & \theta_{12}^{(1)} & \theta_{13}^{(1)} \\ \theta_{20}^{(1)} & \theta_{21}^{(1)} & \theta_{22}^{(1)} & \theta_{23}^{(1)} \\ \end{bmatrix}
\Theta^{(2)} = \begin{bmatrix} \theta_{10}^{(2)} & \theta_{11}^{(2)} & \theta_{12}^{(2)} \\ \end{bmatrix} $$
(2)计算隐藏层的每个神经元激活值:
$$ a_1^{(2)} = g(\theta_{10}^{(1)} x_0 + \theta_{11}^{(1)} x_1 + \theta_{12}^{(1)} x_2 +\theta_{13}^{(1)} x_3) $$
$$ a_2^{(2)} = g(\theta_{20}^{(1)} x_0 + \theta_{21}^{(1)} x_1 + \theta_{22}^{(1)} x_2 +\theta_{23}^{(1)} x_3) $$
即:
$$ a^{(2)} = g(\Theta^{(1)} x) ,其中 a^{(2)} = \begin{bmatrix} a_1^{(2)} \\ a_2^{(2)} \\ \end{bmatrix} , x = \begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \\ \end{bmatrix} $$
(3)计算隐藏层的每个神经元激活值:
$$ a_1^{(3)} = g(\theta_{10}^{(2)} a_0^{(2)} + \theta_{11}^{(2)} a_1^{(2)} + \theta_{12}^{(2)} a_2^{(2)} ) $$
即:
$$ a^{(3)} = g(\Theta^{(2)} a^{(2)}) ,其中 a^{(2)} = \begin{bmatrix} a_0^{(2)} \\ a_1^{(2)} \\ a_2^{(2)} \\ \end{bmatrix} $$
以上便是**前向传播**计算**激活值**的过程。
3.2 反向传播
反向传播总的来说就是根据前向传播计算出来的激活值,来计算每一层参数的梯度,并从后往前进行参数的更新。
在介绍反向传播的计算步骤之前,我们先引入一个概念---除输入层外每个神经元节点的“损失” ,$ \delta_j^{k} $ 表示第 $ k $ 层第 $ j $ 个神经元的损失。
于是我们可以计算求得(除输入层)每一层神经元的损失(以上一个例子来解释):
\[\delta_1^{(3)} = a_1^{(3)} - y_1
\]
其中 $ y_1 $ 为实际值。向量化表示如下:
\[\delta^{(3)} = a^{(3)} - y
\]
\[\delta^{(2)} = ((\Theta^{(2)})^T) \delta^{(3)} \cdot \ast g'(z^{(2)})
\]
其中 $ \cdot \ast $ 表示两个矩阵对应位置上元素相乘, $ g'(z^{(2)}) $ 是对函数求导。而 $$ z^{(2)} = \begin{bmatrix} \theta_{10}^{(1)} x_0 + \theta_{11}^{(1)} x_1 + \theta_{12}^{(1)} x_2 +\theta_{13}^{(1)} x_3 \ \theta_{20}^{(1)} x_0 + \theta_{21}^{(1)} x_1 + \theta_{22}^{(1)} x_2 +\theta_{23}^{(1)} x_3 \ \end{bmatrix}$$
由上可看出,第二层的损失 $ \delta^{(2)} $ 是基于第三层的损失 $ \delta^{(3)} $ 计算而来。也就是说,我们可以先计算第三层的损失并对第二层的参数矩阵进行更新,再利用第三层的损失计算第二层的损失以及更新第一层的参数矩阵(至于为何可以这样进行,将在后面进行证明)。
于是,基于反向传播算法的梯度更新步骤如下:
(1)计算每一层的损失:$ \delta^{k} $(见上面所示)。
(2)计算每一层的 $ \Delta $ (初始化为0):$ \Delta^{(k)} = \Delta^{(k)} + \delta^{(k+1)} (a{(k)})T $
(3)计算每一个参数的梯度: $$ D_{ji}^{(k)} = \frac{1}{m} \Delta_{ji}^{(k)} + \lambda \Theta_{(ji)}^{(k)} , 如果 i \neq 0 $$ $$ D_{ji}^{(k)} = \frac{1}{m} \Delta_{ji}^{(k)} , 如果 i = 0 $$
也就是说 $ \frac{\delta J(\Theta)}{\delta \Theta_{ji}^{k}} = D_{ji}^{(k)} $。于是就可以使用梯度下降来进行参数的求解了。
3.3 反向传播的推导
大家可能都会有疑问,为什么求梯度时,要先对后一层进行计算,并利用其结果来求前一层的梯度?我们将针对如下例子进行推导证明:
第一层的参数为:
$$ \Theta^{(1)} = \begin{bmatrix} \theta_{10}^{(1)} & \theta_{11}^{(1)} & \theta_{12}^{(1)} & \theta_{13}^{(1)} \\ \theta_{20}^{(1)} & \theta_{21}^{(1)} & \theta_{22}^{(1)} & \theta_{23}^{(1)} \\ \end{bmatrix} $$
第二层的参数为:
$$ \Theta^{(2)} = \begin{bmatrix} \theta_{10}^{(2)} & \theta_{11}^{(2)} & \theta_{12}^{(2)} \\ \end{bmatrix} $$
我们先来对第二层的参数求梯度 $ \frac{\delta J(\Theta)}{\delta \theta^{(2)}} $ :
其中 $ y^i $ 为实际值, $ g(\theta^{(2)} a^{(2)}) = a^{(3)} $ 。
这一步的推导过程与逻辑回归一样,详细可参考[逻辑回归梯度求导过程](http://www.cnblogs.com/lliuye/p/9129493.html)。
现在我们来对第一层的参数求梯度 $ \frac{\delta J(\Theta)}{\delta \theta^{(1)}} $ :
先对中括号内的求导:
故:
对比着3.2中的公式,我们可以看出,第 $ k $ 层的梯度可以根据第 $ k+1 $ 层的**损失**来计算(上式是用第 $ 2 $ 的损失来推导第 $ 1 $ 层的梯度)。
到此,反向传播的推导过程就完成了。如果对式子还有不理解的,可以自己动手多试试。
4.神经网络算法分析
该部分参考博文[3]
(1)理论上,单隐层神经网络可以逼近任何连续函数(只要隐层的神经元个数足够)
(2)对于一些分类数据(比如CTR预估),3层神经网络效果优于2层神经网络,但如果把层数不断增加(4,5,6层),对最后的结果的帮助没有那么大的跳变。
(3)提升隐层数量或者隐层神经元个数,神经网络的“容量”会变大,空间表达能力会变强。
(4)过多的隐层和神经元结点会带来过拟合问题。
(5)不要试图降低神经网络参数量来减缓过拟合,用正则化或者dropout层。
注意:在代码中对参数的初始化并不是使用0来初始化,还是在范围 $ [-\epsilon,\epsilon] $ 间随机初始化。对应代码为:
Theta = np.random.rand(nextUnit, Unit+1) * 2 * epsilon - epsilon
引用及参考:
[1] 《Machine Learning》Andrew Ng
[2] https://www.jianshu.com/p/a3b89d79f325
[3] https://blog.csdn.net/leiting_imecas/article/details/60463897
[4] https://blog.csdn.net/a819825294/article/details/53393837
写在最后:本文参考以上资料进行整合与总结,属于原创,文章中可能出现理解不当的地方,若有所见解或异议可在下方评论,谢谢!
若需转载请注明:https://www.cnblogs.com/lliuye/p/9183914.html




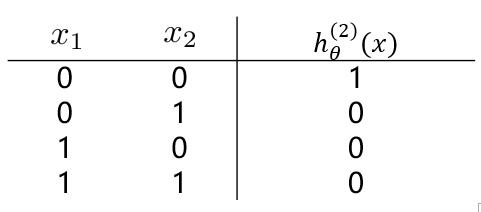
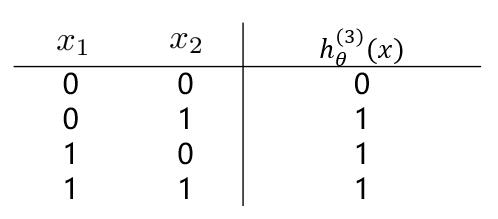
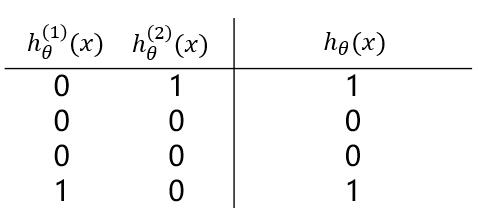
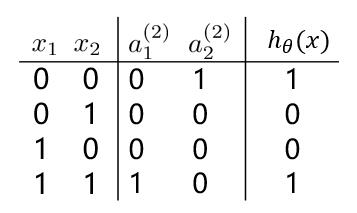







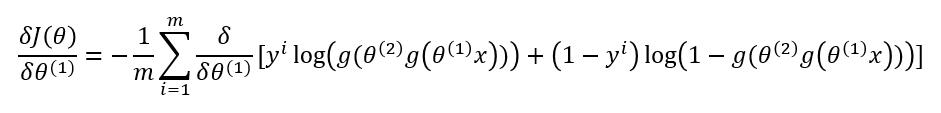
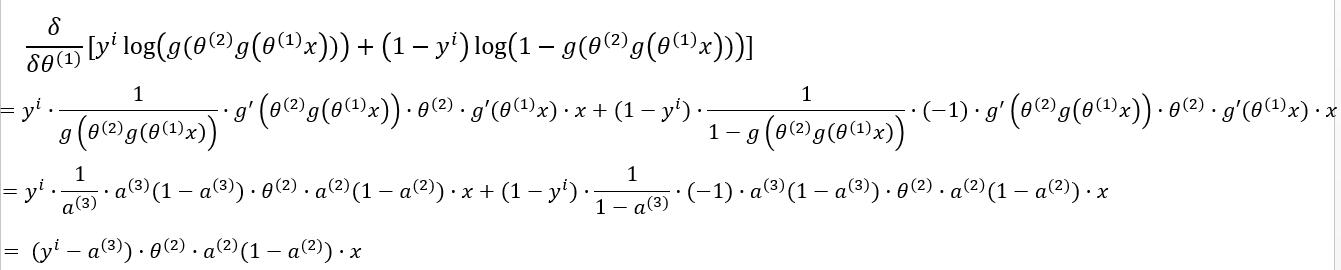



 浙公网安备 33010602011771号
浙公网安备 33010602011771号