异常检测(Anomaly Detection)

github：代码实现
本文算法均使用python3实现

---

1. 异常检测

1.1 异常检测是什么？

  异常检测即为发现与大部分样本点不同的样本点，也就是离群点。
  我们可通过下面这个例子进行理解，在飞机引擎制造商对制造好的飞机引擎进行测试时，选择了对飞机引擎运转时产生的热量以及震动强度进行测试，测试后的结果如下：

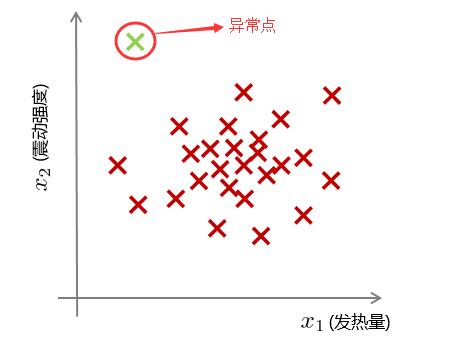
  很明显我们能够看出，存在一个点（绿色），其热量较低时震动强度却很高，它在坐标轴中的分布明显偏离了其它的样本点。因此我们可以认为这个样本点就是异常点即离群点。

1.2 异常检测的方法

  异常检测不同于监督学习，其正样本（异常点）容量明显远小于负样本（正常点）的容量，因此我们并不能使用监督学习的方法来进行异常检测的判断。对于异常检测主要有以下几种方法：
  （1）基于模型的技术：许多异常检测技术首先建立一个数据模型，异常是那些同模型不能完美拟合的对象。例如，数据分布的模型可以通过估计概率分布的参数来创建。在假设一个对象服从该分布的情况下所计算的值小于某个阈值，那么可以认为他是一个异常对象。
  （2）基于邻近度的技术：通常可以在对象之间定义邻近性度量，异常对象是那些远离大部分其他对象的对象。当数据能够以二维或者三维散布图呈现时，可以从视觉上检测出基于距离的离群点。
  （3）基于密度的技术：对象的密度估计可以相对直接计算，特别是当对象之间存在邻近性度量。低密度区域中的对象相对远离近邻，可能被看做为异常。
  本文主要讨论基于模型的异常检测方法

1.3 基于模型的异常检测基本步骤

  （1）对样本集进行建模： $ P(x) $ ，即对 $ x $ 的分布概率进行建模
  （2）对于待检测样本 $ x_{test} $ ，若 $ P(x_{test}) < \epsilon $ 则样本为异常，若 $ P(x_{test}) > \epsilon $ 则样本为正常。

---

2. 高斯分布

2.1 什么是高斯分布？

  高斯分布即为正态分布。是指对于样本 $ x \in R $ ，假设其服从均值 $ \mu $ ,方差 $ \sigma^2 $ 的高斯分布，可记为 $ x \sim N(\mu, \sigma^2) $ 。其概率密度函数可记为： $$ P(x;\mu, \sigma^2) = \frac{1}{\sqrt{2 \pi} \sigma} exp(- \frac{(x-\mu)^2}{2 \sigma^2}) $$
  概率密度函数图像如下：

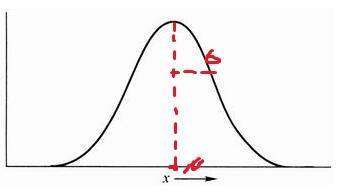
  其中均值 $ \mu $ 决定了曲线的中心位置，而 $ \sigma $ 决定了曲线的宽度。
  差别可见下图：

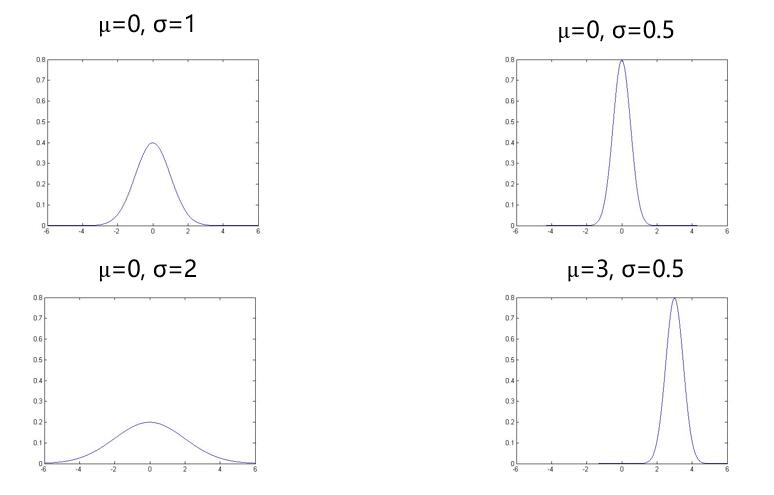
2.2 高斯分布的参数估计

  对于数据集 $ D=\lbrace x^{(1)}, x^{(2)},...,x \rbrace $ ，其中 $ x^{(i)} $ 为一维的，即只有一个特征，共有 $ m $ 个样本。我们对高斯分布的参数 $ \mu , \sigma^2 $ 进行参数估计：

\[\mu = \frac{1}{m} \sum_{i=1}^m x^{(i)} \]

\[\sigma^2 = \frac{1}{m} \sum_{i=1}^m (x^{(i)}-\mu)^2 \]

  该参数估计使用极大似然估计法，详细可参考极大似然估计法相关博文

2.3 基于高斯分布的异常检测

  我们是如何利用高斯分布进行异常检测的呢？
  假设对于样本集中的每个特征都相互独立且都服从高斯分布（当不服从高斯分布时，使用 $ \log(x) $ 来转换），因此我们需要计算出所有特征对应的高斯分布的参数，再通过计算 $ P(x) = P(x_1;\mu_1,\sigma_1^{2)P(x_2;\mu_2,\sigma_2}2) \cdots P(x_n;\mu_n,\sigma_n^2) $ ，比较 $ P(x) $ 与阈值 $ \epsilon $ 即可。
  具体步骤如下：
  （1）使用训练集拟合参数： $ \mu_1,\mu_2,...,\mu_n；\sigma_1^2, \sigma_2^{2,...,\sigma_n}2 $

\[\mu_j = \frac{1}{m} \sum_{i=1}^m x_j^{(i)} \]

\[\sigma_j^2 = \frac{1}{m} \sum_{i=1}^m (x_j^{(i)}-\mu_j)^2 \]

    其中 $ j=1,2...,n $ 表示特征数， $ i=1,2,...,m $ 为样本数。
  （2）给定新样本 $ x $ ,计算 $ P(x) $

\[P(x) = \prod_{j=1}^n P(x_j;\mu_j,\sigma_j^2) = \prod_{j=1}^n \frac{1}{\sqrt{2 \pi} \sigma_j} exp(- \frac{(x_j-\mu_j)^2}{2 \sigma_j^2}) \]

  （3）若 $ P(x) < \epsilon $ 则判断为异常点。

2.4 异常检测算法的评估指标

  如何评价一个异常检测算法呢？
  和监督学习算法一样，我们可以对样本集进行划分，划分成训练集，交叉验证集，测试集。对于训练集，均是正常样本；而交叉验证集与测试集存在大量正常样本与少数异常样本。我们通过训练集来建立概率模型，使用交叉验证集进行参数的调整（比如 $ \epsilon $ 的选择），使用测试集进行模型的测试与模型的评估。
  由于异常检测是有偏数据，因此不可以使用分类准确率。而其可以使用的评估指标有：
  （1）True Positive,False Positive,False Negative, True Negative
  （2）Precision.Recall
  （3）F1-score

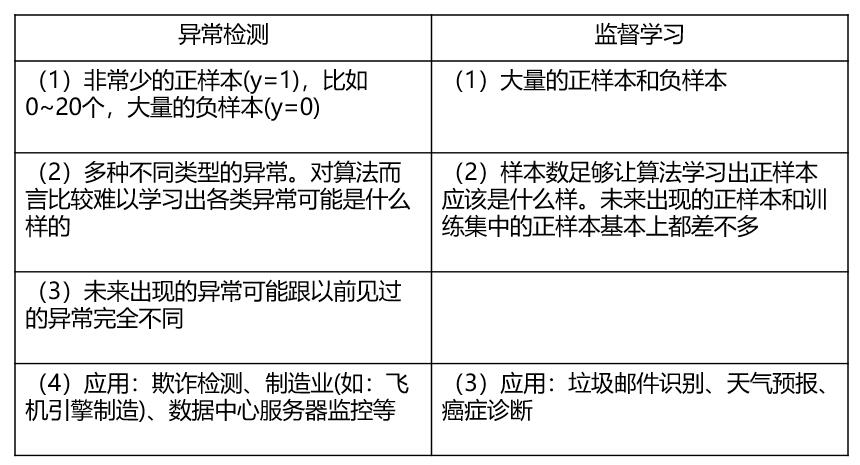
2.5 异常检测 v.s. 监督学习

---

3. 多元高斯分布

  利用高斯分布进行异常检测存在一个巨大的前提：各个特征之间独立同分布。往往在现实生活中并不能保证各特征之间是独立同分布的，而是或多或少有一些相关性。我们使用下面的例子进行理解：

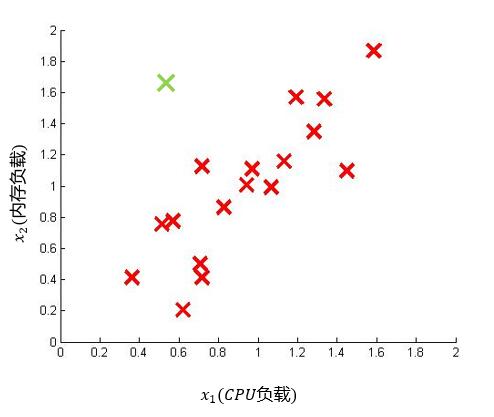
  对于上图我们可以看出，存在一个异常点（绿色）。假如我们按照基于独立同分布的高斯分布进行分析，将样本点分别投影在两个坐标轴中，见下图：

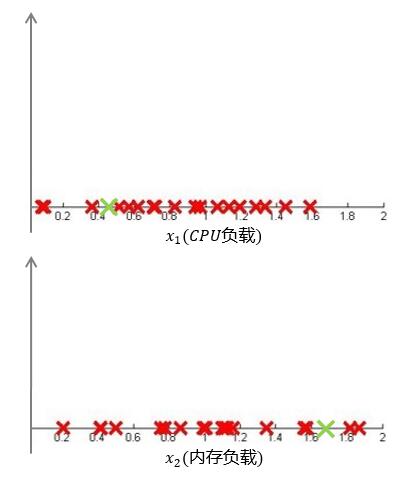
  由于异常点存在于正常点之间，根据计算并不满足 $ P(x) < \epsilon $ ，因此我们很容易将该点划分为正常样本。那么对于这样的数据集，我们该如何进行异常检测呢？答案是多元高斯分布

3.1 什么是多元高斯分布？

  多元高斯分布不再是对特征单独建模，而是对所有特征进行统一建模。其模型参数为 $ \mu \in R^n , \Sigma \in R^{n \times n} $ 。其概率密度函数可记为：

\[P(x;\mu, \Sigma) = \frac{1}{(2 \pi)^{\frac{n}{2}} |\Sigma|^{\frac{1}{2}}} exp(-\frac{1}{2} (x- \mu)^T \Sigma^{-1} (x- \mu)) \]

  其中 $ \mu = [\mu_1,\mu_2,...,\mu_n]^T $ 是特征均值向量，$ \Sigma $ 为协方差矩阵。
  以下是参数 $ \mu , \Sigma $ 对于概率分布函数的图像影响：

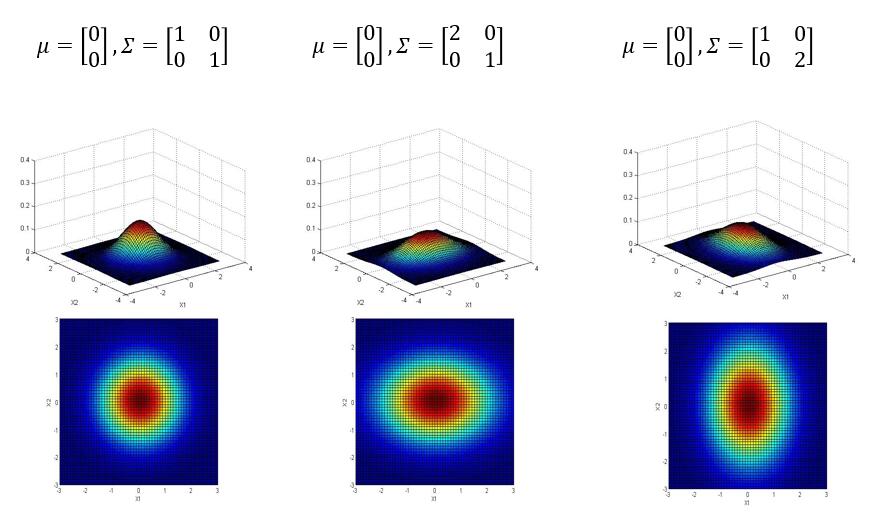
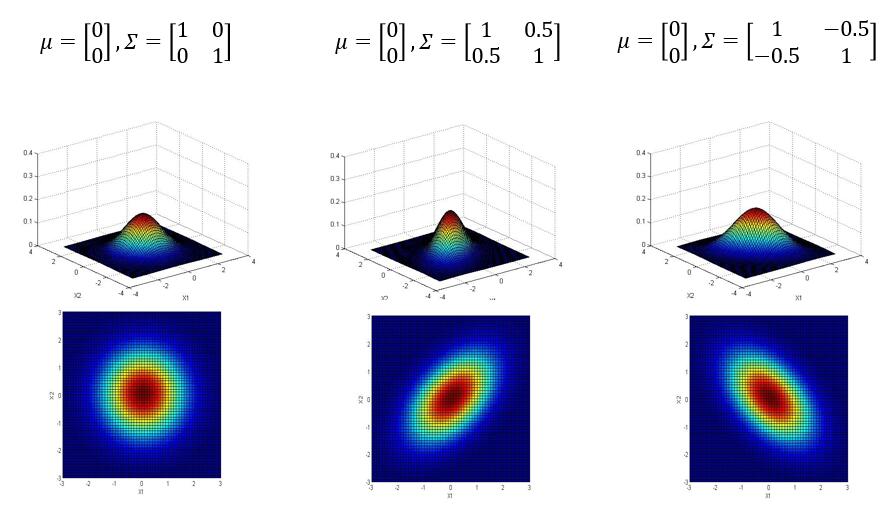
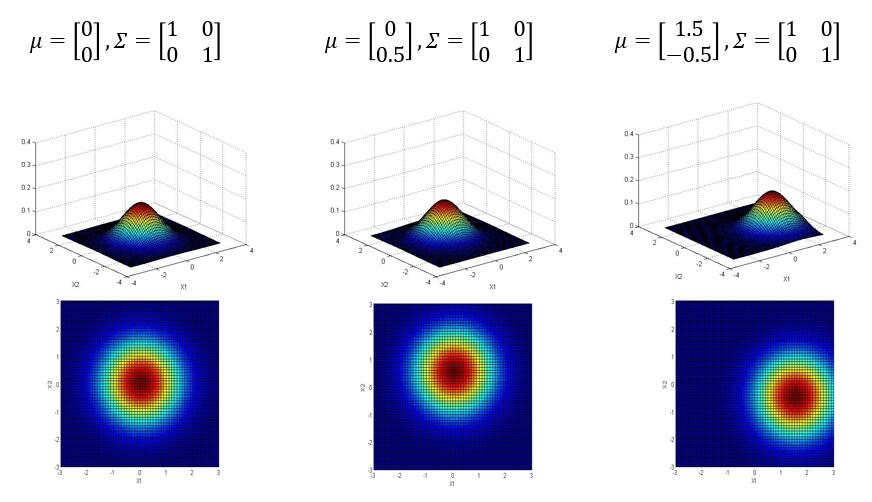
3.2 多元高斯分布的参数估计

对于数据集 $ D=\lbrace x^{(1)}, x^{(2)},...,x \rbrace $ ，其中 $ x^{(i)} $ 为 $ n $ 维的，即有 $ n $ 个特征，共有 $ m $ 个样本。我们对高斯分布的参数 $ \mu , \Sigma $ 进行参数估计：

\[\mu = \frac{1}{m} \sum_{i=1}^m x^{(i)} \]

\[\Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)} - \mu)(x^{(i)} - \mu)^T \]

以上是基于矩阵的计算，其中

\[x^{(i)} = \begin{bmatrix} x_1^{(i)} \\ x_2^{(i)} \\ \vdots \\ x_n^{(i)} \\ \end{bmatrix} \mu = \begin{bmatrix} \mu_1 \\ \mu_2 \\ \vdots \\ \mu_n \\ \end{bmatrix} \]

3.3 基于多元高斯分布的异常检测

  具体步骤如下：
  （1）使用训练集拟合参数： $ \mu, \Sigma $

\[\mu = \frac{1}{m} \sum_{i=1}^m x^{(i)} \]

\[\Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)} - \mu)(x^{(i)} - \mu)^T \]

其中 $ i=1,2,...,m $ 为样本数，共有 $ n $ 个特征。
  （2）给定新样本 $ x $ ,计算 $ P(x) $

\[P(x) = P(x; \mu ,\Sigma ) = \frac{1}{(2 \pi)^{\frac{n}{2}} |\Sigma|^{\frac{1}{2}}} exp(-\frac{1}{2} (x- \mu)^T \Sigma^{-1} (x- \mu)) \]

  （3）若 $ P(x) < \epsilon $ 则判断为异常点。

3.4 简单高斯分布模型 v.s. 多元高斯分布模型

---

引用及参考：
[1] 《Machine Learning》Andrew Ng
[2] https://blog.csdn.net/u012328159/article/details/51462942
[3] https://blog.csdn.net/whuhan2013/article/details/53688915

写在最后：本文参考以上资料进行整合与总结，属于原创，文章中可能出现理解不当的地方，若有所见解或异议可在下方评论，谢谢！
若需转载请注明：https://www.cnblogs.com/lliuye/p/9174453.html