kmeans算法理解及代码实现

github：kmeans代码实现1、kmeans代码实现2(包含二分k-means)
本文算法均使用python3实现

---

1 聚类算法

  对于"监督学习"(supervised learning)，其训练样本是带有标记信息的，并且监督学习的目的是：对带有标记的数据集进行模型学习，从而便于对新的样本进行分类。而在“无监督学习”(unsupervised learning)中，训练样本的标记信息是未知的，目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律，为进一步的数据分析提供基础。对于无监督学习，应用最广的便是"聚类"(clustering)。
  “聚类算法”试图将数据集中的样本划分为若干个通常是不相交的子集，每个子集称为一个“簇”(cluster)，通过这样的划分，每个簇可能对应于一些潜在的概念或类别。
  我们可以通过下面这个图来理解：

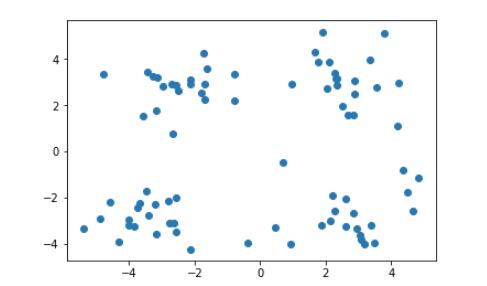
  上图是未做标记的样本集，通过他们的分布，我们很容易对上图中的样本做出以下几种划分。
  当需要将其划分为两个簇时，即 $ k=2 $ 时：

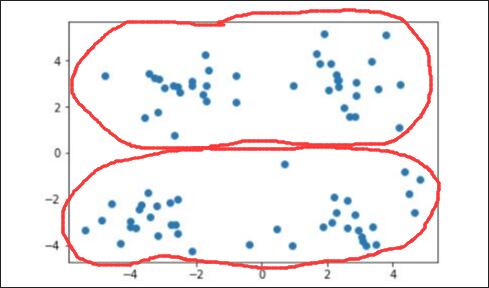
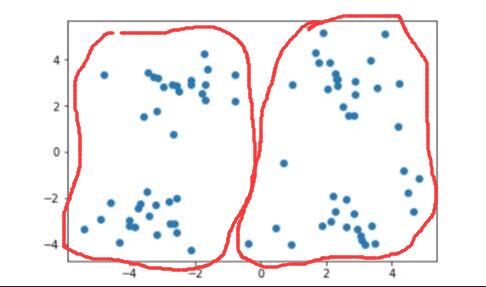
  当需要将其划分为四个簇时，即 $ k=4 $ 时：

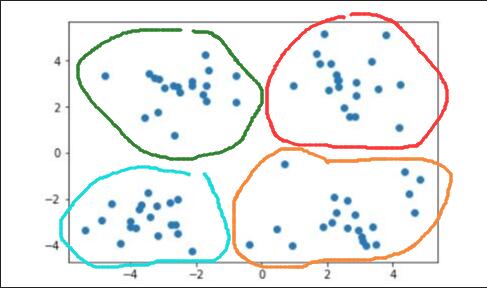
  那么计算机是如何进行这样的划分的呢？这就需要聚类算法来进行实现了。本文主要针对聚类算法中的一种——kmeans算法进行介绍。

---

2 kmeans算法

  kmeans算法又名k均值算法。其算法思想大致为：先从样本集中随机选取 $ k $ 个样本作为簇中心，并计算所有样本与这 $ k $ 个“簇中心”的距离，对于每一个样本，将其划分到与其距离最近的“簇中心”所在的簇中，对于新的簇计算各个簇的新的“簇中心”。
  根据以上描述，我们大致可以猜测到实现kmeans算法的主要三点：
  （1）簇个数 $ k $ 的选择
  （2）各个样本点到“簇中心”的距离
  （3）根据新划分的簇，更新“簇中心”

2.1 kmeans算法要点

  （1） $ k $ 值的选择
     $ k $ 的选择一般是按照实际需求进行决定，或在实现算法时直接给定 $ k $ 值。
  （2） 距离的度量
     给定样本 $ x^{(i)} = \lbrace x_1^{(i)},x_2,,...,x_n^{(i)}, \rbrace 与 x^{(j)} = \lbrace x_1^{(j)},x_2,,...,x_n^{(j)}, \rbrace ，其中 i,j=1,2,...,m，表示样本数，n表示特征数 $ 。距离的度量方法主要分为以下几种：
    （2.1）有序属性距离度量（离散属性 $ \lbrace1,2,3 \rbrace $ 或连续属性）：
      闵可夫斯基距离(Minkowski distance)：

\[dist_{mk}(x^{(i)},x^{(j)})=(\sum_{u=1}^n |x_u^{(i)}-x_u^{(j)}|^p)^{\frac{1}{p}} \]

      欧氏距离(Euclidean distance)，即当 $ p=2 $ 时的闵可夫斯基距离：

\[dist_{ed}(x^{(i)},x^{(j)})=||x^{(i)}-x^{(j)}||_2=\sqrt{\sum_{u=1}^n |x_u^{(i)}-x_u^{(j)}|^2} \]

      曼哈顿距离(Manhattan distance)，即当 $ p=1 $ 时的闵可夫斯基距离：

\[dist_{man}(x^{(i)},x^{(j)})=||x^{(i)}-x^{(j)}||_1=\sum_{u=1}^n |x_u^{(i)}-x_u^{(j)}| \]

    （2.2）无序属性距离度量（比如{飞机，火车，轮船}）：
      VDM(Value Difference Metric)：

\[VDM_p(x_u^{(i)},x_u^{(j)}) = \sum_{z=1}^k \left|\frac{m_{u,x_u^{(i)},z}}{m_{u,x_u^{(i)}}} - \frac{m_{u,x_u^{(j)},z}}{m_{u,x_u^{(j)}}} \right|^p \]

      其中 $ m_{u,x_u^{(i)}} $ 表示在属性 $ u $ 上取值为 $ x_u^{(i)} $ 的样本数， $ m_{u,x_u^{(i)},z} $ 表示在第 $ z $ 个样本簇中属性 $ u $ 上取值为 $ x_u^{(i)} $ 的样本数， $ VDM_p(x_u^{(i)},x_u) $ 表示在属性 $ u $ 上两个离散值 $ x_u^{(i)} 与 x_u^{(i)} $ 的 $ VDM $ 距离 。
    （2.3）混合属性距离度量，即为有序与无序的结合：

\[MinkovDM_p(x^{(i)},x^{(j)}) = \left( \sum_{u=1}^{n_c} | x_u^{(i)} - x_u^{(j)} | ^p + \sum_{u=n_c +1}^n VDM_p (x_u^{(i)},x_u^{(j)}) \right) ^{\frac{1}{p}} \]

      其中含有 $ n_c $ 个有序属性，与 $ n-n_c $ 个无序属性。
    本文数据集为连续属性，因此代码中主要以欧式距离进行距离的度量计算。
  （3） 更新“簇中心”
     对于划分好的各个簇，计算各个簇中的样本点均值，将其均值作为新的簇中心。

2.2 kmeans算法过程

---

  输入：训练数据集 $ D ={x^{(1)},x,...,x^{(m)}}$ ,聚类簇数 $ k $ ;
  过程：函数 $ kMeans(D, k, maxIter) $ .
  1：从 $ D $ 中随机选择 $ k $ 个样本作为初始“簇中心”向量： $ {\mu^{(1)},\mu,...,,\mu^{(k)}} $ :
  2：repeat
  3：  令 $ C_i = \emptyset (1 \leq i \leq k ) $
  4：  for $ j= 1,2,...,m $ do
  5：    计算样本 $ x^{(j)} $ 与各“簇中心”向量 $ \mu^{(i)} (1 \leq i \leq k ) $ 的欧式距离
  6：    根据距离最近的“簇中心”向量确定 $ x^{(j)} $ 的簇标记： $ \lambda_j = argmin_{i \in \lbrace 1,2,...,k \rbrace}d_{ji} $
  7：    将样本 $ x^{(j)} $ 划入相应的簇： $ C_{\lambda_j} = C_{\lambda_j} \bigcup \lbrace x^{(j)} \rbrace $ ;
  8：  end for
  9：  for $ i= 1,2,...,k $ do
  10：    计算新“簇中心”向量： $ (\mu^{(i)})' = \frac{1}{|C_i|} \sum_{x \in C_i}x $ ;
  11：    if $ (\mu^{(i)})' = \mu^{(i)} $ then
  12：      将当前“簇中心”向量 $ \mu^{(i)} $ 更新为 $ (\mu^{(i)})' $
  13：    else
  14：      保持当前均值向量不变
  15：    end if
  16：  end for
  17：  else
  18：until 当前“簇中心”向量均未更新
  输出：簇划分 $ C={C_1,C_2,...,C_K} $

---

  为避免运行时间过长，通常设置一个最大运行轮数或最小调整幅度阈值，若达到最大轮数或调整幅度小于阈值，则停止运行。
  过程如下图：

2.2 kmeans算法分析

  kmeans算法由于初始“簇中心”点是随机选取的，因此最终求得的簇的划分与随机选取的“簇中心”有关，也就是说，可能会造成多种 $ k $ 个簇的划分情况。这是因为kmeans算法收敛到了局部最小值，而非全局最小值。

---

3 二分k-means算法

  基于kmeans算法容易使得结果为局部最小值而非全局最小值这一缺陷，对算法加以改进。使用一种用于度量聚类效果的指标SSE(Sum of Squared Error)，即对于第 $ i $ 个簇，其SSE为各个样本点到“簇中心”点的距离的平方的和，SSE值越小表示数据点越接近于它们的“簇中心”点，聚类效果也就越好。以此作为划分簇的标准。
  算法思想是：先将整个样本集作为一个簇，该“簇中心”点向量为所有样本点的均值，计算此时的SSE。若此时簇个数小于 $ k $ ，对每一个簇进行kmeans聚类($ k=2 $) ，计算将每一个簇一分为二后的总误差SSE，选择SSE最小的那个簇进行划分操作。

3.1 kmeans算法过程

---

  输入：训练数据集 $ D ={x^{(1)},x,...,x^{(m)}}$ ,聚类簇数 $ k $ ;
  过程：函数 $ kMeans(D, k, maxIter) $ .
  1：将所有点看做一个簇，计算此时“簇中心”向量：$ \mu^{(1)} = \frac{1}{m} \sum_{x \in D}x $
  2：while $ “簇中心”个数h < k $ ：
  3：  for $ i= 1,2,...,h $ do
  4：    将第 $ i $ 个簇使用 kmeans算法进行划分，其中 $ k = 2 $
  5：    计算划分后的误差平方和 $ SSE_i $
  5：  比较 $ k $ 种划分的SSE值，选择SSE值最小的那种簇划分进行划分
  5：  更新簇的分配结果
  5：  添加新的“簇中心”
  18：until 当前“簇中心”个数达到 $ k $
  输出：簇划分 $ C={C_1,C_2,...,C_K} $

---

3.2 二分k-means算法分析

  二分k-means算法不再随机选取簇中心，而是从一个簇出发，根据聚类效果度量指标SSE来判断下一步应该对哪一个簇进行划分，因此该方法不会收敛到局部最小值，而是收敛到全局最小值。

---

引用及参考：
[1]《机器学习》周志华著
[2]《机器学习实战》Peter Harrington著
[3]https://blog.csdn.net/google19890102/article/details/26149927

写在最后：本文参考以上资料进行整合与总结，属于原创，文章中可能出现理解不当的地方，若有所见解或异议可在下方评论，谢谢！
若需转载请注明：https://www.cnblogs.com/lliuye/p/9144312.html