逻辑回归理解及代码实现

github：代码实现之逻辑回归
本文算法均使用python3实现

---

1. 什么是逻辑回归

《机器学习实战》一书中提到：

利用逻辑回归进行分类的主要思想是：根据现有数据对分类边界线建立回归公式，以此进行分类（主要用于解决二分类问题）。

由以上描述我们大概可以想到，对于使用逻辑回归进行分类，我们首先所需要解决的就是寻找分类边界线。那么什么是分类边界线呢？

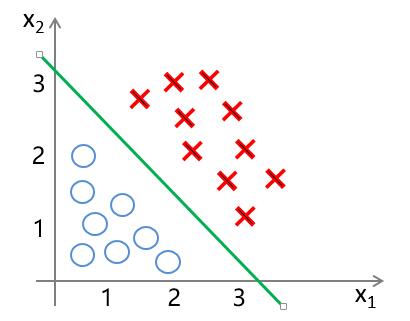
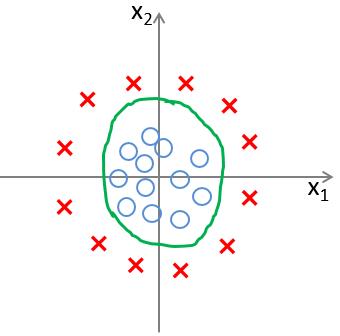
以上两幅图分别对应着，当分类样本具有两个特征值 $ x_1, x_2 $ 时，样本可进行线性可分，以及非线性可分的情况。而分类边界，便是图中所示的绿色直线与绿色曲线。（本文中只针对线性可分且特征数为 $ n $ 的情况进行介绍）
而使用逻辑回归进行分类，就是要找到这样的分类边界，使其能够尽可能地对样本进行正确分类，也就是能够尽可能地将两种样本分隔开来。于是我们可以大胆猜测，可以构造这样一个函数（图一中特征数为2，分类边界为直线，当特征数为 $ n $ 时分类边界为“超平面”），来对样本集进行分隔：

\[z(x^{(i)}) = \theta_0 + \theta_1 x^{(i)}_1 + \theta_2 x^{(i)}_2 + ... + \theta_n x^{(i)}_n \]

其中 $ i=1,2,...m $ ，表示第 $ i $ 个样本, $ n $ 表示特征数,当 $ z(x^{(i)}) > 0 $ 时，对应着样本点位于分界线上方，可将其分为"1"类；当 $ z(x^{(i)}) < 0 $ 时 ，样本点位于分界线下方，将其分为“0”类。
我们很容易联想到前面介绍过的线性回归，该算法同样是构造函数 $ h_\theta(x^{(i)}) = \theta_0 + \theta_1 x^{(i)}_1 + \theta_2 x^{(i)}_2 + ... + \theta_n x^{(i)}_n $ ，但与逻辑回归不同的是，线性回归模型输入一个待预测样本的特征值 $ x^{(i)}=[ x^{(i)}_1,x_2,...,x^{(i)}_n ]^T $ ，输出则为预测值。而逻辑回归作为分类算法，它的输出是0/1。那么如何将输出值转换成0/1呢？在此介绍一下 $ sigmoid $ 函数。

1.1 $ sigmoid $ 函数

   $ sigmoid $ 函数定义如下：

\[g(z) = \frac{1}{1+e^{-z}} \]

  其函数图像为：

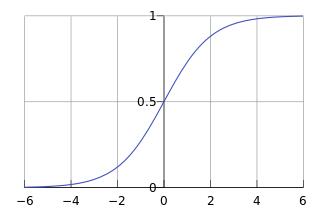
由函数图像可以看出， $ sigmoid $ 函数可以很好地将 $ (-\infty , \infty) $ 内的数映射到 $ (0 , 1) $ 上。于是我们可以将 $ g(z)\geq0.5 $ 时分为"1"类， $ g(z)<0.5 $ 时分为"0"类。即：

\[y = \begin{cases} 1, & \text {if $g(z) \geq 0.5$ } \\ 0, & \text{otherwise} \end{cases} \]

其中 $ y $ 表示分类结果。$ sigmoid $ 函数实际表达的是将样本分为“1”类的概率，这将在本文的最后一部分进行详细解释。

---

2. 逻辑回归模型函数

在了解了分类边界：

\[z(x^{(i)}) = \theta_0 + \theta_1 x^{(i)}_1 + \theta_2 x^{(i)}_2 = \theta^T x^{(i)} \]

  其中，

\[\theta = \begin{bmatrix} \theta_0 \\ \theta_1 \\ \theta_2 \\ \vdots \\ \theta_n \\ \end{bmatrix} ， x^{(i)} = \begin{bmatrix} x^{(i)}_0 \\ x^{(i)}_1 \\ x^{(i)}_2 \\ \vdots \\x^{(i)}_n \\ \end{bmatrix} \]

而 $ x_0^{(i)} = 1 $ 是偏置项（具体解释见线性回归）, $ n $ 表示特征数，$ i=1,2,...,m $ 表示样本数。
以及 $ sigmoid $ 函数 ：

\[g(z) = \frac{1}{1+e^{-z}} \]

我们可以构造出逻辑回归模型函数：

\[h_\theta(x^{(i)}) = g(z) = g( \theta^T x^{(i)} ) = \frac{1}{1+e^{-\theta^T x^{i}}} \]

使得我们可以对于新样本

\[x^{new} = [x^{new}_1, x^{new}_2,...,x^{new}_n]^T \]

进行输入，得到函数值 $ h_\theta(x^{new}) $ , 根据 $ h_\theta(x^{new}) $ 与0.5的比较来将新样本进行分类。

---

3. 逻辑回归代价函数

回想在线性回归中，我们是利用均方误差来作为代价函数：

\[J(\theta) = \frac{1}{2m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 \]

同样的，假设我们仍旧使用均方误差来作为逻辑回归大家函数，会出现什么效果呢？将 $ g(z) = \frac{1}{1+e^{-z}} $ 带入上式，我们会发现， $ J(\theta) $ 为一个非凸函数，也就是说该函数存在许多局部最小值点，在求解参数的过程中很容易陷入局部最小值点，而无法求得真正的最小值点。

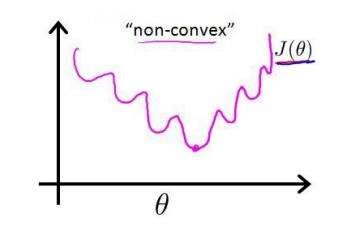
我们不妨换一个思路来求解这个问题。在上一节中提到：$ sigmoid $ 函数实际表达的是将样本分为“1”类的概率，也就是说，使用 $ sigmoid $ 函数求解出来的值为类1的后验估计 $ p(y=1|x,\theta) $ ,故我们可以得到：

\[p(y=1|x,\theta) = h_\theta(\theta^T x) \]

则

\[p(y=0|x,\theta) = 1- h_\theta(\theta^T x) \]

其中 $ p(y=1|x,\theta) $ 表示样本分类为 $ y=1 $ 的概率，而 $ p(y=0|x,\theta) $ 表示样本分类为 $ y=0 $ 的概率。针对以上二式，我们可将其整理为：

\[p(y|x,\theta)=p(y=1|x,\theta)^y p(y=0|x,\theta)^{(1-y)} = h_\theta(\theta^T x)^y (1- h_\theta(\theta^T x))^{(1-y)} \]

我们可以得到其似然函数为：

\[L(\theta) = \prod^m_{i=1} p(y^{(i)}|x^{(i)},\theta) = \prod ^m_{i=1}[ h_\theta(\theta^T x^{(i)})^{y^{(i)}} (1- h_\theta(\theta^T x^{(i)}))^{1-y^{(i)}}] \]

对数似然函数为：

\[\log L(\theta) = \sum_{i=1}^m [y^{(i)} \log{h_\theta(\theta^T x^{(i)})} +(1-y^{(i)}) \log{(1- h_\theta(\theta^T x^{(i)}))}] \]

于是，我们便得到了代价函数，我们可以对求 $ \log L(\theta) $ 的最大值来求得参数 $ \theta $ 的值。为了便于计算，将代价函数做了以下改变：

\[J(\theta) = - \frac{1}{m} \sum_{i=1}^m [y^{(i)} \log{h_\theta(\theta^T x^{(i)})} + (1-y^{(i)}) \log{(1- h_\theta(\theta^T x^{(i)}))}] \]

此时，我们只需对 $ J(\theta) $ 求最小值，便得可以得到参数 $ \theta $。
本节中逻辑回归代价函数是利用极大似然法进行的推导

---

4. 优化算法

对于以上所求得的代价函数，我们采用梯度下降的方法来求得最优参数。

3.1 梯度下降法(gradient descent)

梯度下降法过程为：
repeat {
$ \theta_j := \theta_j - \alpha \frac{\Delta J(\theta)}{\Delta \theta_j} $
}
其中 $ \alpha $ 为学习率（learning rate），也就是每一次的“步长”； $ \frac{\Delta J(\theta)}{\Delta \theta_j} $ 是梯度，$ j = 1,2,...,n $ 。
接下来我们对梯度进行求解：

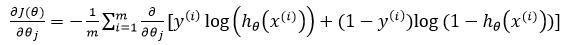
其中：

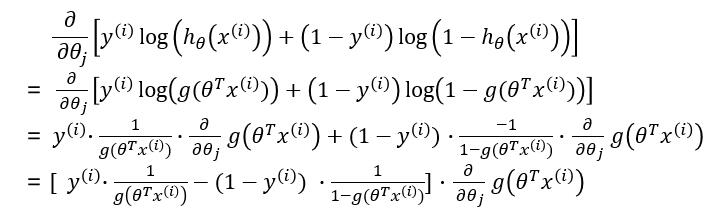
而又因为：

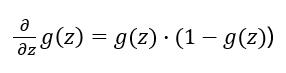
则：

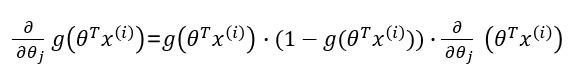
因此：

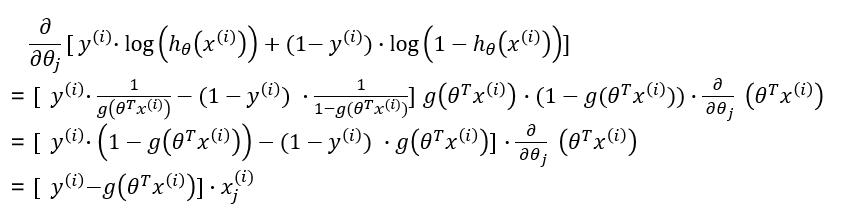
故：

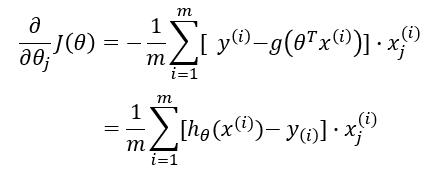
由以上我们可以得到梯度下降过程为：
repeat {
$ \theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^m (h_{\theta}(x^{(i)}) - y^{(i)}) \cdot x_j^{(i)} $
}
其中 $ i = 1,2,...,m，表示样本数 ; j = 1,2,..,n，表示特征数 $
通过观察我们可以发现，逻辑回归梯度下降中参数的更新公式同线性回归的一样。

---

5. 理解sigmoid函数

二项逻辑斯蒂回归模型(binomial logistic regression model)是一种分类模型，由条件概率分布 $ p(Y|X) $ 表示，形式为参数化的逻辑斯蒂分布。这里，随机变量 $ X $ 取值为实数，随机变量 $ Y $ 取值为 $ 1或0 $。可通过监督学习的方法来估计模型参数。
二项逻辑斯蒂回归模型是如下的条件概率分布：

\[p(Y=1|x) = \frac{e^{\theta^Tx}}{1+e^{\theta^Tx}} \]

\[p(Y=0|x) = \frac{1}{1+e^{\theta^Tx}} \]

其中， $ x \in R^n $ 是输入， $ Y \in \lbrace 0,1 \rbrace $ 是输出， $ \theta $ 是参数。
对于 $ Y=1 $ ：

\[p(Y=1|x) = \frac{e^{\theta^Tx}}{1+e^{\theta^Tx}} \]

而 $ e^{\thetaTx} \neq 0 $ ，故上式可推导为：

\[p(Y=1|x) = \frac{1}{1+e^{-\theta^Tx}} \]

即逻辑回归模型函数：

\[h_\theta(x^{(i)}) = \frac{1}{1+e^{-\theta^Tx^{(i)}}} \]

表示为分类结果为“1”的概率

---

引用及参考：
[1]《统计学方法》李航著
[2]《机器学习实战》Peter Harrington著
[3] https://blog.csdn.net/zjuPeco/article/details/77165974
[4] https://blog.csdn.net/ligang_csdn/article/details/53838743

写在最后：本文参考以上资料进行整合与总结，属于原创，文章中可能出现理解不当的地方，若有所见解或异议可在下方评论，谢谢！
若需转载请注明：https://www.cnblogs.com/lliuye/p/9129493.html