OpenGL学习脚印：深度測试(depth testing)

写在前面
上一节我们使用AssImp载入了3d模型，效果已经令人激动了。可是绘制效率和场景真实感还存在不足，接下来我们还是要保持耐心，继续学习一些高级主题，等学完后面的高级主题，我们再次来改进我们载入模型的过程。

本节将会学习深度測试。文中演示样例程序源码均能够在我的github下载。

本节内容整理自
1.www.learnopengl.com Depth testing
2.depth buffer faq
3.Z buffer 和 W buffer 簡介

通过本节能够了解到

• 为什么须要深度缓冲区？
• OpenGL中怎么使用深度缓冲区 ？
• 可视化深度值
• 深度值的精度问题-ZFighting

问题背景

在绘制3D场景的时候，我们须要决定哪些部分对观察者是可见的。或者说哪些部分对观察者不可见，对于不可见的部分，我们应该及早的丢弃，比如在一个不透明的墙壁后的物体就不应该渲染。这样的问题称之为隐藏面消除（Hidden surface elimination）,或者称之为找出可见面(Visible surface detemination)。

解决这一问题比較简单的做法是画家算法(painter’s algorithm)。

画家算法的基本思路是，先绘制场景中离观察者较远的物体，再绘制较近的物体。

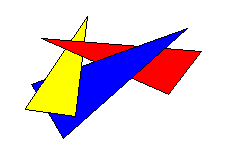
比如绘制以下图中的物体(来自Z buffer 和 W buffer 簡介)。先绘制红色部分，再绘制黄色，最后绘制灰色部分。就可以解决隐藏面消除问题。

使用画家算法时。仅仅要将场景中物体依照离观察者的距离远近排序，由远及近的绘制就可以。画家算法非常easy，但还有一方面也存在缺陷，比如以下的图中，三个三角形互相重叠的情况。画家算法将无法处理：

解决隐藏面消除问题的算法有非常多，详细能够參考Visible Surface Detection。结合OpenGL，我们使用的是Z-buffer方法，也叫深度缓冲区Depth-buffer。

深度缓冲区(Detph buffer)同颜色缓冲区(color buffer)是相应的。颜色缓冲区存储的像素的颜色信息，而深度缓冲区存储像素的深度信息。在决定是否绘制一个物体的表面时，首先将表面相应像素的深度值与当前深度缓冲区中的值进行比較，假设大于等于深度缓冲区中值，则丢弃这部分;否则利用这个像素相应的深度值和颜色值。分别更新深度缓冲区和颜色缓冲区。

这一过程称之为深度測试(Depth Testing)。

在OpenGL中运行深度測试时，我们能够依据须要指定深度值的比較函数。后面会详细介绍详细使用。

OpenGL中使用深度測试

深度缓冲区一般由窗体管理系统，比如GLFW来创建。深度值一般由16位，24位或者32位值表示，一般是24位。位数越高的话，深度的准确度越好。

前面我们已经见过了怎样在OpenGL中使用深度測试，这里复习下过程。首先我们须要开启深度測试，默认是关闭的：

   glEnable(GL_DEPTH_TEST);

另外还须要在绘制场景前。清除颜色缓冲区时。清除深度缓冲区：

   glClearColor(0.18f, 0.04f, 0.14f, 1.0f);
   glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

清除深度缓冲区的默认值是1.0，表示最大的深度值，深度值的范围在[0,1]之间，值越小表示越靠近观察者，值越大表示远离观察者。
上面提到了在进行深度測试时，当前深度值和深度缓冲区中的深度值，进行比較的函数，能够由用户通过glDepthFunc指定，这个函数包含一个參数，详细的參数例如以下表所看到的：

函数	说明
GL_ALWAYS	总是通过測试
GL_NEVER	总是不通过測试
GL_LESS	在当前深度值 < 存储的深度值时通过
GL_EQUAL	在当前深度值 = 存储的深度值时通过
GL_LEQUAL	在当前深度值 <= 存储的深度值时通过
GL_GREATER	在当前深度值 > 存储的深度值时通过
GL_NOTEQUAL	在当前深度值 不等于 存储的深度值时通过
GL_GEQUAL	在当前深度值 >= 存储的深度值时通过

比如我们能够使用GL_AWALYS參数，这与默认不开启深度測试效果是一样的：

  glDepthFunc(GL_ALWAYS);

以下我们绘制两个立方体和一个平面，通过对照开启和关闭深度測试来理解深度測试。
当关闭深度測试时，我们得到的效果却是这样的：

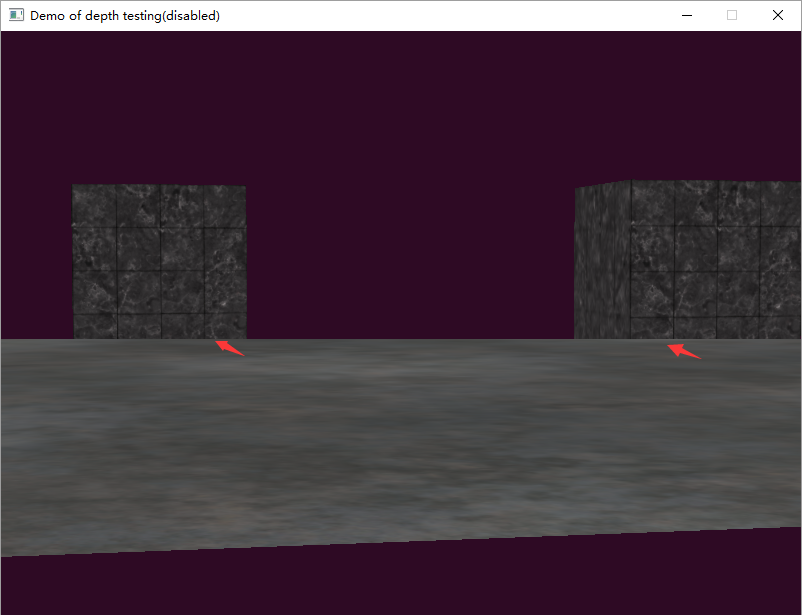
这里先绘制立方体。然后绘制平面，假设关闭深度測试，OpenGL仅仅依据绘制的先后顺序决定显示结果。那么后绘制的平面遮挡了一部分先绘制的本应该显示出来的立方体。这样的效果是不符合实际的。

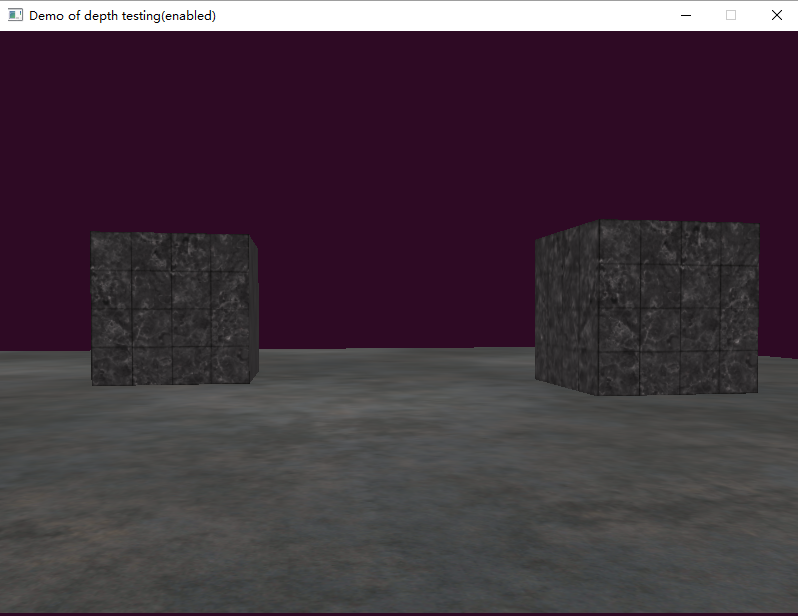
我们开启深度測试后绘制场景，得到正常的效果例如以下：

使用深度測试。最常见的错误时没有使用glEnable(GL_DEPTH_TEST);
开启深度測试。或者没有使用glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);清除深度缓冲区。

与深度缓冲区相关的还有一个函数是glDepthMask,它的參数是布尔类型，GL_FALSE将关闭缓冲区写入。默认是GL_TRUE，开启了深度缓冲区写入。

可视化深度值

在可视化深度值之前，首先我们要明确，这里的深度值，实际上是屏幕坐标系下的zwin坐标。屏幕坐标系下的(x,y)坐标分别表示屏幕坐标系下以左下角(0,0)为起始点的坐标。

zwin我们怎样获取呢？ 能够通过着色器的输入变量gl_FragCoord.z来获取。这个gl_FragCoord的z坐标表示的就是深度值。

我们在着色器中以这个深度值为颜色输出：

  // 原样输出
float asDepth()
{
  return gl_FragCoord.z;
}
void main()
{
    float depth = asDepth();
    color = vec4(vec3(depth), 1.0f);
}

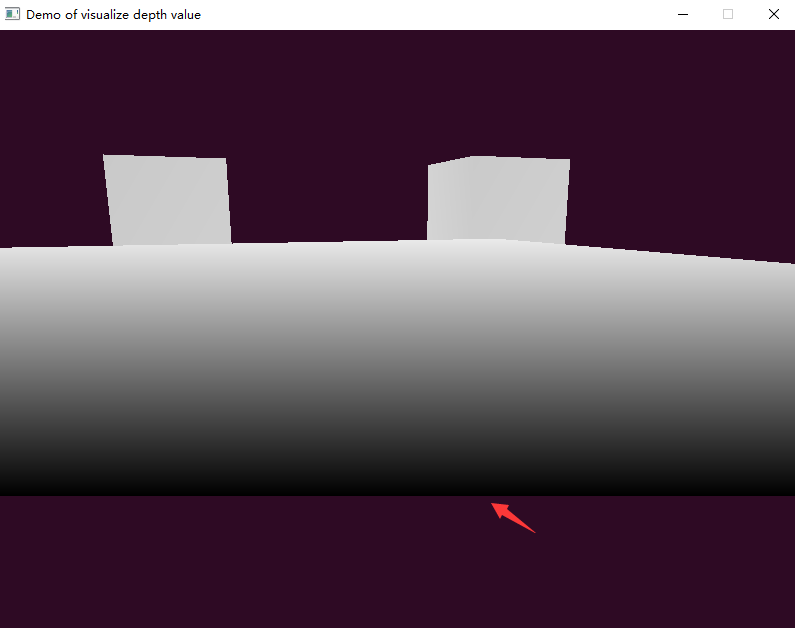
输出后的效果例如以下图所看到的：

能够看到图中，仅仅有离观察者较近的部分有些黑色。其余的都是白色。这是由于深度值zwin和zeye是成非线性关系的，在离观察者近的地方，准确度较高，zwin值都保持在较小范围。成黑色。

可是一旦超出一定距离。准确度变小，zwin值都挤在1.0附近。因此成白色。当我们向后移动，拉远场景与观察者的距离后，zwin值都落在1.0附近，整个场景都变成白色。例如以下图所看到的：

作为深度值的可视化，我们能不能使用线性的关系来表达zwin和zeye ? 这里我们做一个尝试，从zwin反向推导出z_{eye}$。在投影矩阵和视口变换矩阵一节。我们计算出了相机坐标系下坐标和规范化设备坐标系下坐标之间的关系例如以下：

zndc=−f+nf−nzeye−2fnf−n−zeye=f+nf−n+2fn(f−n)zeye(1)

在OpenGL中从规范化设备坐标系转换到屏幕坐标系使用函数主要是：
glViewport(GLint sx , GLint sy , GLsizei ws , GLsizei hs);
glDepthRangef(GLclampf ns , GLclampf fs );

继而能够得到规范化设备坐标系和屏幕设备坐标系之间的关系例如以下：

zwin=fs−ns2zndc+fs+ns2(2)

默认情况下glDepthRange函数的n=0,f=1,因此从（2）式能够得到：
zwin=12zndc+12(3)
zndc=2zwin−1(4)

从式子（1）我们能够得到：
zeye=2fnzndc(f−n)−(f+n)(5)

上面的式子(5)假设用来作为深度值，由于结果是负数，会被截断到0.0，结果都是黑色。因此我们对分母进行反转。写为式子(6)作为深度值。

zeye=2fn(f+n)−zndc(f−n)(6)

对式子(6)的深度值进行归一化，保持在[0,1]范围内，则在着色器中实现为：

// 线性输出结果
float near = 1.0f; 
float far  = 100.0f; 
float LinearizeDepth() 
{
    // 计算ndc坐标 这里默认glDepthRange(0,1)
    float Zndc = gl_FragCoord.z * 2.0 - 1.0; 
    // 这里分母进行了反转
    float Zeye = (2.0 * near * far) / (far + near - Zndc * (far - near)); 
    return (Zeye - near)/ ( far - near);
}
void main()
{
    float depth = LinearizeDepth();
    color = vec4(vec3(depth), 1.0f);
}

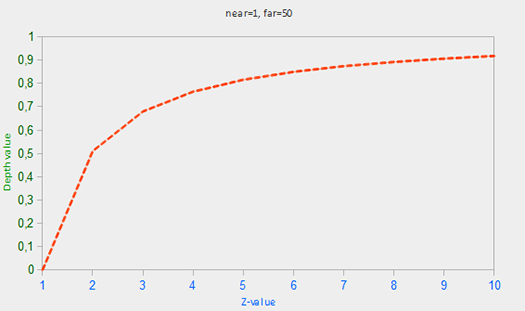
使用zwin和zeye线性关系得到深度值，绘制的效果例如以下图所看到的：

非常多网络教程都近似表达zwin和zeye的非线性关系，用来可视化，我们能够从(4)(6)得到非线性关系：
zwin=1n−1zeye1n−1f(7)
在着色器中实现为：

   // 非线性输出
float nonLinearDepth()
{
    float Zndc = gl_FragCoord.z * 2.0 - 1.0; 
    float Zeye = (2.0 * near * far) / (far + near - Zndc * (far - near)); 
    return (1.0 / near - 1.0 / Zeye) / (1.0 / near - 1.0 / far);
}
void main()
{
    float depth = nonLinearDepth();
    color = vec4(vec3(depth), 1.0f);
}

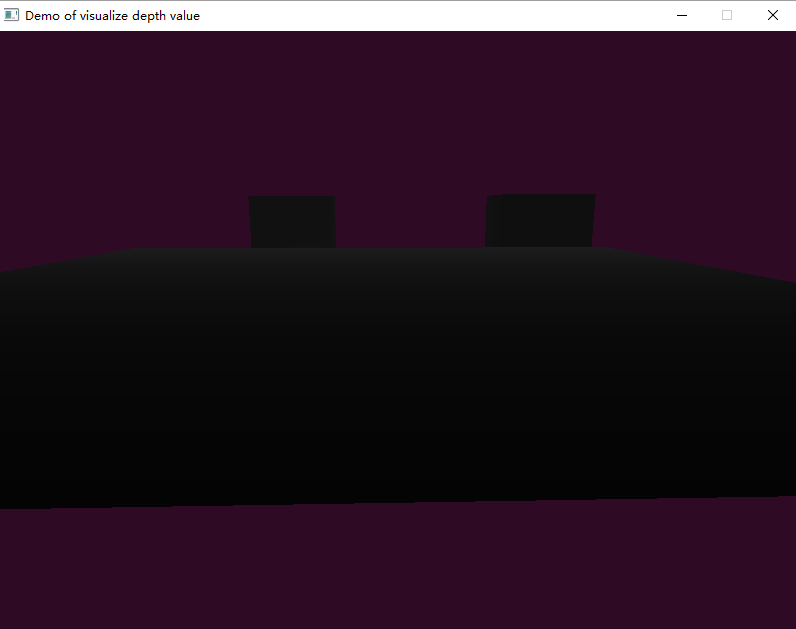
这个非线性关系输出。和利用gl_FragCoord.z作为深度值输出效果是几乎相同的。

深度的准确度问题-ZFighting

实际使用时不使用zwin和zeye的线性关系，由于在场景中，近处的物体，我们想让它看的清晰，自然 要求精度高；可是远处的物体。我们不须要非常清晰的看到细节，因此准确度不必和近处的物体一样。

使用公式(7)绘制的zwin和zeye关系图例如以下所看到的(来自：www.learnopengl.com Depth testing)：

我们看到。zeye在[1.0,2.0]范围内时zwin保持在0.5的范围内，准确度高。而当zeye超过10.0后，zwin的值就在0.9以后了。也就是说zwin在[10.0,50.0]范围内的深度值将挤在[0.9,1.0]这么一个小的范围内。准确度非常低。

实际上深度值是通过下式计算的(来自:depth buffer faq)：
zwin=S∗(fn(f−n)zeye+12f+nf−n+12)(8)
当中，S=2d−1，d表示深度缓冲区的位数(比如16,24,32)。

这个式子的右边括号部分是由(1)(4)得到，同一时候放大S倍数后得到终于的深度值(能够參看depth buffer faq)。

找到两个特殊点。zwin=1和zwin=S−1。得到：
zwin=1=>zeye=f∗n/((1/s)∗(f−n)−f)
zwin=S−1=>zeye=f∗n/(((s−1)/s)∗(f−n)−f)

取n = 0.01, f = 1000 and s = 65535。那么有：
zwin=1=>zeye=−0.01000015
zwin=S−1=>zeye=−395.90054

注意OpenGL中相机坐标系的+Z轴指向观察者，因此上面的坐标是负数。

从上面的值我们能够看到，当zeye在[-395,-1000]范围内时。深度值将所有挤在65534或者65535这两个值上，也就是说差点儿60%的zeye仅仅能分配1到2个深度值。可见当zeye超过一定范围后，精度值是相当低的。(这个样例原本解释来自depth buffer faq)。

当深度值准确度非常低时，easy引起ZFighting现象。表现为两个物体靠的非常近时确定谁在前，谁在后时出现了歧义。

比如上面绘制的平面和立方体，在y=-0.5的位置二者贴的非常近，假设进入立方体内部观察，则出现了ZFighting现象，立方体的底面纹理和平面的纹理出现了交错现象，例如以下图所看到的：

（假设你要亲自观察这个现象，仅仅须要在本节代码中。将相机位置放在立方体内部。略微调整鼠标观察角度就能够了）。

预防ZFighting的方法

1.不要将两个物体靠的太近，避免渲染时三角形叠在一起。这样的方式要求对场景中物体插入一个少量的偏移，那么就可能避免ZFighting现象。

比如上面的立方体和平面问题中，将平面下移0.001f就能够解决问题。当然手动去插入这个小的偏移是要付出代价的。
2.尽可能将近裁剪面设置得离观察者远一些。上面我们看到，在近裁剪平面附近，深度的准确度是非常高的，因此尽可能让近裁剪面远一些的话。会使整个裁剪范围内的准确度变高一些。可是这样的方式会使离观察者较近的物体被裁减掉，因此须要调试好裁剪面參数。
3.使用更高位数的深度缓冲区，通常使用的深度缓冲区是24位的，如今有一些硬件使用使用32位的缓冲区，使准确度得到提高。

当然还有其它方法，这里不再展开了。

最后的说明

本节了解了深度測试的问题背景，OpenGL中的用法。

通过可视化深度值和给出深度的计算过程，让我们了解深度的准确度问题。还有一些问题没有在本节探讨。包含gl_FragCoord,gl_FragDepth的含义和计算方法，等待后面再继续学习。另外关于fragment,pixel的差别还须要做进一步了解。本文关于这部分的表述还有待改善。

參考资料

1.www.learnopengl.com Depth testing
2.深度值计算 Real depth in OpenGL / GLSL
3.提供了深度值在线计算程序
4.opengl wiki Depth_Buffer_Precision
5.Z-buffering
6.上面提到的线性和非线性的计算方法 SO讨论