【CODEFORCES】 C. Dreamoon and Strings
Dreamoon has a string s and a pattern string p.
He first removes exactly x characters from s obtaining
string s' as a result. Then he calculates 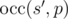 that
is defined as the maximal number of non-overlapping substrings equal to p that can be found in s'.
He wants to make this number as big as possible.
that
is defined as the maximal number of non-overlapping substrings equal to p that can be found in s'.
He wants to make this number as big as possible.
More formally, let's define 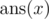 as
maximum value of
as
maximum value of 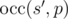 over
all s' that can be obtained by removing exactly x characters
from s. Dreamoon wants to know
over
all s' that can be obtained by removing exactly x characters
from s. Dreamoon wants to know 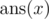 for
all x from 0 to |s| where |s| denotes
the length of string s.
for
all x from 0 to |s| where |s| denotes
the length of string s.
The first line of the input contains the string s (1 ≤ |s| ≤ 2 000).
The second line of the input contains the string p (1 ≤ |p| ≤ 500).
Both strings will only consist of lower case English letters.
Print |s| + 1 space-separated integers in a single line representing the 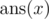 for
all x from 0 to |s|.
for
all x from 0 to |s|.
aaaaa aa
2 2 1 1 0 0
axbaxxb ab
0 1 1 2 1 1 0 0
For the first sample, the corresponding optimal values of s' after removal 0 through |s| = 5 characters from s are {"aaaaa", "aaaa","aaa", "aa", "a", ""}.
For the second sample, possible corresponding optimal values of s' are {"axbaxxb", "abaxxb", "axbab", "abab", "aba", "ab",
题解:这一题是DP。用D[i][j]表示从1至i。已经取走j个字符时的最大匹配串数。那么,第i位就有2种决策。取还是不取。而不取又分两种情况,一种是与前面的字符串没有能匹配的,一种是和前面的字符串有能匹配的。所以我们能够将状态转移方程表演示样例如以下:
D[i][j]=max(D[i-1][k-1],D[i-1][k]) //取还是不取
D[i][j]=max(D[i][j],D[k][j-(i-k-l2)]) //假设与前面有能匹配的情况
分析清楚了以后。能够发现这个问题跟最长不下降子序列事实上非常像。接下来就是编程实现了。要注意边界。D[i][j]的j不能大于i。并且不能为负数。
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
char s1[2005],s2[2005];
int l1,l2,j,d[2005][2005],f;
int mac(int i)
{
int x=i,y=l2;
while (x && y)
{
if (!y) break;
if (s1[x-1]==s2[y-1]) {x--; y--;}
else x--;
}
if (!y)
{
j=x;
return 1;
}
else
{
j=0;
return 0;
}
}
int main()
{
scanf("%s",s1);
scanf("%s",s2);
l1=strlen(s1);
l2=strlen(s2);
for (int i=1;i<=l1;i++)
{
f=mac(i);
for (int k=0;k<=i;k++)
{
d[i][k]=max(d[i-1][k],d[i-1][k-1]);
if (f && j>=k-i+j+l2 && k-i+j+l2>=0) d[i][k]=max(d[i][k],d[j][k-(i-j-l2)]+1);
}
}
for (int i=0;i<=l1;i++)
printf("%d ",d[l1][i]);
return 0;
}


