codeforce 571 B Minimization
题意:给出一个序列,经过合适的排序后。使得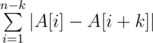 最小。
最小。
做法:将a升序排序后,dp[i][j]:选择i个数量为n/k的集合,选择j个数量为n/k+1的集合的最小值。
举个样例,
a={1,2,3,4,5,6,7,8,9,10},k=2
那么直接贪心可做,是这样。
1,x,2,x,3,x,4,x,5,x。(也就是1,2,3,4,5作为一个集合)
6 7 8 9 10(也就是6,7,8,9,10作为一个集合)
放在一起就是1,6。2。7。3,8,4。9,5,10。
若是k=3就要考虑长度为n/k+1=4的集合,是将1,2,3,4放在一起呢?还是4。5。6,7放在一起呢?就须要dp了。
dp[i+1][j]=min(dp[i+1][j],dp[i][j]+sb[x+sz-1]-sb[x]);
dp[i][j+1]=min(dp[i][j+1],dp[i][j]+sb[x+sz]-sb[x]);
x:当前还未考虑元素的最小下标
sb:一段连续元素差的和
#include<map>
#include<string>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<queue>
#include<vector>
#include<iostream>
#include<algorithm>
#include<bitset>
#include<climits>
#include<list>
#include<iomanip>
#include<stack>
#include<set>
using namespace std;
typedef long long ll;
int a[300010];
ll sb[3000010];
ll dp[5010][5010];
int main()
{
int n,k;
cin>>n>>k;
int sz=n/k;
for(int i=0;i<n;i++)
cin>>a[i];
sort(a,a+n);
for(int i=1;i<n;i++)
sb[i]=sb[i-1]+a[i]-a[i-1];
memset(dp,63,sizeof(dp));
dp[0][0]=0;
int m=n%k,len=k-m;
for(int i=0;i<=len;i++)
for(int j=0;j<=m;j++)
{
int x=(i+j)*sz+j;
dp[i+1][j]=min(dp[i+1][j],dp[i][j]+sb[x+sz-1]-sb[x]);
dp[i][j+1]=min(dp[i][j+1],dp[i][j]+sb[x+sz]-sb[x]);
}
cout<<dp[len][m];
}



