logistic回归和probit回归预测公司被ST的概率(应用)
1.适合阅读人群:
知道以下知识点:盒状图、假设检验、逻辑回归的理论、probit的理论、看过回归分析,了解AIC和BIC判别准则、能自己跑R语言程序
2.本文目的:用R语言演示一个相对完整的逻辑回归和probit回归建模过程,同时让自己复习一遍在学校时学的知识,记载下来,以后经常翻阅。
3.本文不涉及的部分:
(1)逻辑回归和probit回归参数估计的公式推导,在下一篇写;
(2)由ROC曲线带来的阈值选择,在下下一篇写;
(3)本文用的数据取自王汉生老师《应用商务统计分析》第四章里的数据,直接描述性分析和建模,没有涉及到数据预处理。
4.废话少说,上程序:
#适合人群:知道以下知识点:盒状图、假设检验、逻辑回归的理论、probit的理论、看过回归分析,了解AIC和BIC判别准则、能读R语言程序
1.#########读入数据##############
a=read.csv("C:/Users/Thinkpad/Desktop/ST.csv",header=T)
a1=a[a$year==1999,-1] #训练集
a2=a[a$year==2000,-1] #测试集
a1[c(1:5),]
2.####初步描述性分析######
boxplot(ARA~ST,data=a1,main="ARA") #画出各变量与ST的盒状图,初步查看因变量单独和各个解释性变量的关系
par(mfrow=c(3,2)) #只是初步的描述性分析,没有控制其他因素的影响,没有经过严格的统计检验
boxplot(ASSET~ST,data=a1,main="ASSET")
boxplot(ATO~ST,data=a1,main="ATO")
boxplot(GROWTH~ST,data=a1,main="GROWTH")
boxplot(LEV~ST,data=a1,main="LEV")
boxplot(ROA~ST,data=a1,main="ROA")
boxplot(SHARE~ST,data=a1,main="SHARE")
par(mfrow=c(1,1))
glm0.a=glm(ST~1,family=binomial(link=logit),data=a1) ####逻辑回归时:计算模型的整体显著性水平#####
glm1.a=glm(ST~ARA+ASSET+ATO+GROWTH+LEV+ROA+SHARE, #结果为7.4e-05,说明模型整体高度显著,也就是说所考虑的7个解释性变量中,至少有一个与因变量有关,具体哪一个不知道
family=binomial(link=logit),data=a1)
anova(glm0.a,glm1.a)
1-pchisq(30.565,7)
glm0.b=glm(ST~1,family=binomial(link=probit),data=a1) ####probit回归时:计算模型的整体显著性水平#####
glm1.b=glm(ST~ARA+ASSET+ATO+GROWTH+LEV+ROA+SHARE, #和逻辑回归结果一样,显著
family=binomial(link=probit),data=a1)
anova(glm0.b,glm1.b)
1-pchisq(31.702,7)
####看看是哪个自变量对因变量有影响#####
Anova(glm1.a,type="III") #对模型glm1.a做三型方差分析
summary(glm1.a)
Anova(glm1.b,type="III") #对模型glm1.b做三型方差分析
summary(glm1.b)
3.#######模型选择时要解决的问题:(1)选哪个模型;(2)选哪个阈值。
#######其中选6个中的哪个模型用ROC曲线确定(里面涉及到两个指标:TPR,FPR。至于为什么选择用这两个指标来衡量模型的好坏,请往下看,下面会解释,别着急),选择ROC曲线最上面的那条线所对应的模型。
#######模型确定之后,选取阈值可以根据ROC曲线和实际业务确定。(这里还需要查资料,至于什么ROC曲线,别急,继续向下看)
#######6个模型:逻辑回归的全模型,逻辑回归的AIC模型,逻辑回归的BIC模型,probit回归的全模型,probit回归的AIC模型,probit回归的BIC模型,
#我们先随便选两个模型感受一个AIC和BIC值
AIC(glm0.a) #计算逻辑回归方法时,空模型glm0.a的AIC取值
AIC(glm1.a) #计算逻辑回归方法时,全模型glm1.a的AIC取值
AIC(glm0.a,k=log(length(a1[,1]))) #计算逻辑回归方法时,空模型glm0.a的BIC取值
AIC(glm1.a,k=log(length(a1[,1]))) #计算逻辑回归方法时,全模型glm1.a的BIC取值
#上面只是比较了两个模型的AIC值,BIC值,我们有7个解释变量,一共会有128个不同模型,理论上说需要对这128个模型逐一研究,并选择最有模型,在R中
#我们可以自动的、尽量多的根据AIC搜索最优模型
logit.aic=step(glm1.a,trace=0) #根据AIC准则选择逻辑回归最优模型
summary(logit.aic)
n=length(a1[,1]) #根据BIC准则选择逻辑回归最优模型###
logit.bic=step(glm1.a,k=log(n),trace=0)
summary(logit.bic)
#上面AIC和BIC的结果有点差别,可以理解为AIC三个结果都很重要,而其中的ARA极其重要,BIC选择的模型更简单
#AIC选择的模型的预测精度似乎更好,我们老师当时也说要用AIC准则选模型
probit.aic=step(glm1.b,trace=0) #根据AIC准则选择probit回归最优模型,并赋值给probit.aic
summary(probit.aic)
probit.bic=step(glm1.b,k=log(n),trace=0) #根据bIC准则选择probit回归最优模型,并赋值给probit.bic
summary(probit.bic)
##############画出6个模型的ROC曲线来确定最终选哪一个模型################
p=matrix(0,length(a2[,1]),6) #生成矩阵,用于存储各模型的预测值
p[,1]=predict(glm1.a,a2)
p[,2]=predict(logit.aic,a2)
p[,3]=predict(logit.bic,a2)
p[,c(1:3)]=exp(p[,c(1:3)])/(1+exp(p[,c(1:3)])) #计算预测得到的概率
p[,4]=predict(glm1.b,a2)
p[,5]=predict(probit.aic,a2)
p[,6]=predict(probit.bic,a2)
p[,c(4:6)]=pnorm(p[,c(4:6)]) #计算预测得到的概率
plot(c(0,1),c(0,1),type="l",main="FPR vs. TPR",xlab="FPR",ylab="TPR") #画图,生成基本框架
FPR=rep(0,ngrids)
TPR=rep(0,ngrids)
for(k in 1:6){
prob=p[,k] #取出p中第K列的值,即第K个模型的预测概率
for(i in 1:ngrids){
p0=i/ngrids #选取阈值
ST.hat=1*(prob>p0) #根据阈值生成预测值
FPR[i]=sum((1-ST.true)*ST.hat)/sum(1-ST.true)
TPR[i]=sum(ST.true*ST.hat)/sum(ST.true)
}
points(FPR,TPR,type="b",col=k,lty=k,pch=k) #向图上添加第k个模型的TPR与FPR的散点图
}
legend(0.6,0.5,c("LOGIT FULL MODEL","LOGIT AIC MODEL",
"LOGIT BIC MODEL","PROBIT FULL MODEL","PROBIT AIC MODEL",
"PROBIT BIC MODEL"),lty=c(1:6),col=c(1:6),pch=c(1:6))
4.#########预测与评估,由ROC曲线,我们这里选择基于AIC准则的逻辑回归模型,阈值选择0.05,这块的选择还需要再查阅资料确定###########
p=predict(logit.aic,a2)
p=exp(p)/(1+exp(p))
a2$ST.pred=1*(p>0.05)
table(a2[,c(8,9)])
####对于每个个体,最终的预测结果为
a2$ST.pred
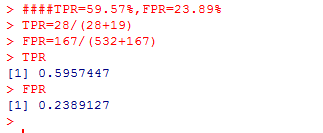
####TPR=59.57%,FPR=23.89%
TPR=28/(28+19)
FPR=167/(532+167)
#####################有一定基础的到这里就可以结束啦,感兴趣的还可以向下看##########################
##########下面我们随便选几个模型,来解释下为什么要使用TPR和FPR这两个指标衡量模型的精度,然后画出ROC曲线,提供逻辑回归全模型时,在众多不同的FPR下的TPR取值######################################
summary(glm1.a)
p=predict(glm1.a,a2) #利用逻辑回归的全模型glm1.a对数据a2进行预测
p=exp(p)/(1+exp(p)) #计算预测得到的概率
a2$ST.pred=1*(p>0.5) #以0.5为阈值生成预测值
table(a2[,c(8,9)])
###从结果看来,预测精度699/746=93.7%,没有正确预测一家ST公司
#####说明不能用总体精度来衡量预测的好坏,我们有可能犯两类错误:(1)把真实的ST公司预测为0;(2)把真实的非ST公司预测为1。由于我们关心的是找出那些ST公司
#####,可以通过下面两个指标来度量上面两种错误
#####TPR:把真实的ST公司正确地预测为ST=1的概率;
#####FPR:把真实的非ST公司错误地预测为ST=1的概率
#####上面预测TPR=0(很糟糕),FPR=0(非常好),下面我们把阈值改为0试试结果
a2$ST.pred=1*(p>0) #以0为阈值生成预测值,TPR=100%(非常好),FPR=100%(很糟糕)
table(a2[,c(8,9)])
######由结果可知这两个指标的取值是鱼和熊掌不可兼得
a2$ST.pred=1*(p>0.05) #以0.05为阈值生成预测值
table(a2[,c(8,9)]) #计算预测值与真实值的2维频数表
######上面一直说了ROC曲线,这里开始解释ROC曲线是何方神圣,上面说了FPR和TPR是鱼和熊掌不可兼得,那么现在我们便以FPR为横坐标,TPR为纵坐标,画出他们的曲线,看看他们究竟是什么关系,而这个曲线的名字就是ROC曲线
#########下面为了得到全面的分析,我们写了循环,以逻辑回归的全模型为例,提供在众多不同的FPR下的TPR取值
ngrids=100
TPR=rep(0,ngrids)
FPR=rep(0,ngrids)
p0=rep(0,ngrids)
for(i in 1:ngrids){
p0[i]=i/ngrids; #选取阈值p0
ST.true=a2$ST
ST.pred=1*(p>p0[i])
TPR[i]=sum(ST.pred*ST.true)/sum(ST.true)
FPR[i]=sum(ST.pred*(1-ST.true))/sum(1-ST.true)
}
plot(FPR,TPR,type="l",col=2) #画出FPR与TPR的散点图,即ROC曲线
points(c(0,1),c(0,1),type="l",lty=2) #添加对角线
5.结果:
图1 箱形图:用来观察哪个变量对因变量有影响
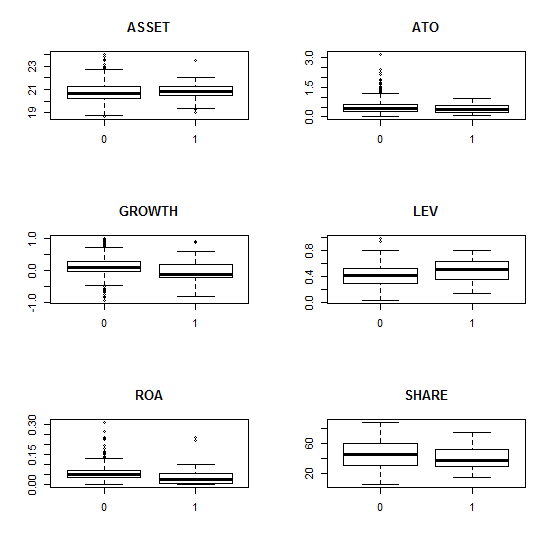
图2 ROC曲线:为了确定选择哪个模型以及作为阈值选择的初步参考
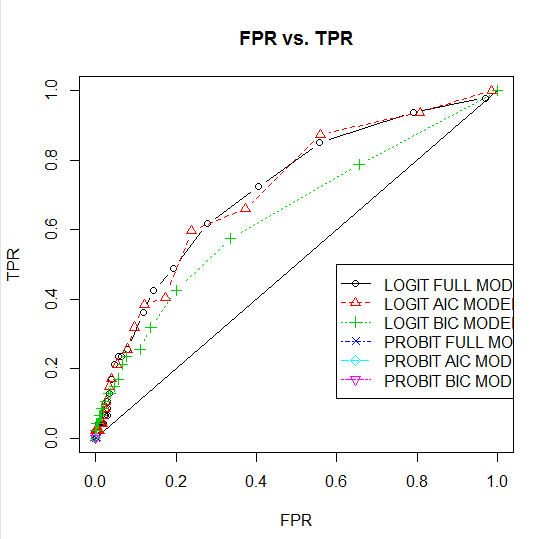
图3 预测结果:1:ST了,0:未被ST

图4 预测模型的精度
6.参考资料:
王汉生《应用商务统计分析》第四章。
end!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号