算法 - 比赛得分可能数
算法 - 比赛得分可能数
1 介绍
2 实现
2.1 分析
2.2 算法一
2.3 算法二
2.4 算法三
1 介绍
以排球比赛分例，默认情况下，A、B 两队比赛时，率先得到 25 分得将取胜。但若双方打成 24:24 时，则最高得分将变为 26 分。以后情况以此类推，例如，理论上可以打出诸如 40:42 这样的结局。
算法的要求是，在已知最终比分的情况下，算出能够达到该最终比分的所有可能得分顺序。
例1：如果最终比分是 0:25，那么只有一种顺序，那就是：
0:1 → 0:2 → 0:3 → ... 0:24 → 0:25
例2：如果最终比分是 1:25，那么可能有 25 种情况，例如：
1:0 → 0:1 → 0:2 → 0:3 → ... 0:24 → 0:25
0:1 → 1:1 → 1:2 → 1:3 → ... 1:24 → 1:25
0:1 → 0:2 → 1:2 → 1:3 → ... 1:24 → 1:25
......
例3：如果最终比分是 3:25，将有 2925 种情况
例4：如果最终比分是 3：12，结果为 0，因为不可能有这种情况的最终比分
要求编写程序实现该功能，可以支持的最大比分数为 40。
2 实现
2.1 分析
很容易想到，比赛的可能路径可以使用如下的二叉树来分析，红色节点表示为不可能的分支
本例中的算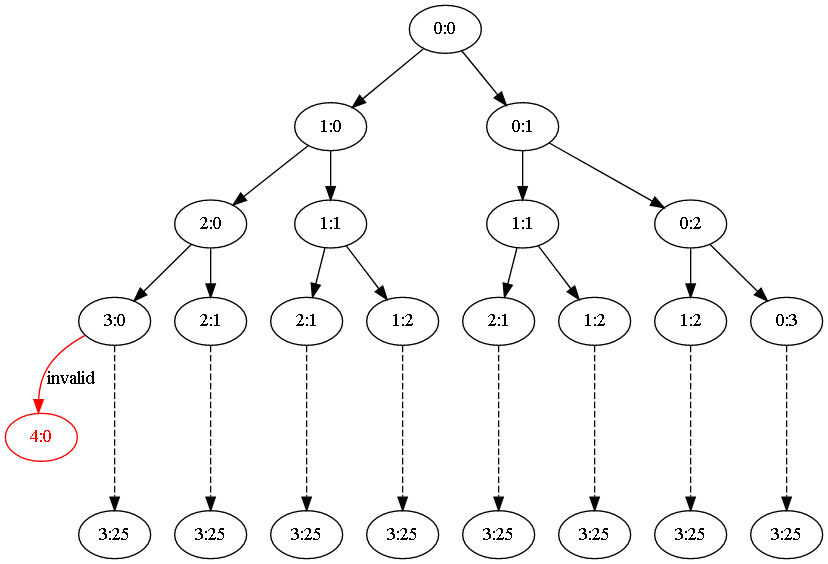
法使用 C# 实现
首先不管算法如何，先把一些公共的判断函数写在这里，以后其它例子都会用
// 是否有效最终比分
const int MAX = 25;
static bool IsValid(int A, int B)
{
if (A < MAX && B < MAX)
{
return false;
}
if (Math.Abs(A - B) < 2)
{
return false;
}
if (Math.Max(A, B) > MAX && Math.Abs(A - B) != 2)
{
return false;
}
return true;
}
// 是否为有效中间比分，例如如果最终比分为 3:25，中间不可能出现 2:25（已经赢了不用再打了）
static bool IsValidPath(int A, int B, int finalA, int finalB)
{
if (A > finalA || B > finalB)
{
return false;
}
if (IsWinStatus(A, B))
{
return A == finalA && B == finalB;
}
else
{
return true;
}
}
// 是否获胜
static bool IsWinStatus(int A, int B)
{
if (Math.Max(A, B) == MAX && Math.Abs(A - B) >= 2)
{
return true;
}
if (Math.Max(A, B) > MAX && Math.Abs(A - B) == 2)
{
return true;
}
return false;
}
2.2 算法一
很容易想到第一种算法，就是试图生成上图中的二叉树，如果生成出一个最终叶子结点（例如 3:25）则将计数器加 1，如下所示
class Model1
{
static void Main(string[] args)
{
int a = CalcScore1(7, 25);
Console.WriteLine("Result: " + a);
Console.Read();
}
// 计算可能得分的入口函数
static int CalcScore1(int A, int B)
{
if (!IsValid(A, B))
{
return 0;
}
Node rootNode = new Node(0, 0);
int counter = 0;
Constuct(rootNode, A, B, ref counter);
return counter;
}
private static void Constuct(Node node, int finalA, int finalB, ref int counter)
{
if (node.ValueA == finalA && node.ValueB == finalB)
{
counter++;
}
else
{
if (node.ValueA < finalA && IsValidPath(node.ValueA + 1, node.ValueB, finalA, finalB))
{
node.Left = new Node(node.ValueA + 1, node.ValueB);
}
if (node.ValueB < finalB && IsValidPath(node.ValueA, node.ValueB + 1, finalA, finalB))
{
node.Right = new Node(node.ValueA, node.ValueB + 1);
}
}
if (node.Left != null)
{
Constuct(node.Left, finalA, finalB, ref counter);
}
if (node.Right != null)
{
Constuct(node.Right, finalA, finalB, ref counter);
}
}
class Node
{
public Node(int A, int B)
{
this.ValueA = A;
this.ValueB = B;
}
public int ValueA { get; set; }
public int ValueB { get; set; }
public Node Left { get; set; }
public Node Right {